第4章 相似三角形 单元检测基础过关卷(含解析)
文档属性
| 名称 | 第4章 相似三角形 单元检测基础过关卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-17 09:08:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第4章 相似三角形 单元检测基础过关卷
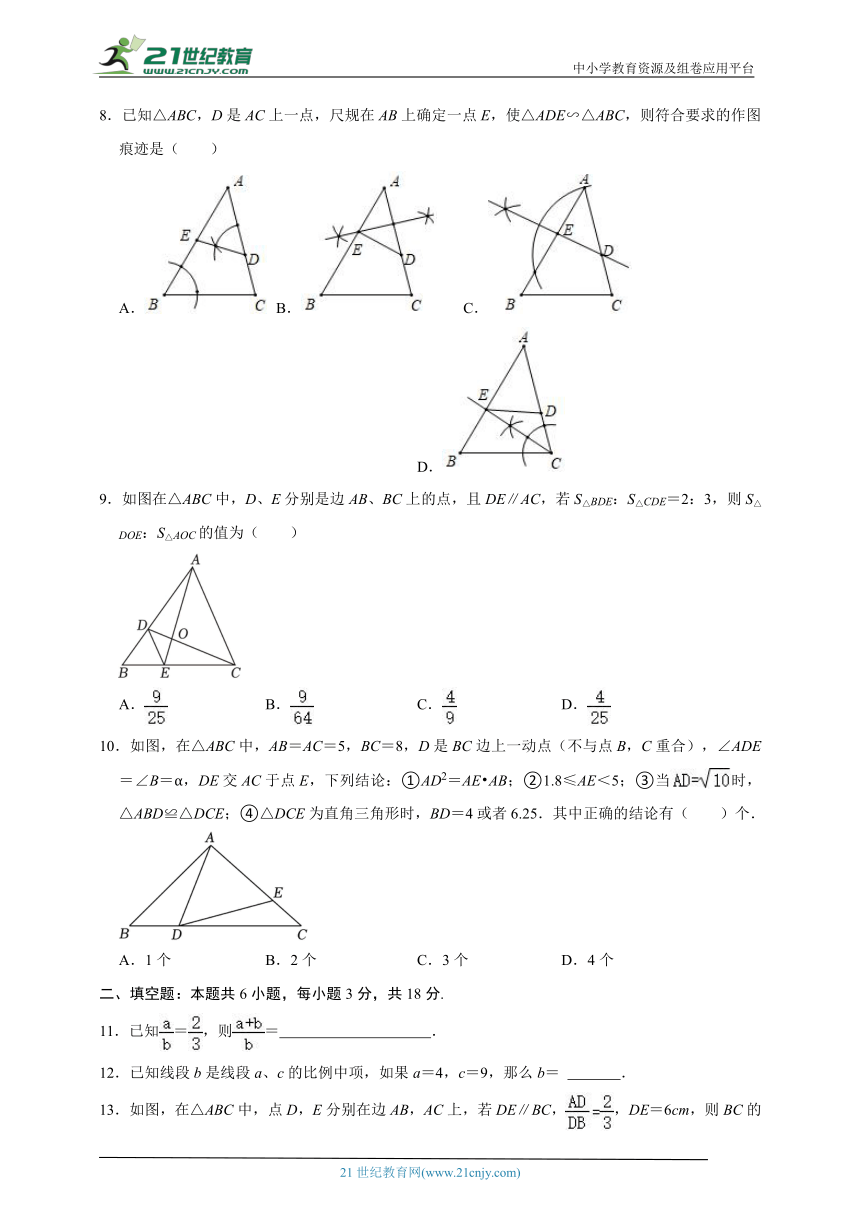
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.如图,已知直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3.若AB=4,AC=6,DF=9,则EF=( )
A.3 B.6 C.4 D.5
3.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C.D.
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若C(1,3),则点F的坐标是( )
A.(2,6) B.(2.5,4.5) C.(3,9) D.(4,8)
5.把矩形ABCD对折,折痕为MN,且矩形DMNC与矩形ABCD相似,则矩形ABCD的长AD与宽AB的比为( )
A.1: B.1: C.:1 D.:1
6.如图,是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=9m,则树高AB为( )
A.4m B.4.5m C.5m D.6m
8.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B. C. D.
9.如图在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=2:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
10.如图,在△ABC中,AB=AC=5,BC=8,D是BC边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:①AD2=AE AB;②1.8≤AE<5;③当时,△ABD≌△DCE;④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共6小题,每小题3分,共18分.
11.已知=,则= .
12.已知线段b是线段a、c的比例中项,如果a=4,c=9,那么b= .
13.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,,DE=6cm,则BC的长为 cm.
14.如图,在△ABC中,DE∥BC,AD:DB=1:2,△ADE的面积为1,则△BCD的面积为 .
15.如图,面积为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=BC,则小正方形的边长为 .
16.如图,在△ABC中,点D,E分别在边AB,AC上,且,,射线ED和CB的延长线交于点F,则的值为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)若AD=2DB,AE=4,AC=9,求BD的长.
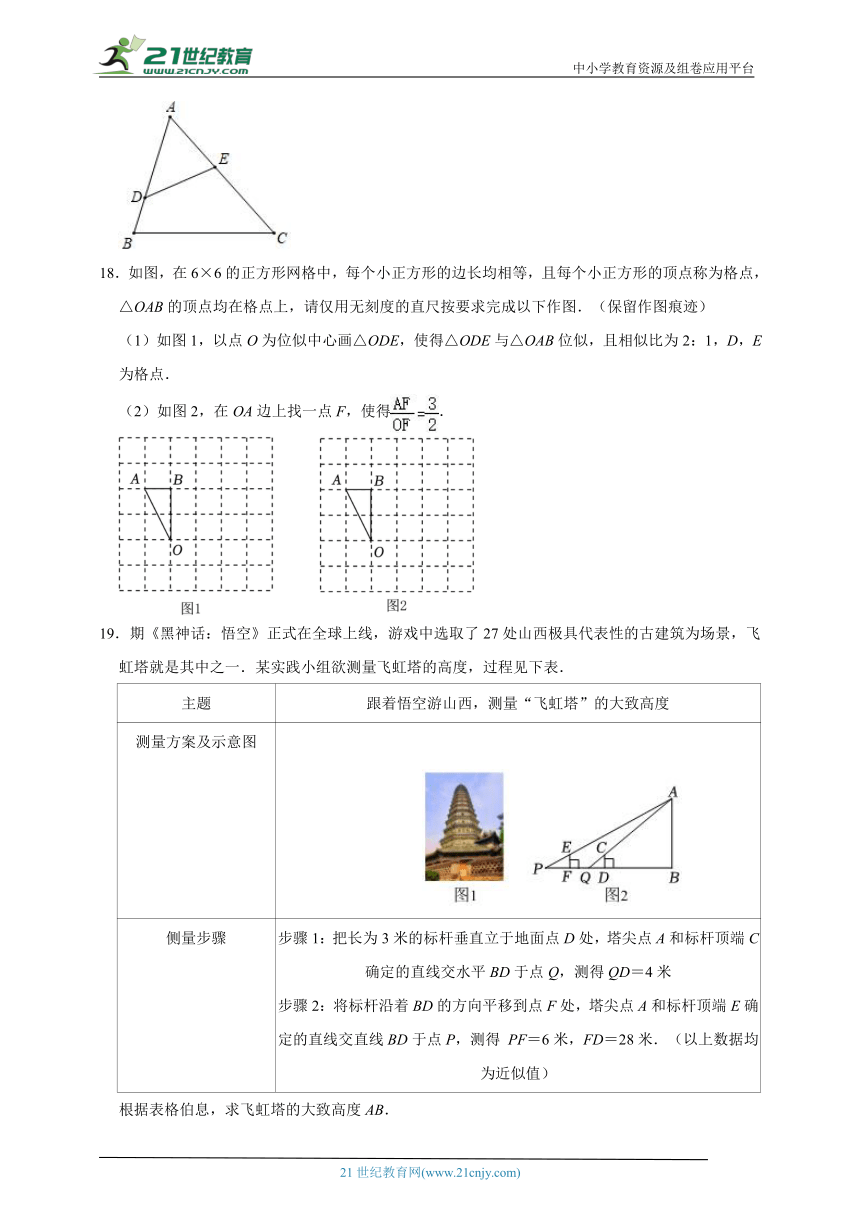
18.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2:1,D,E为格点.
(2)如图2,在OA边上找一点F,使得.
19.期《黑神话:悟空》正式在全球上线,游戏中选取了27处山西极具代表性的古建筑为场景,飞虹塔就是其中之一.某实践小组欲测量飞虹塔的高度,过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
侧量步骤 步骤1:把长为3米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平BD于点Q,测得QD=4米步骤2:将标杆沿着BD的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线BD于点P,测得 PF=6米,FD=28米.(以上数据均为近似值)
根据表格伯息,求飞虹塔的大致高度AB.
20.如图,在△ABC中,D是BC上的点,E是AD上一点,且,∠BAD=∠ECA.
(1)求证:AC2=BC CD;
(2)若AD是△ABC的中线,求的值.
21.如图,AB是⊙O的直径,点D是的中点,CD与BA的延长线交于E,BD与AC交于点F.
(1)求证:DC2=DF DB;
(2)若AE=AO,CD=2,求ED的长.
22.如图,在Rt△ABC中,∠B=90°,AB=8cm,BC=6cm.点P从A点出发沿AC向C点运动,速度为每秒2cm,同时点Q从C点出发沿CB向B点运动,速度为每秒1cm,当点P到达顶点C时,P、Q同时停止运动,设P点运动时间为t秒.
(1)当t为何值时,△PQC的面积为5cm2?
(2)当t为何值时,点P、C、Q组成的三角形与△ABC相似?
23.如图,在△ABC中,AB=AC=5cm,BC=8cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:=;
(2)当点P为BC中点时,求CM的值;
(3)当MP⊥BC时,求BP的值.
24.如图,在正方形ABCD中,点E为边CD上一动点,AE交BD于点F,过点F作FG⊥AE交BC于G点,点H为FG的中点.
(1)求证:AF=FG;
(2)若DE=DF,求证:FG2=CE CD;
(3)若DE=CE,求证:CG=2BG.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
【点拨】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【解析】解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
【点睛】此题考查了比例线段,根据成比例线段的概念,注意在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.同时注意单位要统一.
2.如图,已知直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3.若AB=4,AC=6,DF=9,则EF=( )
A.3 B.6 C.4 D.5
【点拨】先由l1∥l2∥l3,运用平行线分线段成比例的内容可得,再将AB=4,AC=6,DF=9代入求出DE,即可求解.
【解析】解:∵l1∥l2∥l3,AB=4,AC=6,DF=9,
∴,即,
解得DE=6.
∴EF=DF﹣DE=9﹣6=3.
故选:A.
【点睛】本题主要考查了平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
3.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.C.D.
【点拨】根据相似三角形的判定定理对各选项进行逐一判定即可.
【解析】解:A、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
B、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,
故本选项符合题意;
D、阴影三角形中,∠A的两边分别为6﹣2=4,8﹣5=3,则两三角形对应边成比例且夹角相等,故两三角形相似,
故本选项不符合题意.
故选:C.
【点睛】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若C(1,3),则点F的坐标是( )
A.(2,6) B.(2.5,4.5) C.(3,9) D.(4,8)
【点拨】根据点A、D的坐标求出相似比,再根据位似变换的性质计算,得到答案.
【解析】解:∵△ABC与△DEF位似,A(1.5,0),D(4.5,0),
∴△ABC与△DEF的相似比为1:3,
∵点C的坐标为(1,3),
∴点F的坐标为(1×3,3×3),即(3,9),
故选:C.
【点睛】本题考查的是位似变换,根据点A、D的坐标求出相似比是解题的关键.
5.把矩形ABCD对折,折痕为MN,且矩形DMNC与矩形ABCD相似,则矩形ABCD的长AD与宽AB的比为( )
A.1: B.1: C.:1 D.:1
【点拨】设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
【解析】解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴=,即=
即y2=x2.
∴x:y=:1.故选D.
【点睛】本题主要考查了相似多边形的对应边的比相等,注意分清对应边是解决本题的关键.
6.如图,是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
【点拨】根据黄金分割点列一元二次方程求解,然后根据矩形的性质即可解答.
【解析】解:由题意可得:BE2=2(2﹣BE),
解得:或(舍去).
故选:B.
【点睛】本题主要考查黄金分割点、矩形的性质,能根据黄金分割点列一元二次方程是解题的关键.
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=9m,则树高AB为( )
A.4m B.4.5m C.5m D.6m
【点拨】先判定△DEF和△DBC相似,然后根据相似三角形对应边成比例列式求出BC的长,再加上AC即可得解.
【解析】解:∵∠D=∠D,∠DEF=∠DCB,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4.5,
∵AC=1.5m,
∴AB=AC+BC=1.5+4.5=6(m),
即树高6m.
故选:D.
【点睛】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,比较简单,判定出△DEF和△DBC相似是解题的关键.
8.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B. C. D.
【点拨】以DA为边、点D为顶点在△ABC内部作一个角等于∠B,角的另一边与AB的交点即为所求作的点.
【解析】解:如图,点E即为所求作的点.
故选:A.
【点睛】本题主要考查作图﹣相似变换,根据相似三角形的判定明确过点D作一角等于∠B或∠C,并熟练掌握做一个角等于已知角的作法式解题的关键.
9.如图在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=2:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
【点拨】由BE:EC=2:3,求证△BDE∽△BAC,△DOE∽△COA,根据相似三角形性质得到,进而由相似三角形的性质即可解决问题.
【解析】解:过D作DF⊥BC,如图所示:
∴,,
∵S△BDE:S△CDE=2:3,
∴BE:EC=2:3,
∴BE:BC=2:5,
∵DE∥AC,
∴△BDE∽△BAC,△DOE∽△COA,
∴,
∴,
故选:D.
【点睛】本题主要考查了相似三角形的判定与性质,解题的关键是灵活运用相似三角形的判定及其性质来分析、判断、推理或解答.
10.如图,在△ABC中,AB=AC=5,BC=8,D是BC边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:①AD2=AE AB;②1.8≤AE<5;③当时,△ABD≌△DCE;④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
【点拨】如图1:在线段DE上取点F,使AF=AE,连接AF,易证△ABD∽△ADF进而可得AD2=AB AE即可判定①;结合①的结论可得,再确定AD的范围为3≤AD<5,进而得到1.8≤AE<5,即②正确;分两种情况:当BD<4时,可证明结论正确,当BD>4时,结论不成立;故③错误;△DCE为直角三角形,可分两种情况∠CDE=90°或∠CED=90°分别讨论求解即可④.
【解析】解:如图1,在线段 DE上取点F,使AF=AE,连接AF,则∠AFE=∠AEF
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B=a,
∴∠C=∠ADE=a,
∵∠AFE=∠DAF+∠ADE,∠AEF=∠C+∠CDE,
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
∴∠DAF=∠BAD,
∴△ABD∽△ADF,
∴,即AD2=AB AF
∴AD2=AB AE,故①正确;
∴,
当AD⊥BC时,由勾股定理可得:,
∴3≤AD<5,
∴,即1.8≤AE<5,故②正确;
如图2,作AH⊥BC于H,
∵AB=AC=5,
∴,
∴,
∵,
∴,
∴BD=3或BD′=5,CD=5或CD′=3,
∵∠BAD+∠B=∠ADC=∠ADE+∠CDE,∠ADE=∠B=a,
∴∠BAD=∠CDE,
∵∠B=∠C,DC=AB,
∴△ABD≌△DCE(SAS),
但△ABD′与△D′CE显然不是全等形,故③不正确;
如图3,AD⊥BC,DE⊥AC,
∴∠ADE+∠DAE=∠C+∠DAE=90°,
∴∠ADE=∠C=∠B,
∴BD=4,
如图4,DE⊥BC于D,AH⊥BC于H,
∵∠ADE=∠C,
∴∠ADH=∠CAH,
∴△ADH∽△CAH,
∴,即,
∴,
∴,故④正确.
故选C.
【点睛】本题主要考查了直角三角形性质、勾股定理、全等三角形判定和性质、相似三角形判定和性质、动点问题和分类讨论思想等知识点;掌握动点问题和分类讨论思想是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.已知=,则= .
【点拨】直接利用合比性质计算.
【解析】解:∵=,
∴==.
故答案为:.
【点睛】本题考查了比例的性质:熟练掌握比例的基本性质(内项之积等于外项之积、合比性质、分比性质、合分比性质、等比性质等)是解决问题的关键.
12.已知线段b是线段a、c的比例中项,如果a=4,c=9,那么b= 6 .
【点拨】根据比例中项的定义可得b2=ac,从而即可得到b的值.
【解析】解:∵线段b是线段a、c的比例中项,a=3、c=4,
∴b2=ac=4×9=36,
∴b=±6,
∵b>0,
∴b=6,
故答案为:6.
【点睛】本题考查了比例线段,解题的关键是理解比例中项的含义.
13.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,,DE=6cm,则BC的长为 15 cm.
【点拨】根据DE∥BC得△ADE∽△ABC,再根据相似三角形对应边成比例即可求解.
【解析】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵,
∴,
∴,
∵DE=6cm,
∴BC=15cm,
故答案为:15.
【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.
14.如图,在△ABC中,DE∥BC,AD:DB=1:2,△ADE的面积为1,则△BCD的面积为 6 .
【点拨】由AD:DB=1:2,推导出AD=AB,由DE∥BC证明△ADE∽△ABC,得==,则=,==,求得S△ADC=3,S△ABC=9,所以S△BCD=6,于是得到问题的答案.
【解析】解:∵AD:DB=1:2,
∴AD=AB=AB,
∵DE∥BC,△ADE的面积为1,
∴△ADE∽△ABC,
∴==,
∴=,===,
∴S△ADC=3S△ADE=3×1=3,S△ABC=9S△ADE=9×1=9,
∴S△BCD=S△ABC﹣S△ADC=9﹣3=6,
故答案为:6.
【点睛】此题重点考查相似三角形的判定与性质、“高相等的三角形的面积的比等于底边长的比”等知识,证明△ADE∽△ABC是解题的关键.
15.如图,面积为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=BC,则小正方形的边长为 .
【点拨】根据正方形的性质和相似三角形的判定,可以得到BE和CD的关系,BE和CF的关系,再根据正方形ABCD的面积为12,即可求得BE和BF的长,然后根据勾股定理即可求得EF的长.
【解析】解:∵四边形ABCD是正方形,四边形EFGH是正方形,
∴∠B=∠C=90°,BC=CD,∠EFG=90°,
∴∠EFB+∠FEB=90°,∠EFB+∠DFC=90°,
∴∠FEB=∠DFC,
∴△EBF∽△FCD,
∴,
∵BF=BC,
∴,
∴=,
∵正方形ABCD的面积为12,
∴正方形ABCD的边长为=2,
∴BC=CD=2,
∴BF=,
∴CF=,
∴BE=,
∴EF===,
故答案为:.
【点睛】本题考查相似三角形的判定与性质、正方形的性质、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.
16.如图,在△ABC中,点D,E分别在边AB,AC上,且,,射线ED和CB的延长线交于点F,则的值为 .
【点拨】过点B作BH∥EF交AC于H,根据平行线分线段成比例定理求出,进而求出=,再根据平行线分线段成比例定理计算即可.
【解析】解:过点B作BH∥EF交AC于H,
则==,
∵=,
∴=,
∵BH∥EF,
∴==,
故答案为:.
【点睛】本题考查的是平行线分线段成比例定理,正确作出辅助线、灵活运用定理是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)若AD=2DB,AE=4,AC=9,求BD的长.
【点拨】(1)根据相似三角形的判定即可求出证.
(2)设BD=x,则AD=2x,AB=3x,根据相似三角形的性质可知=,从而列出方程解出x的值.
【解析】(1)证明:∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)解:由(1)可知:△ADE∽△ACB,
∴=,
设BD=x,则AD=2x,AB=3x,
∵AE=4,AC=9,
∴=,
解得:x=(负值舍去),
∴BD的长是.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.
18.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2:1,D,E为格点.
(2)如图2,在OA边上找一点F,使得.
【点拨】(1)在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接OD,OE,DE,根据位似图形的判定和性质可知△ODE即为所求作;
(2)在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,根据相似三角形的判定和性质可知F即为所求.
【解析】解:(1)如图1所示,在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接OD,OE,DE,
则,
∵∠DOE=∠AOB,
∴△ODE∽△OAB,
故△ODE即为所求;
(2)如图2所示,在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,
则△AGF∽△OBF,
∵OB=2,
∴,
故点F即为所求作.
【点睛】本题主要考查了网格作图——位似变换,相似变换,熟练掌握位似三角形的判定与性质,相似三角形的判定与性质是解题的关键.
19.期《黑神话:悟空》正式在全球上线,游戏中选取了27处山西极具代表性的古建筑为场景,飞虹塔就是其中之一.某实践小组欲测量飞虹塔的高度,过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
侧量步骤 步骤1:把长为3米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平BD于点Q,测得QD=4米步骤2:将标杆沿着BD的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线BD于点P,测得 PF=6米,FD=28米.(以上数据均为近似值)
根据表格伯息,求飞虹塔的大致高度AB.
【点拨】判定△QCD∽△QAB,PEF∽△PAB,推出CD:AB=QD:QB,EF:AB=PF:PB,得到QD:QB=PF:PB,因此4:(4+BD)=6:(6+28+BD),求出BD=56米,得到3:AB=4:(4+56),即可求出AB=45米.
【解析】解:∵CD⊥PB,AB⊥PB,
∴CD∥AB,
∴△QCD∽△QAB,
同理:PEF∽△PAB,
∴CD:AB=QD:QB,EF:AB=PF:PB,
∵EF=CD,
∴QD:QB=PF:PB,
∵QD=4米,PF=6米,FD=28米,
∴4:(4+BD)=6:(6+28+BD),
∴BD=56米,
∴3:AB=4:(4+56),
∴AB=45米,
∴飞虹塔的大致高度是45米.
【点睛】本题考查相似三角形的应用,关键是判定△QCD∽△QAB,PEF∽△PAB,推出CD:AB=QD:QB,EF:AB=PF:PB,得到关于BD的方程.
20.如图,在△ABC中,D是BC上的点,E是AD上一点,且,∠BAD=∠ECA.
(1)求证:AC2=BC CD;
(2)若AD是△ABC的中线,求的值.
【点拨】(1)首先利用相似三角形的判定得出△BAD∽△ACE进而求出△ABC∽△DAC,再利用相似三角形的性质得出答案即可;
(2)由三角形的外角性质可得:∠ADC=∠B+∠BAD,∠CED=∠CAE+∠ECA,可证得∠ADC=∠CED,则有CE=CD,再结合(1)的结论,以及AD是△ABC的中线,即可求解.
【解析】证明:(1)∵,∠BAD=∠ECA,
∴△BAD∽△ACE,
∴∠B=∠EAC,
∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴,
∴AC2=BC CD;
(2)∵∠ADC是△ABD的外角,∠CED是△ACE的外角,
∴∠ADC=∠B+∠BAD,∠CED=∠CAE+∠ECA,
由(1)可知,∠B=∠EAC,∠BAD=∠ECA,
∴∠ADC=∠CED,
∴CE=CD,
∵AD是△ABC的中线,
∴BC=2CD,
∴BC=2CE,
由(1)得:AC2=BC CD,
∴AC2=2CE CE,
∴,
即.
【点睛】本题主要考查相似三角形的判定与性质,根据已知得出△BAD∽△ACE是解题关键.
21.如图,AB是⊙O的直径,点D是的中点,CD与BA的延长线交于E,BD与AC交于点F.
(1)求证:DC2=DF DB;
(2)若AE=AO,CD=2,求ED的长.
【点拨】(1)由点D是的中点,得到∠ABD=∠CBD,等量代换得到∠ACD=∠CBD,根据相似三角形的性质即可得到结论;
(2)连接OD,如图,根据等腰三角形的性质得到∠OBD=∠ODB,等量代换得到∠ODB=∠CBD,根据平行线的判定得到OD∥BC,于是得到结论.
【解析】(1)证明:∵点D是的中点,
∴∠ABD=∠CBD,
而∠ABD=∠ACD,
∴∠ACD=∠CBD,
∵∠BDC=∠CDF,
∴△CDF∽△BDC,
∴=,
即DC2=DF DB;
(2)解:连接OD,如图,
∵OD=OB,
∴∠OBD=∠ODB,
而∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∴=,
∵EA=AO=BO,
∴=,
∴ED=4.
【点睛】本题考查了相似三角形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.
22.如图,在Rt△ABC中,∠B=90°,AB=8cm,BC=6cm.点P从A点出发沿AC向C点运动,速度为每秒2cm,同时点Q从C点出发沿CB向B点运动,速度为每秒1cm,当点P到达顶点C时,P、Q同时停止运动,设P点运动时间为t秒.
(1)当t为何值时,△PQC的面积为5cm2?
(2)当t为何值时,点P、C、Q组成的三角形与△ABC相似?
【点拨】(1)首先作出高线,由平行线分线段成比例定理得出比例式,由含有t的代数式表示出PD的长度,再根据三角形的面积公式得出即可.
(2)根据已知条件需要分类讨论,分两种情况讨论,从而得出比例式,代入即可求出.
【解析】解:(1)如图1中,过点P作PD⊥BC于点D,
∵∠B=90°,
∴AB∥PD,
∴=,
∴PD===,
∴S△PQC= CQ PD=t =5,
∴t1=t2=;
(3)如图2中,当△PQC∽△ABC时,
∴=,
∴=,
∴t=.
当△PQC∽△BAC 时,
∴=,
∴=,
∴t=,
综上所述,t=或时,△PQC与△ABC 相似.
【点睛】本题是三角形动点问题,考查了勾股定理,等腰三角形,三角形的面积,相似三角形的性及分类讨论的数学思想,解题关键是能用t表示相关的线段的长度.
23.如图,在△ABC中,AB=AC=5cm,BC=8cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:=;
(2)当点P为BC中点时,求CM的值;
(3)当MP⊥BC时,求BP的值.
【点拨】(1)由AB=AC得∠B=∠C,而∠APM=∠B,则∠BAP=180°﹣∠B﹣∠APB=180°﹣∠APM﹣∠APB=∠CPM,即可根据“两角分别相等的两个三角形相似”证明△BAP∽△CPM,得=;
(2)由点P为BC中点得BP=CP=BC=4cm,而AB=AC=5cm,由=得CM==cm;
(3)作AD⊥BC于点D,则BD=CD=BC=4cm,由∠BAP=∠BDA=90°,∠A=∠A,证明△BAP∽△BDA,即可根据“相似三角形的对应边成比例”求出BP的值.
【解析】(1)证明:如图1,∵AB=AC,
∴∠B=∠C,
∵∠APM=∠B,
∴∠BAP=180°﹣∠B﹣∠APB=180°﹣∠APM﹣∠APB=∠CPM,
∴△BAP∽△CPM,
∴=.
(2)解:如图2,∵AB=AC=5cm,BC=8cm,点P为BC中点,
∴BP=CP=BC=4cm,
由(1)得=,
∴CM===(cm).
(3)解:如图3,MP⊥BC,
作AD⊥BC于点D,则BD=CD=BC=4cm,
由(1)得∠BAP=∠CPM,
∵∠CPM=90°,
∴∠BAP=∠BDA=90°,
∵∠A=∠A,
∴△BAP∽△BDA,
∴=,
∴BP===(cm).
【点睛】此题重点考查等腰三角形的性质、三角形内角和定理、相似三角形的判定与性质等知识,证明△BAP∽△CPM是解题的关键.
24.如图,在正方形ABCD中,点E为边CD上一动点,AE交BD于点F,过点F作FG⊥AE交BC于G点,点H为FG的中点.
(1)求证:AF=FG;
(2)若DE=DF,求证:FG2=CE CD;
(3)若DE=CE,求证:CG=2BG.
【点拨】(1)连接EC,证明△ABF和△CBF全等,得AF=CF,∠BAF=∠BCF,在四边形ABGF中,由∠ABC=90°,FG⊥AE得∠BAF+∠BGF=180°,再根据∠FGC+∠BGF=180°得∠BAF=∠FGC,则∠BCF=∠FGC,进而得FG=CF,由此即可得出结论;
(2)根据∠CDF=45°,DE=DF得∠DEF=∠DFE=67.5°,进而得∠FCE=22.5°,∠CFE=45°,则∠CFE=∠CDF=45°,由此得△FCE∽△DCF,则CF:CD=CE:CF,即CF2=CE CD,然后再根据FG=CF即可得出结论;
(3)过点F作FM⊥BC,MF的延长线交AD于N,则四边形CDNM为矩形,进而得DN=CM,根据FG=CF,FM⊥BC得CM=GM=DN,则CG=2GM,证明△DFE∽△BFA得DF:BF=DE:AB=2:1,再证明△DNF∽△BMF得DN:BM=DF:BF=2:1,则BM=2DN,即BG+GM=2GM,由此得BG=GM,据此即可得出结论.
【解析】证明:(1)连接EC,如图1所示:
∵四边形ABCD为正方形,
∴AB=CB,∠ABF=∠CBF=45°,∠ABC=90°,
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
在四边形ABGF中,∠ABC=90°,FG⊥AE,
∴∠BAF+∠BGF=180°,
又∵∠FGC+∠BGF=180°,
∴∠BAF=∠FGC,
∴∠BCF=∠FGC,
∴FG=CF,
∴AF=FG;
(2)∵四边形ABCD为正方形,
∴∠CDF=45°,∠ADC=90°,
∵DE=DF,
∴∠DEF=∠DFE=(180°﹣∠BDC)=67.5°,
∴∠DAE=90°﹣∠DEF=22.5°,
∴∠BAF=∠BCF=90°﹣22.5°=67.5°,
∴∠FCE=90°﹣∠BCF=22.5°,
∵∠DEF=∠FCE+∠CFE,
∴∠CFE=∠DEF﹣∠FCE=67.5°﹣22.5°=45°,
∴∠CFE=∠CDF=45°,
又∵∠FCE=∠DCF,
∴△FCE∽△DCF,
∴CF:CD=CE:CF,
∴CF2=CE CD,
∵FG=CF,
∴FG2=CE CD;
(3)过点F作FM⊥BC,MF的延长线交AD于N,如图2所示:
∵四边形ABCD为正方形,
∴∠ADC=∠DCB=90°,AB=CD,AD∥BC,AB∥CD,
∵MN⊥BC,
∴四边形CDNM为矩形,
∴DN=CM,
∴FG=CF,FM⊥BC,
∴CM=GM=DN,
∴CG=2GM
∵DE=CE,
∴DE=CD=AB,
即DE:AB=1:2,
∵AB∥CD,
∴△DFE∽△BFA,
∴DF:BF=DE:AB=1:2,
∵AD∥BC,
∴△DNF∽△BMF,
∴DN:BM=DF:BF=1:2,
∴BM=2DN,
即BG+GM=2GM,
∴BG=GM,
∴CG=2GM=2BG.
【点睛】此题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质,理解正方形的性质,熟练掌握相似三角形的判定与性质,全等三角形的判定与性质是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第4章 相似三角形 单元检测基础过关卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
2.如图,已知直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3.若AB=4,AC=6,DF=9,则EF=( )
A.3 B.6 C.4 D.5
3.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B. C.D.
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若C(1,3),则点F的坐标是( )
A.(2,6) B.(2.5,4.5) C.(3,9) D.(4,8)
5.把矩形ABCD对折,折痕为MN,且矩形DMNC与矩形ABCD相似,则矩形ABCD的长AD与宽AB的比为( )
A.1: B.1: C.:1 D.:1
6.如图,是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=9m,则树高AB为( )
A.4m B.4.5m C.5m D.6m
8.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B. C. D.
9.如图在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=2:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
10.如图,在△ABC中,AB=AC=5,BC=8,D是BC边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:①AD2=AE AB;②1.8≤AE<5;③当时,△ABD≌△DCE;④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
二、填空题:本题共6小题,每小题3分,共18分.
11.已知=,则= .
12.已知线段b是线段a、c的比例中项,如果a=4,c=9,那么b= .
13.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,,DE=6cm,则BC的长为 cm.
14.如图,在△ABC中,DE∥BC,AD:DB=1:2,△ADE的面积为1,则△BCD的面积为 .
15.如图,面积为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=BC,则小正方形的边长为 .
16.如图,在△ABC中,点D,E分别在边AB,AC上,且,,射线ED和CB的延长线交于点F,则的值为 .
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)若AD=2DB,AE=4,AC=9,求BD的长.
18.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2:1,D,E为格点.
(2)如图2,在OA边上找一点F,使得.
19.期《黑神话:悟空》正式在全球上线,游戏中选取了27处山西极具代表性的古建筑为场景,飞虹塔就是其中之一.某实践小组欲测量飞虹塔的高度,过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
侧量步骤 步骤1:把长为3米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平BD于点Q,测得QD=4米步骤2:将标杆沿着BD的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线BD于点P,测得 PF=6米,FD=28米.(以上数据均为近似值)
根据表格伯息,求飞虹塔的大致高度AB.
20.如图,在△ABC中,D是BC上的点,E是AD上一点,且,∠BAD=∠ECA.
(1)求证:AC2=BC CD;
(2)若AD是△ABC的中线,求的值.
21.如图,AB是⊙O的直径,点D是的中点,CD与BA的延长线交于E,BD与AC交于点F.
(1)求证:DC2=DF DB;
(2)若AE=AO,CD=2,求ED的长.
22.如图,在Rt△ABC中,∠B=90°,AB=8cm,BC=6cm.点P从A点出发沿AC向C点运动,速度为每秒2cm,同时点Q从C点出发沿CB向B点运动,速度为每秒1cm,当点P到达顶点C时,P、Q同时停止运动,设P点运动时间为t秒.
(1)当t为何值时,△PQC的面积为5cm2?
(2)当t为何值时,点P、C、Q组成的三角形与△ABC相似?
23.如图,在△ABC中,AB=AC=5cm,BC=8cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:=;
(2)当点P为BC中点时,求CM的值;
(3)当MP⊥BC时,求BP的值.
24.如图,在正方形ABCD中,点E为边CD上一动点,AE交BD于点F,过点F作FG⊥AE交BC于G点,点H为FG的中点.
(1)求证:AF=FG;
(2)若DE=DF,求证:FG2=CE CD;
(3)若DE=CE,求证:CG=2BG.
答案与解析
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下面四组线段中,成比例的是( )
A.a=2,b=3,c=4,d=5 B.a=1,b=2,c=2,d=4
C.a=4,b=6,c=8,d=10 D.a=,b=,c=3,d=
【点拨】如果其中两条线段的乘积等于另外两条线段的乘积,则四条线段叫成比例线段.对选项一一分析,排除错误答案.
【解析】解:A、2×5≠3×4,故选项不符合题意;
B、1×4=2×2,故选项符合题意;
C、4×10≠6×8,故选项不符合题意;
D、×3≠×,故选项不符合题意.
故选:B.
【点睛】此题考查了比例线段,根据成比例线段的概念,注意在相乘的时候,最小的和最大的相乘,另外两个相乘,看它们的积是否相等.同时注意单位要统一.
2.如图,已知直线l1,l2,l3分别交直线l4于点A,B,C,交直线l5于点D,E,F,且l1∥l2∥l3.若AB=4,AC=6,DF=9,则EF=( )
A.3 B.6 C.4 D.5
【点拨】先由l1∥l2∥l3,运用平行线分线段成比例的内容可得,再将AB=4,AC=6,DF=9代入求出DE,即可求解.
【解析】解:∵l1∥l2∥l3,AB=4,AC=6,DF=9,
∴,即,
解得DE=6.
∴EF=DF﹣DE=9﹣6=3.
故选:A.
【点睛】本题主要考查了平行线分线段成比例,掌握平行线分线段成比例是解题的关键.
3.如图,△ABC中,∠A=76°,AB=8,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
A. B.C.D.
【点拨】根据相似三角形的判定定理对各选项进行逐一判定即可.
【解析】解:A、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
B、阴影三角形与原三角形有两个角相等,故两三角形相似,
故本选项不符合题意;
C、两三角形的对应边不成比例,故两三角形不相似,
故本选项符合题意;
D、阴影三角形中,∠A的两边分别为6﹣2=4,8﹣5=3,则两三角形对应边成比例且夹角相等,故两三角形相似,
故本选项不符合题意.
故选:C.
【点睛】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此题的关键.
4.如图,在平面直角坐标系中,已知A(1.5,0),D(4.5,0),△ABC与△DEF位似,原点O是位似中心.若C(1,3),则点F的坐标是( )
A.(2,6) B.(2.5,4.5) C.(3,9) D.(4,8)
【点拨】根据点A、D的坐标求出相似比,再根据位似变换的性质计算,得到答案.
【解析】解:∵△ABC与△DEF位似,A(1.5,0),D(4.5,0),
∴△ABC与△DEF的相似比为1:3,
∵点C的坐标为(1,3),
∴点F的坐标为(1×3,3×3),即(3,9),
故选:C.
【点睛】本题考查的是位似变换,根据点A、D的坐标求出相似比是解题的关键.
5.把矩形ABCD对折,折痕为MN,且矩形DMNC与矩形ABCD相似,则矩形ABCD的长AD与宽AB的比为( )
A.1: B.1: C.:1 D.:1
【点拨】设矩形ABCD的长AD=x,宽AB=y,根据相似多边形对应边的比相等,即可求得.
【解析】解:设矩形ABCD的长AD=x,宽AB=y,则DM=AD=x.
∵矩形DMNC与矩形ABCD相似.
∴=,即=
即y2=x2.
∴x:y=:1.故选D.
【点睛】本题主要考查了相似多边形的对应边的比相等,注意分清对应边是解决本题的关键.
6.如图,是著名画家达芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内,点E是AB的黄金分割点,BE>AE,若AB=2,则BE长为( )
A. B. C. D.
【点拨】根据黄金分割点列一元二次方程求解,然后根据矩形的性质即可解答.
【解析】解:由题意可得:BE2=2(2﹣BE),
解得:或(舍去).
故选:B.
【点睛】本题主要考查黄金分割点、矩形的性质,能根据黄金分割点列一元二次方程是解题的关键.
7.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上,已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度AC=1.5m,CD=9m,则树高AB为( )
A.4m B.4.5m C.5m D.6m
【点拨】先判定△DEF和△DBC相似,然后根据相似三角形对应边成比例列式求出BC的长,再加上AC即可得解.
【解析】解:∵∠D=∠D,∠DEF=∠DCB,
∴△DEF∽△DBC,
∴=,
即=,
解得:BC=4.5,
∵AC=1.5m,
∴AB=AC+BC=1.5+4.5=6(m),
即树高6m.
故选:D.
【点睛】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,比较简单,判定出△DEF和△DBC相似是解题的关键.
8.已知△ABC,D是AC上一点,尺规在AB上确定一点E,使△ADE∽△ABC,则符合要求的作图痕迹是( )
A. B. C. D.
【点拨】以DA为边、点D为顶点在△ABC内部作一个角等于∠B,角的另一边与AB的交点即为所求作的点.
【解析】解:如图,点E即为所求作的点.
故选:A.
【点睛】本题主要考查作图﹣相似变换,根据相似三角形的判定明确过点D作一角等于∠B或∠C,并熟练掌握做一个角等于已知角的作法式解题的关键.
9.如图在△ABC中,D、E分别是边AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=2:3,则S△DOE:S△AOC的值为( )
A. B. C. D.
【点拨】由BE:EC=2:3,求证△BDE∽△BAC,△DOE∽△COA,根据相似三角形性质得到,进而由相似三角形的性质即可解决问题.
【解析】解:过D作DF⊥BC,如图所示:
∴,,
∵S△BDE:S△CDE=2:3,
∴BE:EC=2:3,
∴BE:BC=2:5,
∵DE∥AC,
∴△BDE∽△BAC,△DOE∽△COA,
∴,
∴,
故选:D.
【点睛】本题主要考查了相似三角形的判定与性质,解题的关键是灵活运用相似三角形的判定及其性质来分析、判断、推理或解答.
10.如图,在△ABC中,AB=AC=5,BC=8,D是BC边上一动点(不与点B,C重合),∠ADE=∠B=α,DE交AC于点E,下列结论:①AD2=AE AB;②1.8≤AE<5;③当时,△ABD≌△DCE;④△DCE为直角三角形时,BD=4或者6.25.其中正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
【点拨】如图1:在线段DE上取点F,使AF=AE,连接AF,易证△ABD∽△ADF进而可得AD2=AB AE即可判定①;结合①的结论可得,再确定AD的范围为3≤AD<5,进而得到1.8≤AE<5,即②正确;分两种情况:当BD<4时,可证明结论正确,当BD>4时,结论不成立;故③错误;△DCE为直角三角形,可分两种情况∠CDE=90°或∠CED=90°分别讨论求解即可④.
【解析】解:如图1,在线段 DE上取点F,使AF=AE,连接AF,则∠AFE=∠AEF
∵AB=AC,
∴∠B=∠C,
∵∠ADE=∠B=a,
∴∠C=∠ADE=a,
∵∠AFE=∠DAF+∠ADE,∠AEF=∠C+∠CDE,
∴∠DAF=∠CDE,
∵∠ADE+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
∴∠DAF=∠BAD,
∴△ABD∽△ADF,
∴,即AD2=AB AF
∴AD2=AB AE,故①正确;
∴,
当AD⊥BC时,由勾股定理可得:,
∴3≤AD<5,
∴,即1.8≤AE<5,故②正确;
如图2,作AH⊥BC于H,
∵AB=AC=5,
∴,
∴,
∵,
∴,
∴BD=3或BD′=5,CD=5或CD′=3,
∵∠BAD+∠B=∠ADC=∠ADE+∠CDE,∠ADE=∠B=a,
∴∠BAD=∠CDE,
∵∠B=∠C,DC=AB,
∴△ABD≌△DCE(SAS),
但△ABD′与△D′CE显然不是全等形,故③不正确;
如图3,AD⊥BC,DE⊥AC,
∴∠ADE+∠DAE=∠C+∠DAE=90°,
∴∠ADE=∠C=∠B,
∴BD=4,
如图4,DE⊥BC于D,AH⊥BC于H,
∵∠ADE=∠C,
∴∠ADH=∠CAH,
∴△ADH∽△CAH,
∴,即,
∴,
∴,故④正确.
故选C.
【点睛】本题主要考查了直角三角形性质、勾股定理、全等三角形判定和性质、相似三角形判定和性质、动点问题和分类讨论思想等知识点;掌握动点问题和分类讨论思想是解题的关键.
二、填空题:本题共6小题,每小题3分,共18分。
11.已知=,则= .
【点拨】直接利用合比性质计算.
【解析】解:∵=,
∴==.
故答案为:.
【点睛】本题考查了比例的性质:熟练掌握比例的基本性质(内项之积等于外项之积、合比性质、分比性质、合分比性质、等比性质等)是解决问题的关键.
12.已知线段b是线段a、c的比例中项,如果a=4,c=9,那么b= 6 .
【点拨】根据比例中项的定义可得b2=ac,从而即可得到b的值.
【解析】解:∵线段b是线段a、c的比例中项,a=3、c=4,
∴b2=ac=4×9=36,
∴b=±6,
∵b>0,
∴b=6,
故答案为:6.
【点睛】本题考查了比例线段,解题的关键是理解比例中项的含义.
13.如图,在△ABC中,点D,E分别在边AB,AC上,若DE∥BC,,DE=6cm,则BC的长为 15 cm.
【点拨】根据DE∥BC得△ADE∽△ABC,再根据相似三角形对应边成比例即可求解.
【解析】解:∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵,
∴,
∴,
∵DE=6cm,
∴BC=15cm,
故答案为:15.
【点睛】本题考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.
14.如图,在△ABC中,DE∥BC,AD:DB=1:2,△ADE的面积为1,则△BCD的面积为 6 .
【点拨】由AD:DB=1:2,推导出AD=AB,由DE∥BC证明△ADE∽△ABC,得==,则=,==,求得S△ADC=3,S△ABC=9,所以S△BCD=6,于是得到问题的答案.
【解析】解:∵AD:DB=1:2,
∴AD=AB=AB,
∵DE∥BC,△ADE的面积为1,
∴△ADE∽△ABC,
∴==,
∴=,===,
∴S△ADC=3S△ADE=3×1=3,S△ABC=9S△ADE=9×1=9,
∴S△BCD=S△ABC﹣S△ADC=9﹣3=6,
故答案为:6.
【点睛】此题重点考查相似三角形的判定与性质、“高相等的三角形的面积的比等于底边长的比”等知识,证明△ADE∽△ABC是解题的关键.
15.如图,面积为12的正方形ABCD中,有一个小正方形EFGH,其中E、F、G分别在AB、BC、FD上,若BF=BC,则小正方形的边长为 .
【点拨】根据正方形的性质和相似三角形的判定,可以得到BE和CD的关系,BE和CF的关系,再根据正方形ABCD的面积为12,即可求得BE和BF的长,然后根据勾股定理即可求得EF的长.
【解析】解:∵四边形ABCD是正方形,四边形EFGH是正方形,
∴∠B=∠C=90°,BC=CD,∠EFG=90°,
∴∠EFB+∠FEB=90°,∠EFB+∠DFC=90°,
∴∠FEB=∠DFC,
∴△EBF∽△FCD,
∴,
∵BF=BC,
∴,
∴=,
∵正方形ABCD的面积为12,
∴正方形ABCD的边长为=2,
∴BC=CD=2,
∴BF=,
∴CF=,
∴BE=,
∴EF===,
故答案为:.
【点睛】本题考查相似三角形的判定与性质、正方形的性质、勾股定理,解答本题的关键是明确题意,利用数形结合的思想解答.
16.如图,在△ABC中,点D,E分别在边AB,AC上,且,,射线ED和CB的延长线交于点F,则的值为 .
【点拨】过点B作BH∥EF交AC于H,根据平行线分线段成比例定理求出,进而求出=,再根据平行线分线段成比例定理计算即可.
【解析】解:过点B作BH∥EF交AC于H,
则==,
∵=,
∴=,
∵BH∥EF,
∴==,
故答案为:.
【点睛】本题考查的是平行线分线段成比例定理,正确作出辅助线、灵活运用定理是解题的关键.
三.解答题(共8小题,其中第17、18题每题6分,第19、20题每题8分,第21、22题每题10分,第23、24题每题12分,共72分)
17.如图,在△ABC中,D,E分别是边AB,AC上的点,连接DE,且∠ADE=∠ACB.
(1)求证:△ADE∽△ACB;
(2)若AD=2DB,AE=4,AC=9,求BD的长.
【点拨】(1)根据相似三角形的判定即可求出证.
(2)设BD=x,则AD=2x,AB=3x,根据相似三角形的性质可知=,从而列出方程解出x的值.
【解析】(1)证明:∵∠ADE=∠ACB,∠A=∠A,
∴△ADE∽△ACB;
(2)解:由(1)可知:△ADE∽△ACB,
∴=,
设BD=x,则AD=2x,AB=3x,
∵AE=4,AC=9,
∴=,
解得:x=(负值舍去),
∴BD的长是.
【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.
18.如图,在6×6的正方形网格中,每个小正方形的边长均相等,且每个小正方形的顶点称为格点,△OAB的顶点均在格点上,请仅用无刻度的直尺按要求完成以下作图.(保留作图痕迹)
(1)如图1,以点O为位似中心画△ODE,使得△ODE与△OAB位似,且相似比为2:1,D,E为格点.
(2)如图2,在OA边上找一点F,使得.
【点拨】(1)在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接OD,OE,DE,根据位似图形的判定和性质可知△ODE即为所求作;
(2)在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,根据相似三角形的判定和性质可知F即为所求.
【解析】解:(1)如图1所示,在OA延长线上取格点D,在OB延长线上取格点E,使OD=2OA,OE=2OB,连接OD,OE,DE,
则,
∵∠DOE=∠AOB,
∴△ODE∽△OAB,
故△ODE即为所求;
(2)如图2所示,在点A的下方取格点G,使AG=3,AG∥OB,连接BG交AO于点F,
则△AGF∽△OBF,
∵OB=2,
∴,
故点F即为所求作.
【点睛】本题主要考查了网格作图——位似变换,相似变换,熟练掌握位似三角形的判定与性质,相似三角形的判定与性质是解题的关键.
19.期《黑神话:悟空》正式在全球上线,游戏中选取了27处山西极具代表性的古建筑为场景,飞虹塔就是其中之一.某实践小组欲测量飞虹塔的高度,过程见下表.
主题 跟着悟空游山西,测量“飞虹塔”的大致高度
测量方案及示意图
侧量步骤 步骤1:把长为3米的标杆垂直立于地面点D处,塔尖点A和标杆顶端C确定的直线交水平BD于点Q,测得QD=4米步骤2:将标杆沿着BD的方向平移到点F处,塔尖点A和标杆顶端E确定的直线交直线BD于点P,测得 PF=6米,FD=28米.(以上数据均为近似值)
根据表格伯息,求飞虹塔的大致高度AB.
【点拨】判定△QCD∽△QAB,PEF∽△PAB,推出CD:AB=QD:QB,EF:AB=PF:PB,得到QD:QB=PF:PB,因此4:(4+BD)=6:(6+28+BD),求出BD=56米,得到3:AB=4:(4+56),即可求出AB=45米.
【解析】解:∵CD⊥PB,AB⊥PB,
∴CD∥AB,
∴△QCD∽△QAB,
同理:PEF∽△PAB,
∴CD:AB=QD:QB,EF:AB=PF:PB,
∵EF=CD,
∴QD:QB=PF:PB,
∵QD=4米,PF=6米,FD=28米,
∴4:(4+BD)=6:(6+28+BD),
∴BD=56米,
∴3:AB=4:(4+56),
∴AB=45米,
∴飞虹塔的大致高度是45米.
【点睛】本题考查相似三角形的应用,关键是判定△QCD∽△QAB,PEF∽△PAB,推出CD:AB=QD:QB,EF:AB=PF:PB,得到关于BD的方程.
20.如图,在△ABC中,D是BC上的点,E是AD上一点,且,∠BAD=∠ECA.
(1)求证:AC2=BC CD;
(2)若AD是△ABC的中线,求的值.
【点拨】(1)首先利用相似三角形的判定得出△BAD∽△ACE进而求出△ABC∽△DAC,再利用相似三角形的性质得出答案即可;
(2)由三角形的外角性质可得:∠ADC=∠B+∠BAD,∠CED=∠CAE+∠ECA,可证得∠ADC=∠CED,则有CE=CD,再结合(1)的结论,以及AD是△ABC的中线,即可求解.
【解析】证明:(1)∵,∠BAD=∠ECA,
∴△BAD∽△ACE,
∴∠B=∠EAC,
∵∠ACB=∠DCA,
∴△ABC∽△DAC,
∴,
∴AC2=BC CD;
(2)∵∠ADC是△ABD的外角,∠CED是△ACE的外角,
∴∠ADC=∠B+∠BAD,∠CED=∠CAE+∠ECA,
由(1)可知,∠B=∠EAC,∠BAD=∠ECA,
∴∠ADC=∠CED,
∴CE=CD,
∵AD是△ABC的中线,
∴BC=2CD,
∴BC=2CE,
由(1)得:AC2=BC CD,
∴AC2=2CE CE,
∴,
即.
【点睛】本题主要考查相似三角形的判定与性质,根据已知得出△BAD∽△ACE是解题关键.
21.如图,AB是⊙O的直径,点D是的中点,CD与BA的延长线交于E,BD与AC交于点F.
(1)求证:DC2=DF DB;
(2)若AE=AO,CD=2,求ED的长.
【点拨】(1)由点D是的中点,得到∠ABD=∠CBD,等量代换得到∠ACD=∠CBD,根据相似三角形的性质即可得到结论;
(2)连接OD,如图,根据等腰三角形的性质得到∠OBD=∠ODB,等量代换得到∠ODB=∠CBD,根据平行线的判定得到OD∥BC,于是得到结论.
【解析】(1)证明:∵点D是的中点,
∴∠ABD=∠CBD,
而∠ABD=∠ACD,
∴∠ACD=∠CBD,
∵∠BDC=∠CDF,
∴△CDF∽△BDC,
∴=,
即DC2=DF DB;
(2)解:连接OD,如图,
∵OD=OB,
∴∠OBD=∠ODB,
而∠OBD=∠CBD,
∴∠ODB=∠CBD,
∴OD∥BC,
∴=,
∵EA=AO=BO,
∴=,
∴ED=4.
【点睛】本题考查了相似三角形的判定和性质,圆周角定理,正确的作出辅助线是解题的关键.
22.如图,在Rt△ABC中,∠B=90°,AB=8cm,BC=6cm.点P从A点出发沿AC向C点运动,速度为每秒2cm,同时点Q从C点出发沿CB向B点运动,速度为每秒1cm,当点P到达顶点C时,P、Q同时停止运动,设P点运动时间为t秒.
(1)当t为何值时,△PQC的面积为5cm2?
(2)当t为何值时,点P、C、Q组成的三角形与△ABC相似?
【点拨】(1)首先作出高线,由平行线分线段成比例定理得出比例式,由含有t的代数式表示出PD的长度,再根据三角形的面积公式得出即可.
(2)根据已知条件需要分类讨论,分两种情况讨论,从而得出比例式,代入即可求出.
【解析】解:(1)如图1中,过点P作PD⊥BC于点D,
∵∠B=90°,
∴AB∥PD,
∴=,
∴PD===,
∴S△PQC= CQ PD=t =5,
∴t1=t2=;
(3)如图2中,当△PQC∽△ABC时,
∴=,
∴=,
∴t=.
当△PQC∽△BAC 时,
∴=,
∴=,
∴t=,
综上所述,t=或时,△PQC与△ABC 相似.
【点睛】本题是三角形动点问题,考查了勾股定理,等腰三角形,三角形的面积,相似三角形的性及分类讨论的数学思想,解题关键是能用t表示相关的线段的长度.
23.如图,在△ABC中,AB=AC=5cm,BC=8cm,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B.
(1)求证:=;
(2)当点P为BC中点时,求CM的值;
(3)当MP⊥BC时,求BP的值.
【点拨】(1)由AB=AC得∠B=∠C,而∠APM=∠B,则∠BAP=180°﹣∠B﹣∠APB=180°﹣∠APM﹣∠APB=∠CPM,即可根据“两角分别相等的两个三角形相似”证明△BAP∽△CPM,得=;
(2)由点P为BC中点得BP=CP=BC=4cm,而AB=AC=5cm,由=得CM==cm;
(3)作AD⊥BC于点D,则BD=CD=BC=4cm,由∠BAP=∠BDA=90°,∠A=∠A,证明△BAP∽△BDA,即可根据“相似三角形的对应边成比例”求出BP的值.
【解析】(1)证明:如图1,∵AB=AC,
∴∠B=∠C,
∵∠APM=∠B,
∴∠BAP=180°﹣∠B﹣∠APB=180°﹣∠APM﹣∠APB=∠CPM,
∴△BAP∽△CPM,
∴=.
(2)解:如图2,∵AB=AC=5cm,BC=8cm,点P为BC中点,
∴BP=CP=BC=4cm,
由(1)得=,
∴CM===(cm).
(3)解:如图3,MP⊥BC,
作AD⊥BC于点D,则BD=CD=BC=4cm,
由(1)得∠BAP=∠CPM,
∵∠CPM=90°,
∴∠BAP=∠BDA=90°,
∵∠A=∠A,
∴△BAP∽△BDA,
∴=,
∴BP===(cm).
【点睛】此题重点考查等腰三角形的性质、三角形内角和定理、相似三角形的判定与性质等知识,证明△BAP∽△CPM是解题的关键.
24.如图,在正方形ABCD中,点E为边CD上一动点,AE交BD于点F,过点F作FG⊥AE交BC于G点,点H为FG的中点.
(1)求证:AF=FG;
(2)若DE=DF,求证:FG2=CE CD;
(3)若DE=CE,求证:CG=2BG.
【点拨】(1)连接EC,证明△ABF和△CBF全等,得AF=CF,∠BAF=∠BCF,在四边形ABGF中,由∠ABC=90°,FG⊥AE得∠BAF+∠BGF=180°,再根据∠FGC+∠BGF=180°得∠BAF=∠FGC,则∠BCF=∠FGC,进而得FG=CF,由此即可得出结论;
(2)根据∠CDF=45°,DE=DF得∠DEF=∠DFE=67.5°,进而得∠FCE=22.5°,∠CFE=45°,则∠CFE=∠CDF=45°,由此得△FCE∽△DCF,则CF:CD=CE:CF,即CF2=CE CD,然后再根据FG=CF即可得出结论;
(3)过点F作FM⊥BC,MF的延长线交AD于N,则四边形CDNM为矩形,进而得DN=CM,根据FG=CF,FM⊥BC得CM=GM=DN,则CG=2GM,证明△DFE∽△BFA得DF:BF=DE:AB=2:1,再证明△DNF∽△BMF得DN:BM=DF:BF=2:1,则BM=2DN,即BG+GM=2GM,由此得BG=GM,据此即可得出结论.
【解析】证明:(1)连接EC,如图1所示:
∵四边形ABCD为正方形,
∴AB=CB,∠ABF=∠CBF=45°,∠ABC=90°,
在△ABF和△CBF中,
,
∴△ABF≌△CBF(SAS),
∴AF=CF,∠BAF=∠BCF,
在四边形ABGF中,∠ABC=90°,FG⊥AE,
∴∠BAF+∠BGF=180°,
又∵∠FGC+∠BGF=180°,
∴∠BAF=∠FGC,
∴∠BCF=∠FGC,
∴FG=CF,
∴AF=FG;
(2)∵四边形ABCD为正方形,
∴∠CDF=45°,∠ADC=90°,
∵DE=DF,
∴∠DEF=∠DFE=(180°﹣∠BDC)=67.5°,
∴∠DAE=90°﹣∠DEF=22.5°,
∴∠BAF=∠BCF=90°﹣22.5°=67.5°,
∴∠FCE=90°﹣∠BCF=22.5°,
∵∠DEF=∠FCE+∠CFE,
∴∠CFE=∠DEF﹣∠FCE=67.5°﹣22.5°=45°,
∴∠CFE=∠CDF=45°,
又∵∠FCE=∠DCF,
∴△FCE∽△DCF,
∴CF:CD=CE:CF,
∴CF2=CE CD,
∵FG=CF,
∴FG2=CE CD;
(3)过点F作FM⊥BC,MF的延长线交AD于N,如图2所示:
∵四边形ABCD为正方形,
∴∠ADC=∠DCB=90°,AB=CD,AD∥BC,AB∥CD,
∵MN⊥BC,
∴四边形CDNM为矩形,
∴DN=CM,
∴FG=CF,FM⊥BC,
∴CM=GM=DN,
∴CG=2GM
∵DE=CE,
∴DE=CD=AB,
即DE:AB=1:2,
∵AB∥CD,
∴△DFE∽△BFA,
∴DF:BF=DE:AB=1:2,
∵AD∥BC,
∴△DNF∽△BMF,
∴DN:BM=DF:BF=1:2,
∴BM=2DN,
即BG+GM=2GM,
∴BG=GM,
∴CG=2GM=2BG.
【点睛】此题主要考查了相似三角形的判定与性质,全等三角形的判定与性质,正方形的性质,理解正方形的性质,熟练掌握相似三角形的判定与性质,全等三角形的判定与性质是解决问题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
