1.3 证明(2) 同步练习(含答案)
文档属性
| 名称 | 1.3 证明(2) 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 285.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-24 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.3 证明(2)
1.一个三角形至少有( ).
A.一个锐角 B.两个锐角 C.一个钝角 D.一个直角
2.已知在△ABC中,∠A:∠B:∠C=2:3:4,则这个三角形是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.如图所示,AD,AE分别为△ABC的高线和角平分线,且∠B=76°,∠C=36°,则∠DAE的度数为( ).
A.20° B.18° C.38° D.40°
4.如图所示,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB 上一点.将Rt△ABC沿CD折叠,使点 B 落在AC 边上的点B'处,则∠ADB'等于( ).
A.40° B.35° C.30° D.25°
5.如图所示,已知AD平分∠BAC交BC于点D,CE⊥AD于点E,∠B=26°,∠DCE=34°,则∠BAC的度数为 .
6.如图所示,P是△ABC内一点,∠ABC=80°,∠1=∠2,则∠BPC= .
7.如图所示,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E.请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
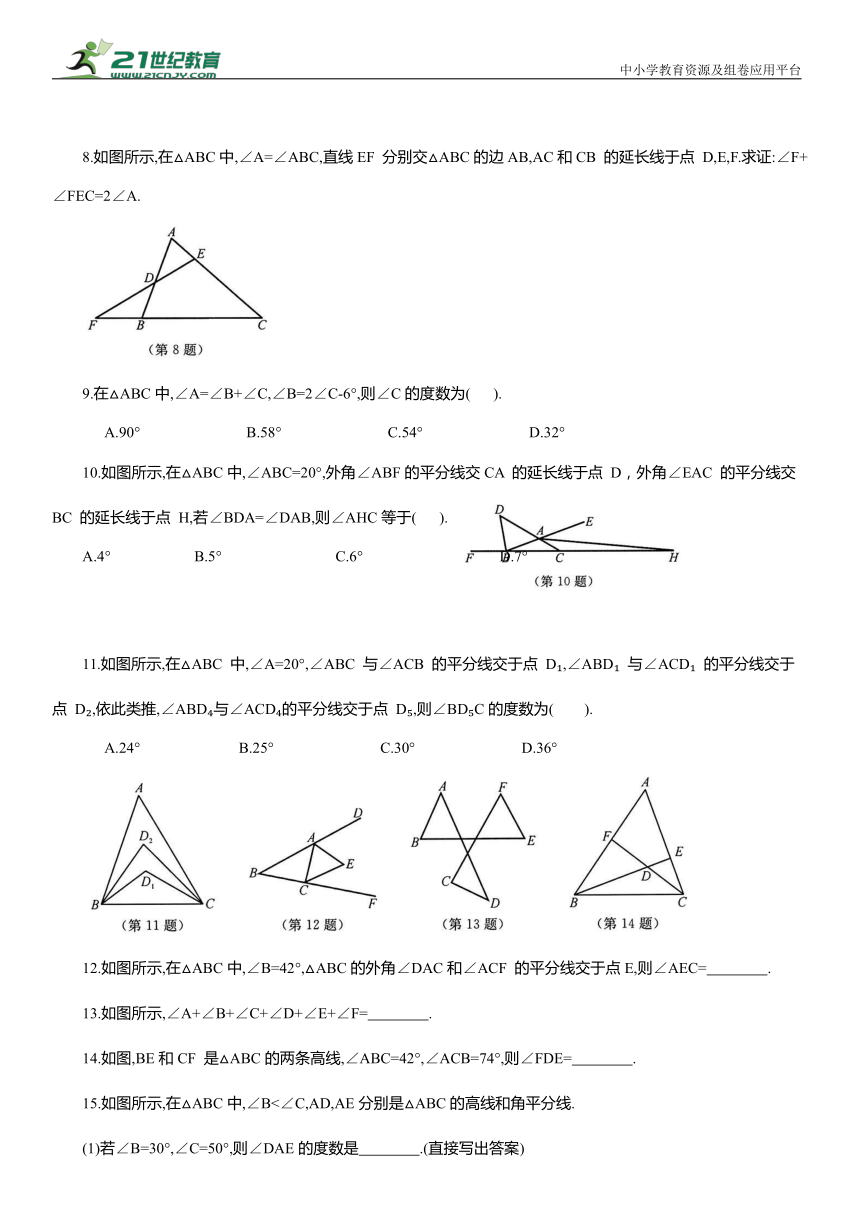
8.如图所示,在△ABC中,∠A=∠ABC,直线EF 分别交△ABC的边AB,AC和CB 的延长线于点 D,E,F.求证:∠F+∠FEC=2∠A.
9.在△ABC中,∠A=∠B+∠C,∠B=2∠C-6°,则∠C的度数为( ).
A.90° B.58° C.54° D.32°
10.如图所示,在△ABC中,∠ABC=20°,外角∠ABF的平分线交CA 的延长线于点 D,外角∠EAC 的平分线交BC 的延长线于点 H,若∠BDA=∠DAB,则∠AHC等于( ).
A.4° B.5° C.6° D.7°
11.如图所示,在△ABC 中,∠A=20°,∠ABC 与∠ACB 的平分线交于点 D ,∠ABD 与∠ACD 的平分线交于点 D ,依此类推,∠ABD 与∠ACD 的平分线交于点 D ,则∠BD C的度数为( ).
A.24° B.25° C.30° D.36°
12.如图所示,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF 的平分线交于点E,则∠AEC= .
13.如图所示,∠A+∠B+∠C+∠D+∠E+∠F= .
14.如图,BE和CF 是△ABC的两条高线,∠ABC=42°,∠ACB=74°,则∠FDE= .
15.如图所示,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高线和角平分线.
(1)若∠B=30°,∠C=50°,则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE,∠B,∠C的数量关系: ,并证明你的结论.
16.证明命题“三角形的两条内角平分线所夹的锐角与第三个内角的一半互余”是真命题.
17.将一副三角尺按如图所示摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( ).
A.15° B.20° C.25° D.30°
18.将一副三角尺按如图所示摆放,则∠α与∠β的数量关系为( ).
A.∠α+∠β=180°B.∠α+∠β=225° C.∠α+∠β=270° D.∠α=∠β
19.(1)如图1所示,把△ABC纸片沿DE 折叠,使点A 落在四边形BCED 的内部点A'的位置,试说明2∠A=∠1+∠2.
(2)如图2所示,若把△ABC纸片沿DE 折叠,使点A 落在四边形BCED 的外部点A'的位置,此时∠A 与∠1,∠2之间的数量关系是 .
(3)如图3所示,若把四边形ABCD沿EF 折叠,使点 A,D落在四边形 BCFE的内部点A',D'的位置,请你探索此时∠A,∠D,∠1与∠2之间的数量关系,写出你的结论并说明理由.
1.3 证明(2)
1. B 2. A 3. A 4. A 5.60° 6.100°
7.①若AB∥DE,BC∥EF,则∠B=∠E,此命题为真命题;
②若AB∥DE,∠B=∠E,则 BC∥EF,此命题为真命题;
③若∠B=∠E,BC∥EF,则AB∥DE,此命题为真命题.
以①为例证明如下:
∵AB∥DE,∴∠B=∠DOC.
∵BC∥EF,∴∠DOC=∠E.∴∠B=∠E.
8.∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,∴∠F+∠FEC=∠F+∠A+∠ADE.
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC.
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
9. D 10. B 11. B 12.69° 13.360°14.116°
15.(1)10° (2)∠DAE= (∠C-∠B)
证明:∵AD是△ABC的高,∴∠ADC=90°.
∴∠DAC=180°-∠ADC-∠C=90°-∠C.
∵AE是△ABC的角平分线,
∴∠DAE=∠EAC-∠DAC
16.已知:AD,BE,CF 是△ABC的角平分线,如答图所示.
求证:∠1+∠2=90°.
证明:∵AD,BE,CF是△ABC的角平分线,
即命题“三角形的两条内角平分线所夹的锐角与第三个内角的一半互余”是真命题.
17. A 18. B
19.(1)根据翻折的性质, ∠AED=180°,
∴2∠A=∠1+∠2.
(2)2∠A=∠1-∠2
(3)2(∠A+∠D)=∠1+∠2+360°.理由如下:根据翻折的性质,
∵∠A+∠D+∠AEF+∠DFE=360°,∴∠A+
∴2(∠A+∠D)=∠1+∠2+360°.
1.3 证明(2)
1.一个三角形至少有( ).
A.一个锐角 B.两个锐角 C.一个钝角 D.一个直角
2.已知在△ABC中,∠A:∠B:∠C=2:3:4,则这个三角形是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
3.如图所示,AD,AE分别为△ABC的高线和角平分线,且∠B=76°,∠C=36°,则∠DAE的度数为( ).
A.20° B.18° C.38° D.40°
4.如图所示,在Rt△ACB中,∠ACB=90°,∠A=25°,D是AB 上一点.将Rt△ABC沿CD折叠,使点 B 落在AC 边上的点B'处,则∠ADB'等于( ).
A.40° B.35° C.30° D.25°
5.如图所示,已知AD平分∠BAC交BC于点D,CE⊥AD于点E,∠B=26°,∠DCE=34°,则∠BAC的度数为 .
6.如图所示,P是△ABC内一点,∠ABC=80°,∠1=∠2,则∠BPC= .
7.如图所示,已知BC,DE相交于点O,给出以下三个判断:①AB∥DE;②BC∥EF;③∠B=∠E.请你以其中两个判断作为条件,另外一个判断作为结论,写出所有的命题,指出这些命题是真命题还是假命题,并选择其中的一个真命题加以证明.
8.如图所示,在△ABC中,∠A=∠ABC,直线EF 分别交△ABC的边AB,AC和CB 的延长线于点 D,E,F.求证:∠F+∠FEC=2∠A.
9.在△ABC中,∠A=∠B+∠C,∠B=2∠C-6°,则∠C的度数为( ).
A.90° B.58° C.54° D.32°
10.如图所示,在△ABC中,∠ABC=20°,外角∠ABF的平分线交CA 的延长线于点 D,外角∠EAC 的平分线交BC 的延长线于点 H,若∠BDA=∠DAB,则∠AHC等于( ).
A.4° B.5° C.6° D.7°
11.如图所示,在△ABC 中,∠A=20°,∠ABC 与∠ACB 的平分线交于点 D ,∠ABD 与∠ACD 的平分线交于点 D ,依此类推,∠ABD 与∠ACD 的平分线交于点 D ,则∠BD C的度数为( ).
A.24° B.25° C.30° D.36°
12.如图所示,在△ABC中,∠B=42°,△ABC的外角∠DAC和∠ACF 的平分线交于点E,则∠AEC= .
13.如图所示,∠A+∠B+∠C+∠D+∠E+∠F= .
14.如图,BE和CF 是△ABC的两条高线,∠ABC=42°,∠ACB=74°,则∠FDE= .
15.如图所示,在△ABC中,∠B<∠C,AD,AE分别是△ABC的高线和角平分线.
(1)若∠B=30°,∠C=50°,则∠DAE的度数是 .(直接写出答案)
(2)写出∠DAE,∠B,∠C的数量关系: ,并证明你的结论.
16.证明命题“三角形的两条内角平分线所夹的锐角与第三个内角的一半互余”是真命题.
17.将一副三角尺按如图所示摆放,点E在AC上,点D在BC的延长线上,EF∥BC,∠B=∠EDF=90°,∠A=45°,∠F=60°,则∠CED的度数是( ).
A.15° B.20° C.25° D.30°
18.将一副三角尺按如图所示摆放,则∠α与∠β的数量关系为( ).
A.∠α+∠β=180°B.∠α+∠β=225° C.∠α+∠β=270° D.∠α=∠β
19.(1)如图1所示,把△ABC纸片沿DE 折叠,使点A 落在四边形BCED 的内部点A'的位置,试说明2∠A=∠1+∠2.
(2)如图2所示,若把△ABC纸片沿DE 折叠,使点A 落在四边形BCED 的外部点A'的位置,此时∠A 与∠1,∠2之间的数量关系是 .
(3)如图3所示,若把四边形ABCD沿EF 折叠,使点 A,D落在四边形 BCFE的内部点A',D'的位置,请你探索此时∠A,∠D,∠1与∠2之间的数量关系,写出你的结论并说明理由.
1.3 证明(2)
1. B 2. A 3. A 4. A 5.60° 6.100°
7.①若AB∥DE,BC∥EF,则∠B=∠E,此命题为真命题;
②若AB∥DE,∠B=∠E,则 BC∥EF,此命题为真命题;
③若∠B=∠E,BC∥EF,则AB∥DE,此命题为真命题.
以①为例证明如下:
∵AB∥DE,∴∠B=∠DOC.
∵BC∥EF,∴∠DOC=∠E.∴∠B=∠E.
8.∵∠FEC=∠A+∠ADE,∠F+∠BDF=∠ABC,∴∠F+∠FEC=∠F+∠A+∠ADE.
∵∠ADE=∠BDF,
∴∠F+∠FEC=∠A+∠ABC.
∵∠A=∠ABC,
∴∠F+∠FEC=∠A+∠ABC=2∠A.
9. D 10. B 11. B 12.69° 13.360°14.116°
15.(1)10° (2)∠DAE= (∠C-∠B)
证明:∵AD是△ABC的高,∴∠ADC=90°.
∴∠DAC=180°-∠ADC-∠C=90°-∠C.
∵AE是△ABC的角平分线,
∴∠DAE=∠EAC-∠DAC
16.已知:AD,BE,CF 是△ABC的角平分线,如答图所示.
求证:∠1+∠2=90°.
证明:∵AD,BE,CF是△ABC的角平分线,
即命题“三角形的两条内角平分线所夹的锐角与第三个内角的一半互余”是真命题.
17. A 18. B
19.(1)根据翻折的性质, ∠AED=180°,
∴2∠A=∠1+∠2.
(2)2∠A=∠1-∠2
(3)2(∠A+∠D)=∠1+∠2+360°.理由如下:根据翻折的性质,
∵∠A+∠D+∠AEF+∠DFE=360°,∴∠A+
∴2(∠A+∠D)=∠1+∠2+360°.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
