专题复习二 勾股定理的综合应用 同步练习(含答案)-2024-2025学年浙教版八年级数学上册
文档属性
| 名称 | 专题复习二 勾股定理的综合应用 同步练习(含答案)-2024-2025学年浙教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 402.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-25 15:41:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习二 勾股定理的综合应用
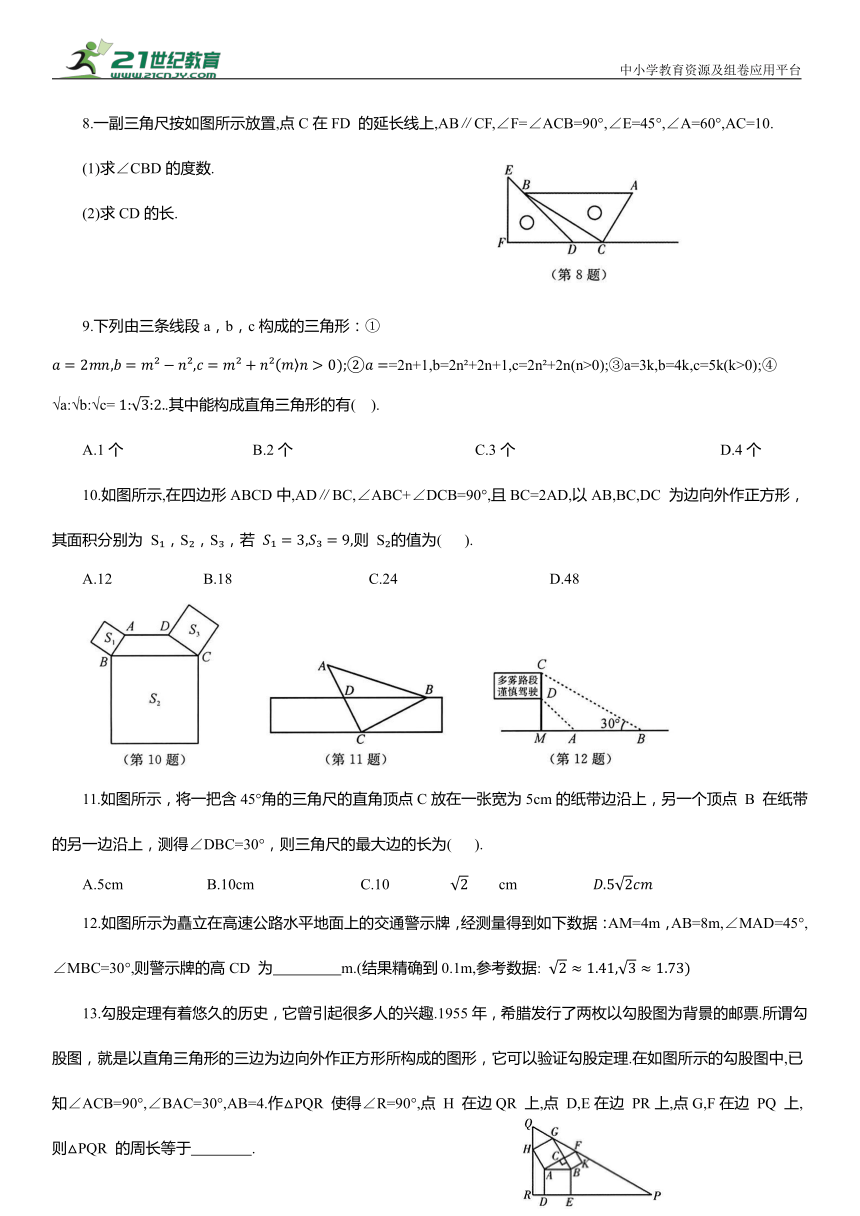
1.如图所示,折叠直角三角形纸片△ABC,使点C落在斜边AB 上的点E 处,已知AB=8 ,∠B=30°,则 DE 的长为( ).
A.4 B.6
2.如图所示,图中所有三角形都是直角三角形,所有四边形都是正方形,已知 则S的值为( ).
A.25 B.31 C.32 D.40
3.如图所示,要制作底边 BC长为44cm,顶点A 到BC的距离与BC长的比为1:4的等腰三角形木衣架,则腰AB 的长至少为 cm.(结果保留根号)
4.在△ABC中,AB=15cm,AC=13cm,高线AD=12cm,则△ABC的周长是 cm.
5.将一副三角尺按如图所示的方式叠放在一起,若AB=20cm,则阴影部分的面积是 cm .
6.如图所示为一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其长方形平板面ABCD的宽AB 为1m,若要想顺利推过(不可竖起来或侧翻)直角走廊,则平板车的长AD不能超过 m.
7.如图所示,在△ABC中,AC=6,BC=8,DE是△ABD的边AB 上的高,且DE=4,AD= 求△ABC 的边AB 上的高.
8.一副三角尺按如图所示放置,点C在FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.
(1)求∠CBD的度数.
(2)求CD的长.
9.下列由三条线段a,b,c构成的三角形:① =2n+1,b=2n +2n+1,c=2n +2n(n>0);③a=3k,b=4k,c=5k(k>0);④√a:√b:√c= .其中能构成直角三角形的有( ).
A.1个 B.2个 C.3个 D.4个
10.如图所示,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB,BC,DC 为边向外作正方形,其面积分别为 S ,S ,S ,若 则 S 的值为( ).
A.12 B.18 C.24 D.48
11.如图所示,将一把含45°角的三角尺的直角顶点C放在一张宽为5cm的纸带边沿上,另一个顶点 B 在纸带的另一边沿上,测得∠DBC=30°,则三角尺的最大边的长为( ).
A.5cm B.10cm C.10 cm
12.如图所示为矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4m,AB=8m,∠MAD=45°,∠MBC=30°,则警示牌的高CD 为 m.(结果精确到0.1m,参考数据:
13.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年,希腊发行了两枚以勾股图为背景的邮票.所谓勾股图,就是以直角三角形的三边为边向外作正方形所构成的图形,它可以验证勾股定理.在如图所示的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR 使得∠R=90°,点 H 在边QR 上,点 D,E在边 PR上,点G,F在边 PQ 上,则△PQR 的周长等于 .
14.【探究】如图1所示,分别以△ABC的两边AB,AC为边向△ABC外作正三角形ABD 和正三角形ACE,连结DC,BE,求证:DC=BE.
【拓展】如图 2所示,在四边形 ABCD 中,AB=BC=5,∠ABC=45°,连结 AC,BD,若∠DAC=90°,AC=AD,求 BD的长.
15.问题背景:
在△ABC中,已知AB,BC,AC三边的长分别为 ,求这个三角形的面积.
小辉在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不用求△ABC的高线长,借用网格就能计算出它的面积.我们把上述求△ABC 面积的方法叫做构图法.
(1)若△ABC三边的长分别为 请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
思维拓展:
(2)若△ABC三边的长分别为 且 m≠n),试运用构图法求出这个三角形的面积.
探索创新:
(3)已知a,b都是正数,a+b=3,求当a,b为何值时, 有最小值,并求出这个最小值.
16.【广西】《九章算术》是古代东方数学代表作,书中记载:今有开门去阔(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1,2所示(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点 D 距离门槛AB 都为1尺(1尺=10寸),则 AB的长是( ).
A.50.5寸 B.52寸 C.101寸 D.104寸
17.如图所示,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
18.如图所示,在△ABC中,∠BAC=90°,AB专题复习二 勾股定理的综合应用
1. A 2. B 3.11 4.42 或32 5.50
7.∵DE是AB边上的高,∴∠AED=∠BED=90°.在 Rt △ADE 中, 由 勾 股 定 理, 得 AE =
同理,在 Rt△BDE中,由勾股定理,得 BE=8,∴AB=2+8=10.
在△ABC中,由AB=10,AC=6,BC=8,得AB =AC +BC ,∴△ABC是直角三角形.
设△ABC的AB 边上的高为h,
则 即10h=6×8,∴h=4.8.
8.(1)∵∠F=90°,∠E=45°,∴∠EDF=45°.
∵∠ACB=90°,∠A=60°,∴∠ABC=30°.
∵AB∥CF,∴∠ABD=∠EDF=45°.
∴∠CBD=∠ABD-∠ABC=15°.
(2)如答图所示,过点 B 作 BM⊥FD于点 M.
∵∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°.∴AB=20.
∵AB∥CF,∴∠BCM=30°.
由(1)知∠EDF=45°.∴MD=BM=5
∴CD=CM-MD=15-5
9. C 10. D11. C 12.2.9
14.【探究】∵以AB,AC为边分别向外作正三角形ABD 和正三角形ACE,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°.
∴∠DAB+∠BAC=∠EAC+∠BAC.
∴∠DAC=∠BAE.
在△DAC和△BAE中, ∴△DAC≌△BAE(SAS).∴DC=BE.
【拓展】如答图所示,以 AB 为边向 外 作 等 腰 直 角 三 角 形ABE,AE=AB,∠BAE=90°,∴∠BAD=∠EAC.
在△AEC和△ABD中,
∴△AEC≌△ABD.∴CE=BD.
15.(1)图略.
(3)如答图所示,构造AB=2,DE=5,BD=3,AB⊥BD,DE⊥BD,当A,C,E三点在同一条直线上时,AC+CE最小.过点A作AF∥BD,交 ED的延长线于点 F.
∴EF=AB+DE=7,AF=BD=3.
∴AC+CE的最小值是
的最小值是
16. C
17.设 BD=x,则CD=14-x.
在 Rt△ABD中,
在 Rt△ACD 中, 解得x=9.
∴AD=12.
证明:延长QM至点D,使MD=MQ,连结 PD,BD,BQ,CD.
在△CMQ和△BMD中,∵
∴△CMQ≌△BMD.
∴CQ=BD,∠QCM=∠DBM.
∴CQ∥BD.又∵∠BAC=90°.∴∠PBD=90°.
∵PM垂直平分DQ,∴PQ=PD.
专题复习二 勾股定理的综合应用
1.如图所示,折叠直角三角形纸片△ABC,使点C落在斜边AB 上的点E 处,已知AB=8 ,∠B=30°,则 DE 的长为( ).
A.4 B.6
2.如图所示,图中所有三角形都是直角三角形,所有四边形都是正方形,已知 则S的值为( ).
A.25 B.31 C.32 D.40
3.如图所示,要制作底边 BC长为44cm,顶点A 到BC的距离与BC长的比为1:4的等腰三角形木衣架,则腰AB 的长至少为 cm.(结果保留根号)
4.在△ABC中,AB=15cm,AC=13cm,高线AD=12cm,则△ABC的周长是 cm.
5.将一副三角尺按如图所示的方式叠放在一起,若AB=20cm,则阴影部分的面积是 cm .
6.如图所示为一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其长方形平板面ABCD的宽AB 为1m,若要想顺利推过(不可竖起来或侧翻)直角走廊,则平板车的长AD不能超过 m.
7.如图所示,在△ABC中,AC=6,BC=8,DE是△ABD的边AB 上的高,且DE=4,AD= 求△ABC 的边AB 上的高.
8.一副三角尺按如图所示放置,点C在FD 的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10.
(1)求∠CBD的度数.
(2)求CD的长.
9.下列由三条线段a,b,c构成的三角形:① =2n+1,b=2n +2n+1,c=2n +2n(n>0);③a=3k,b=4k,c=5k(k>0);④√a:√b:√c= .其中能构成直角三角形的有( ).
A.1个 B.2个 C.3个 D.4个
10.如图所示,在四边形ABCD中,AD∥BC,∠ABC+∠DCB=90°,且BC=2AD,以AB,BC,DC 为边向外作正方形,其面积分别为 S ,S ,S ,若 则 S 的值为( ).
A.12 B.18 C.24 D.48
11.如图所示,将一把含45°角的三角尺的直角顶点C放在一张宽为5cm的纸带边沿上,另一个顶点 B 在纸带的另一边沿上,测得∠DBC=30°,则三角尺的最大边的长为( ).
A.5cm B.10cm C.10 cm
12.如图所示为矗立在高速公路水平地面上的交通警示牌,经测量得到如下数据:AM=4m,AB=8m,∠MAD=45°,∠MBC=30°,则警示牌的高CD 为 m.(结果精确到0.1m,参考数据:
13.勾股定理有着悠久的历史,它曾引起很多人的兴趣.1955年,希腊发行了两枚以勾股图为背景的邮票.所谓勾股图,就是以直角三角形的三边为边向外作正方形所构成的图形,它可以验证勾股定理.在如图所示的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQR 使得∠R=90°,点 H 在边QR 上,点 D,E在边 PR上,点G,F在边 PQ 上,则△PQR 的周长等于 .
14.【探究】如图1所示,分别以△ABC的两边AB,AC为边向△ABC外作正三角形ABD 和正三角形ACE,连结DC,BE,求证:DC=BE.
【拓展】如图 2所示,在四边形 ABCD 中,AB=BC=5,∠ABC=45°,连结 AC,BD,若∠DAC=90°,AC=AD,求 BD的长.
15.问题背景:
在△ABC中,已知AB,BC,AC三边的长分别为 ,求这个三角形的面积.
小辉在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不用求△ABC的高线长,借用网格就能计算出它的面积.我们把上述求△ABC 面积的方法叫做构图法.
(1)若△ABC三边的长分别为 请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
思维拓展:
(2)若△ABC三边的长分别为 且 m≠n),试运用构图法求出这个三角形的面积.
探索创新:
(3)已知a,b都是正数,a+b=3,求当a,b为何值时, 有最小值,并求出这个最小值.
16.【广西】《九章算术》是古代东方数学代表作,书中记载:今有开门去阔(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1,2所示(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点 D 距离门槛AB 都为1尺(1尺=10寸),则 AB的长是( ).
A.50.5寸 B.52寸 C.101寸 D.104寸
17.如图所示,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
18.如图所示,在△ABC中,∠BAC=90°,AB
1. A 2. B 3.11 4.42 或32 5.50
7.∵DE是AB边上的高,∴∠AED=∠BED=90°.在 Rt △ADE 中, 由 勾 股 定 理, 得 AE =
同理,在 Rt△BDE中,由勾股定理,得 BE=8,∴AB=2+8=10.
在△ABC中,由AB=10,AC=6,BC=8,得AB =AC +BC ,∴△ABC是直角三角形.
设△ABC的AB 边上的高为h,
则 即10h=6×8,∴h=4.8.
8.(1)∵∠F=90°,∠E=45°,∴∠EDF=45°.
∵∠ACB=90°,∠A=60°,∴∠ABC=30°.
∵AB∥CF,∴∠ABD=∠EDF=45°.
∴∠CBD=∠ABD-∠ABC=15°.
(2)如答图所示,过点 B 作 BM⊥FD于点 M.
∵∠ACB=90°,∠A=60°,AC=10,
∴∠ABC=30°.∴AB=20.
∵AB∥CF,∴∠BCM=30°.
由(1)知∠EDF=45°.∴MD=BM=5
∴CD=CM-MD=15-5
9. C 10. D11. C 12.2.9
14.【探究】∵以AB,AC为边分别向外作正三角形ABD 和正三角形ACE,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°.
∴∠DAB+∠BAC=∠EAC+∠BAC.
∴∠DAC=∠BAE.
在△DAC和△BAE中, ∴△DAC≌△BAE(SAS).∴DC=BE.
【拓展】如答图所示,以 AB 为边向 外 作 等 腰 直 角 三 角 形ABE,AE=AB,∠BAE=90°,∴∠BAD=∠EAC.
在△AEC和△ABD中,
∴△AEC≌△ABD.∴CE=BD.
15.(1)图略.
(3)如答图所示,构造AB=2,DE=5,BD=3,AB⊥BD,DE⊥BD,当A,C,E三点在同一条直线上时,AC+CE最小.过点A作AF∥BD,交 ED的延长线于点 F.
∴EF=AB+DE=7,AF=BD=3.
∴AC+CE的最小值是
的最小值是
16. C
17.设 BD=x,则CD=14-x.
在 Rt△ABD中,
在 Rt△ACD 中, 解得x=9.
∴AD=12.
证明:延长QM至点D,使MD=MQ,连结 PD,BD,BQ,CD.
在△CMQ和△BMD中,∵
∴△CMQ≌△BMD.
∴CQ=BD,∠QCM=∠DBM.
∴CQ∥BD.又∵∠BAC=90°.∴∠PBD=90°.
∵PM垂直平分DQ,∴PQ=PD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
