专题复习一 等腰三角形中的分类讨论与方程思想 同步练习(含答案)
文档属性
| 名称 | 专题复习一 等腰三角形中的分类讨论与方程思想 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 320.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 12:08:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习一 等腰三角形中的分类讨论与方程思想
1.若x,y满足 ,则以x,y的值为两边长的等腰三角形的周长为( ).
A.12 B.14 C.15 D.12 或15
2.若等腰三角形的周长是29,其中一边是7,则等腰三角形的底边长是( ).
A.15 B.7 C.15 或7 D.11
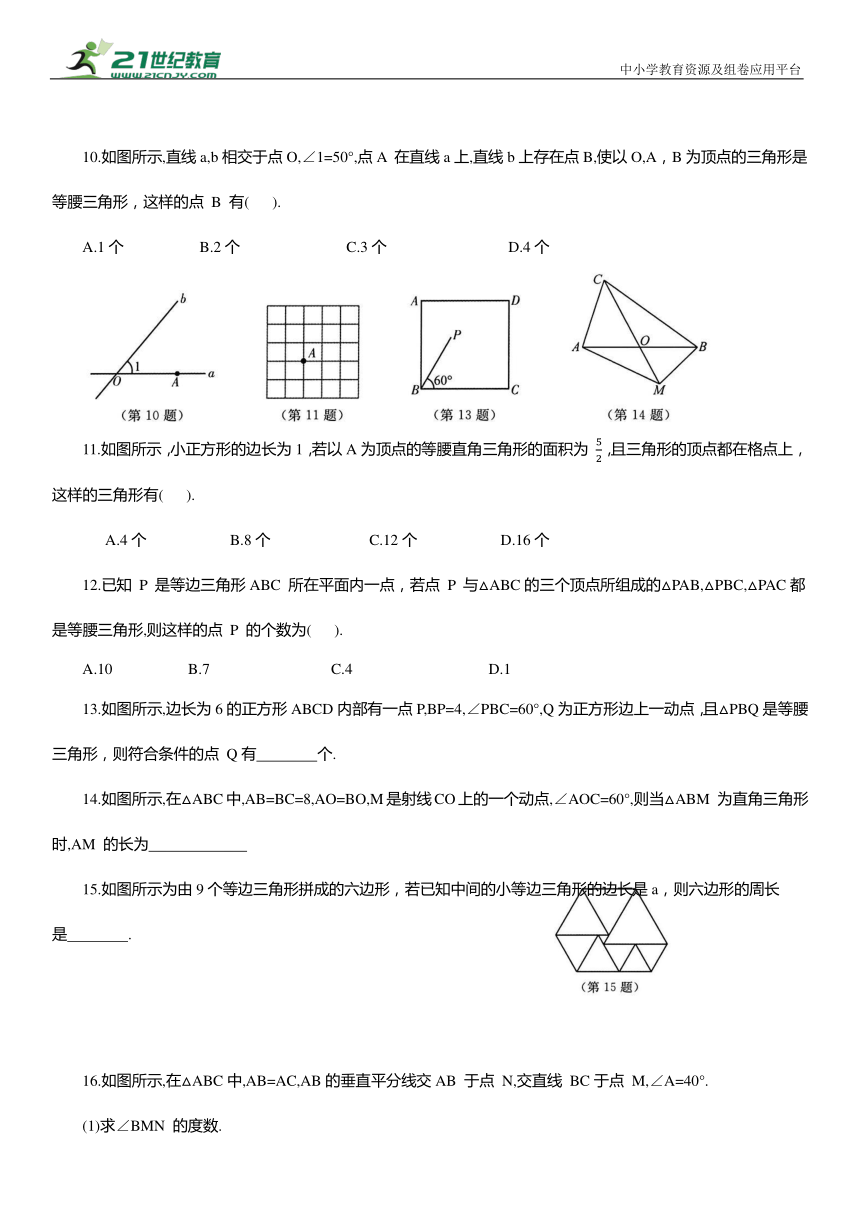
3.如图所示,在小长方形组成的网格中,每个小长方形的长为2,宽为1,A,B两点在网格的格点上,若点C也在网格的格点上,且△ABC是等腰三角形,则满足条件的点C的个数是( ).
A.2 B.3 C.4 D.5
4.如图所示,在△ABC中,AB=AC,AE=BE,∠BAE=40°,且AE=AF,则∠FEC等于( ).
A.10° B.15° C.20° D.25°
5.在等腰三角形ABC中,∠A 的相邻外角是70°,则∠B为 .
6.如图所示,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B为 .
7.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰三角形 ABC中,∠A=80°,则它的特征值k= .
8.如图所示,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个 用直尺与圆规画出相应的等腰三角形.
9.如图所示,在△ABC中,已知AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
10.如图所示,直线a,b相交于点O,∠1=50°,点A 在直线a上,直线b上存在点B,使以O,A,B为顶点的三角形是等腰三角形,这样的点 B 有( ).
A.1个 B.2个 C.3个 D.4个
11.如图所示,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为 ,且三角形的顶点都在格点上,这样的三角形有( ).
A.4个 B.8个 C.12个 D.16个
12.已知 P 是等边三角形ABC 所在平面内一点,若点 P 与△ABC的三个顶点所组成的△PAB,△PBC,△PAC都是等腰三角形,则这样的点 P 的个数为( ).
A.10 B.7 C.4 D.1
13.如图所示,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的点 Q有 个.
14.如图所示,在△ABC中,AB=BC=8,AO=BO,M是射线CO上的一个动点,∠AOC=60°,则当△ABM 为直角三角形时,AM 的长为
15.如图所示为由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是a,则六边形的周长是 .
16.如图所示,在△ABC中,AB=AC,AB的垂直平分线交AB 于点 N,交直线 BC于点 M,∠A=40°.
(1)求∠BMN 的度数.
(2)若将∠A 的度数改为80°,其余条件不变,再求∠M 的大小.
(3)你发现了怎样的规律 试证明.
(4)将(1)中的∠A改为钝角,(3)中的规律仍成立吗 若不成立,应怎样修改
17.如图所示,△ABC的面积为84,BC=21,现将△ABC沿直线BC 向右平移a(0(1)求 BC 边上的高.
(2)AB=10.
①求线段 DF 的长.
②连结AE,当△ABE为等腰三角形时,求a的值.
18.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,且其中的一个是等腰三角形,这样的直线最多可画( ).
A.3条 B.4条 C.5条 D.6条
19.如图所示的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点 B 落在AC 的中点D 处,折痕为 EF,那么 BF的长为 cm.
20.(1)已知在△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知在△ABC中,∠C是其最小的内角,过顶点 B 的一条直线把这个三角形分割成了两个等腰三角形,请探究∠ABC 与∠C之间的关系.
专题复习一 等腰三角形中的分类讨论与方程思想
1. C 2. B 3. C 4. C 5.35° 6.36° 7. 或 8.如答图所示.
△A OD,△A OD,△A OD,△A OD 就是所求的三角形.
9.设∠EBD=α.∵AD=DE=BE,BD=BC,AC=AB,∴∠A=∠AED,∠EBD=∠EDB=α,∠C=∠BDC,∠ABC=∠C=3α.
∵∠AED=∠EBD+∠EDB=2∠EBD,∴∠A=2α.
∵∠BDC=∠A+∠EBD=3α,∴∠ABC=∠C=3α.
∵∠A+∠C+∠ABC=180°,∴2α+3α+3α=180°.∴α=22.5°.∴∠A=2α=45°.
10. D 11. D 12. A 13.5 14.4 或 或4 15.30a
(2)同理得∠M=40°.
(3)规律是:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半.
证明:设∠A=α,则
(4)成立.
17.(1)如答图所示,作 AM⊥BC 于点 M.
∵△ABC的面积为84, 解得AM=8,即 BC边上的高为8.
(2)①在 Rt△ABM中, ∴CM=BC-BM=15.
在 Rt△ACM中, 由平移的性质可知,DF=AC=17.
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,则a=BE=12;
当EA=EB=a时,ME=a--6,
在 Rt△AME中,
即 解得
综上所述,当△ABE为等腰三角形时,a的值为10或12或
18. B
19. 【解析】如答图所示,过点 D 作 DH⊥BC于点H,过点 A作AN⊥BC于点 N.
∵AB=AC,∴∠B=∠C=30°.
根据折叠可得 DF=BF,∠EDF=∠B=30°.
∵AB=AC,BC=12cm,∴BN=NC=6cm.
∵点 B 落在AC 的中点 D 处,AN∥DH,
∴NH=HC=3cm.∴DH= cm.
设BF=DF=x(cm),则 FH=12-x--3=(9-x) cm.
在 Rt△DFH 中,
即
解得 即 BF的长为 cm.故答案为:
20.(1)如答图所示(共有2种不同的分割法).
(2)设∠C=x,∠ABC=y,过点 B的直线交边AC于点 D.
在△DBC中,
①若∠C是顶角,如答图3 所示,则 而∠ADB>90°,此时只能有∠A=∠ABD,即 180°- =540°,即
②若∠C是底角,有两种情况:
第一种情况,如答图4所示,当DB=DC时,则∠DBC=x,∠ADB=2x,∠ABD=y-x.
由AB=AD,得2x=y-x,此时y=3x,即∠ABC=3∠C.
由AB=BD,得
此时3x+y=180°,即.
由AD=BD,得
此时y=90°,即∠ABC=90°,∠C为小于 45°的任意锐角.
第二种情况,如答图5所示,当 BD=BC时,∠BDC= 此时只能有 AD=BD.故 与∠C 是最小角矛盾.∴当∠C是底角时,BD=BC不成立.
综上所述,∠ABC与∠C之间的关系是:∠ABC= 或∠ABC=3∠C 或∠ABC=180°-3∠C或∠ABC=90°,∠C为小于 45°的任意角.
专题复习一 等腰三角形中的分类讨论与方程思想
1.若x,y满足 ,则以x,y的值为两边长的等腰三角形的周长为( ).
A.12 B.14 C.15 D.12 或15
2.若等腰三角形的周长是29,其中一边是7,则等腰三角形的底边长是( ).
A.15 B.7 C.15 或7 D.11
3.如图所示,在小长方形组成的网格中,每个小长方形的长为2,宽为1,A,B两点在网格的格点上,若点C也在网格的格点上,且△ABC是等腰三角形,则满足条件的点C的个数是( ).
A.2 B.3 C.4 D.5
4.如图所示,在△ABC中,AB=AC,AE=BE,∠BAE=40°,且AE=AF,则∠FEC等于( ).
A.10° B.15° C.20° D.25°
5.在等腰三角形ABC中,∠A 的相邻外角是70°,则∠B为 .
6.如图所示,BC=BD,AD=AE,DE=CE,∠A=36°,则∠B为 .
7.定义:等腰三角形的顶角与其一个底角的度数的比值k称为这个等腰三角形的“特征值”.若等腰三角形 ABC中,∠A=80°,则它的特征值k= .
8.如图所示,线段OD的一个端点O在直线a上,以OD为一边画等腰三角形,并且使另一个顶点在直线a上,这样的等腰三角形能画多少个 用直尺与圆规画出相应的等腰三角形.
9.如图所示,在△ABC中,已知AB=AC,BC=BD,AD=DE=EB,求∠A的度数.
10.如图所示,直线a,b相交于点O,∠1=50°,点A 在直线a上,直线b上存在点B,使以O,A,B为顶点的三角形是等腰三角形,这样的点 B 有( ).
A.1个 B.2个 C.3个 D.4个
11.如图所示,小正方形的边长为1,若以A为顶点的等腰直角三角形的面积为 ,且三角形的顶点都在格点上,这样的三角形有( ).
A.4个 B.8个 C.12个 D.16个
12.已知 P 是等边三角形ABC 所在平面内一点,若点 P 与△ABC的三个顶点所组成的△PAB,△PBC,△PAC都是等腰三角形,则这样的点 P 的个数为( ).
A.10 B.7 C.4 D.1
13.如图所示,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的点 Q有 个.
14.如图所示,在△ABC中,AB=BC=8,AO=BO,M是射线CO上的一个动点,∠AOC=60°,则当△ABM 为直角三角形时,AM 的长为
15.如图所示为由9个等边三角形拼成的六边形,若已知中间的小等边三角形的边长是a,则六边形的周长是 .
16.如图所示,在△ABC中,AB=AC,AB的垂直平分线交AB 于点 N,交直线 BC于点 M,∠A=40°.
(1)求∠BMN 的度数.
(2)若将∠A 的度数改为80°,其余条件不变,再求∠M 的大小.
(3)你发现了怎样的规律 试证明.
(4)将(1)中的∠A改为钝角,(3)中的规律仍成立吗 若不成立,应怎样修改
17.如图所示,△ABC的面积为84,BC=21,现将△ABC沿直线BC 向右平移a(0
(2)AB=10.
①求线段 DF 的长.
②连结AE,当△ABE为等腰三角形时,求a的值.
18.已知△ABC的三边长分别为4,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,且其中的一个是等腰三角形,这样的直线最多可画( ).
A.3条 B.4条 C.5条 D.6条
19.如图所示的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点 B 落在AC 的中点D 处,折痕为 EF,那么 BF的长为 cm.
20.(1)已知在△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
(2)已知在△ABC中,∠C是其最小的内角,过顶点 B 的一条直线把这个三角形分割成了两个等腰三角形,请探究∠ABC 与∠C之间的关系.
专题复习一 等腰三角形中的分类讨论与方程思想
1. C 2. B 3. C 4. C 5.35° 6.36° 7. 或 8.如答图所示.
△A OD,△A OD,△A OD,△A OD 就是所求的三角形.
9.设∠EBD=α.∵AD=DE=BE,BD=BC,AC=AB,∴∠A=∠AED,∠EBD=∠EDB=α,∠C=∠BDC,∠ABC=∠C=3α.
∵∠AED=∠EBD+∠EDB=2∠EBD,∴∠A=2α.
∵∠BDC=∠A+∠EBD=3α,∴∠ABC=∠C=3α.
∵∠A+∠C+∠ABC=180°,∴2α+3α+3α=180°.∴α=22.5°.∴∠A=2α=45°.
10. D 11. D 12. A 13.5 14.4 或 或4 15.30a
(2)同理得∠M=40°.
(3)规律是:等腰三角形一腰的垂直平分线与底边所在直线相交所成的锐角等于顶角的一半.
证明:设∠A=α,则
(4)成立.
17.(1)如答图所示,作 AM⊥BC 于点 M.
∵△ABC的面积为84, 解得AM=8,即 BC边上的高为8.
(2)①在 Rt△ABM中, ∴CM=BC-BM=15.
在 Rt△ACM中, 由平移的性质可知,DF=AC=17.
②当AB=BE=10时,a=BE=10;
当AB=AE=10时,BE=2BM=12,则a=BE=12;
当EA=EB=a时,ME=a--6,
在 Rt△AME中,
即 解得
综上所述,当△ABE为等腰三角形时,a的值为10或12或
18. B
19. 【解析】如答图所示,过点 D 作 DH⊥BC于点H,过点 A作AN⊥BC于点 N.
∵AB=AC,∴∠B=∠C=30°.
根据折叠可得 DF=BF,∠EDF=∠B=30°.
∵AB=AC,BC=12cm,∴BN=NC=6cm.
∵点 B 落在AC 的中点 D 处,AN∥DH,
∴NH=HC=3cm.∴DH= cm.
设BF=DF=x(cm),则 FH=12-x--3=(9-x) cm.
在 Rt△DFH 中,
即
解得 即 BF的长为 cm.故答案为:
20.(1)如答图所示(共有2种不同的分割法).
(2)设∠C=x,∠ABC=y,过点 B的直线交边AC于点 D.
在△DBC中,
①若∠C是顶角,如答图3 所示,则 而∠ADB>90°,此时只能有∠A=∠ABD,即 180°- =540°,即
②若∠C是底角,有两种情况:
第一种情况,如答图4所示,当DB=DC时,则∠DBC=x,∠ADB=2x,∠ABD=y-x.
由AB=AD,得2x=y-x,此时y=3x,即∠ABC=3∠C.
由AB=BD,得
此时3x+y=180°,即.
由AD=BD,得
此时y=90°,即∠ABC=90°,∠C为小于 45°的任意锐角.
第二种情况,如答图5所示,当 BD=BC时,∠BDC= 此时只能有 AD=BD.故 与∠C 是最小角矛盾.∴当∠C是底角时,BD=BC不成立.
综上所述,∠ABC与∠C之间的关系是:∠ABC= 或∠ABC=3∠C 或∠ABC=180°-3∠C或∠ABC=90°,∠C为小于 45°的任意角.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
