2.8 直角三角形全等的判定同步练习 (含答案)-2024-2025学年浙教版八年级数学上册
文档属性
| 名称 | 2.8 直角三角形全等的判定同步练习 (含答案)-2024-2025学年浙教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 307.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-25 15:32:54 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.8 直角三角形全等的判定
1.下列各选项中的两个直角三角形不一定全等的是( ).
A.两条直角边对应相等的两个直角三角形
B.两个锐角对应相等的两个直角三角形
C.斜边和一条直角边对应相等的两个直角三角形
D.有一个锐角及这个锐角的对边对应相等的两个直角三角形
2.如图所示,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是( ).
A. HL B. ASA C. SAS D. AAS
3.如图所示,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE交CE 的延长线于点D,AE=5cm,BD=2cm,则 DE的长是( ).
A.8cm B.5cm C.3cm D.2cm
4.如图所示,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE 交于点F,若BF=AC,则∠ABC的大小是( ).
A.40° B.45° C.50° D.60°
5.如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点 B,C作过点A 的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
6.如图所示,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段 PQ=AB,P,Q两点分别在AC和过点A且垂直于 AC的射线 AO上运动,当AP= 时,△ABC和△PQA全等.
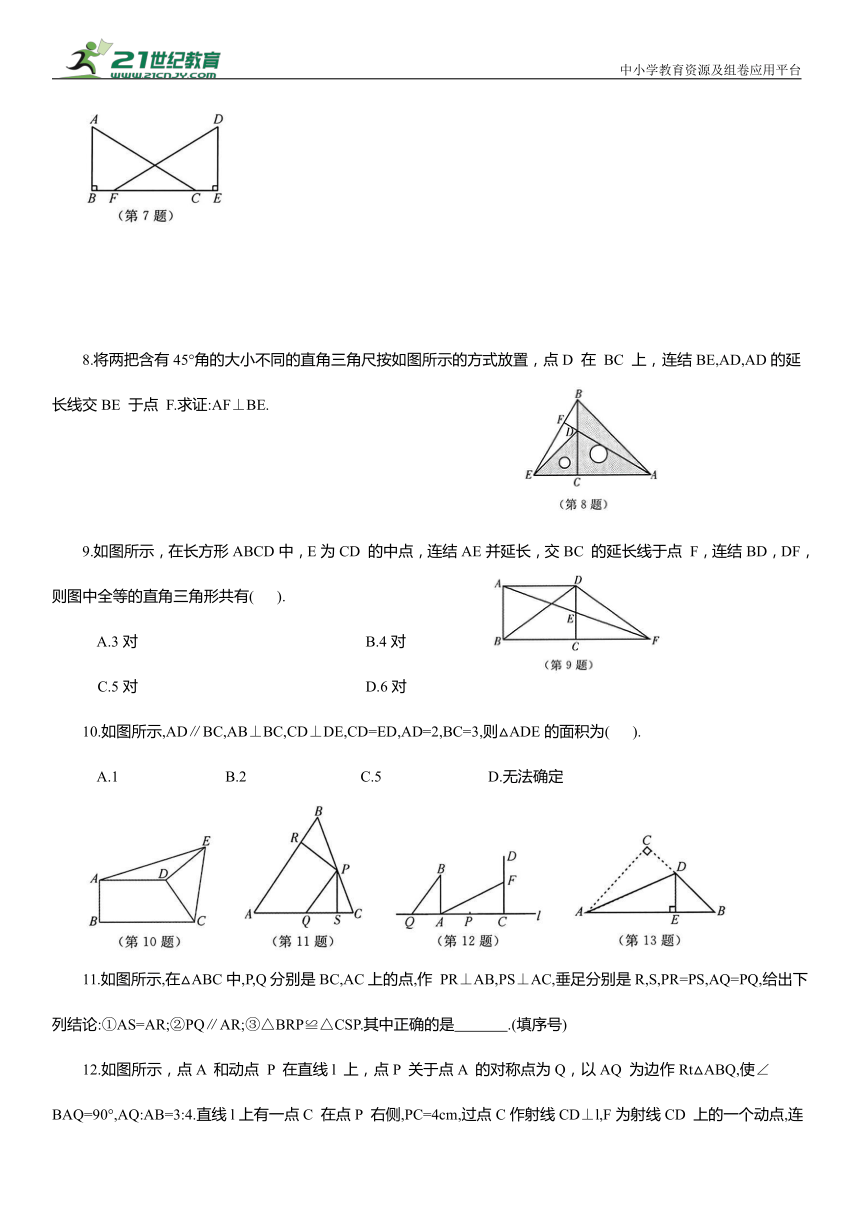
7.如图所示,点B,F,C,E在同一条直线上,AB⊥BE,DE⊥BE,连结AC,DF,且AC=DF,BF=CE,求证:AB=DE.
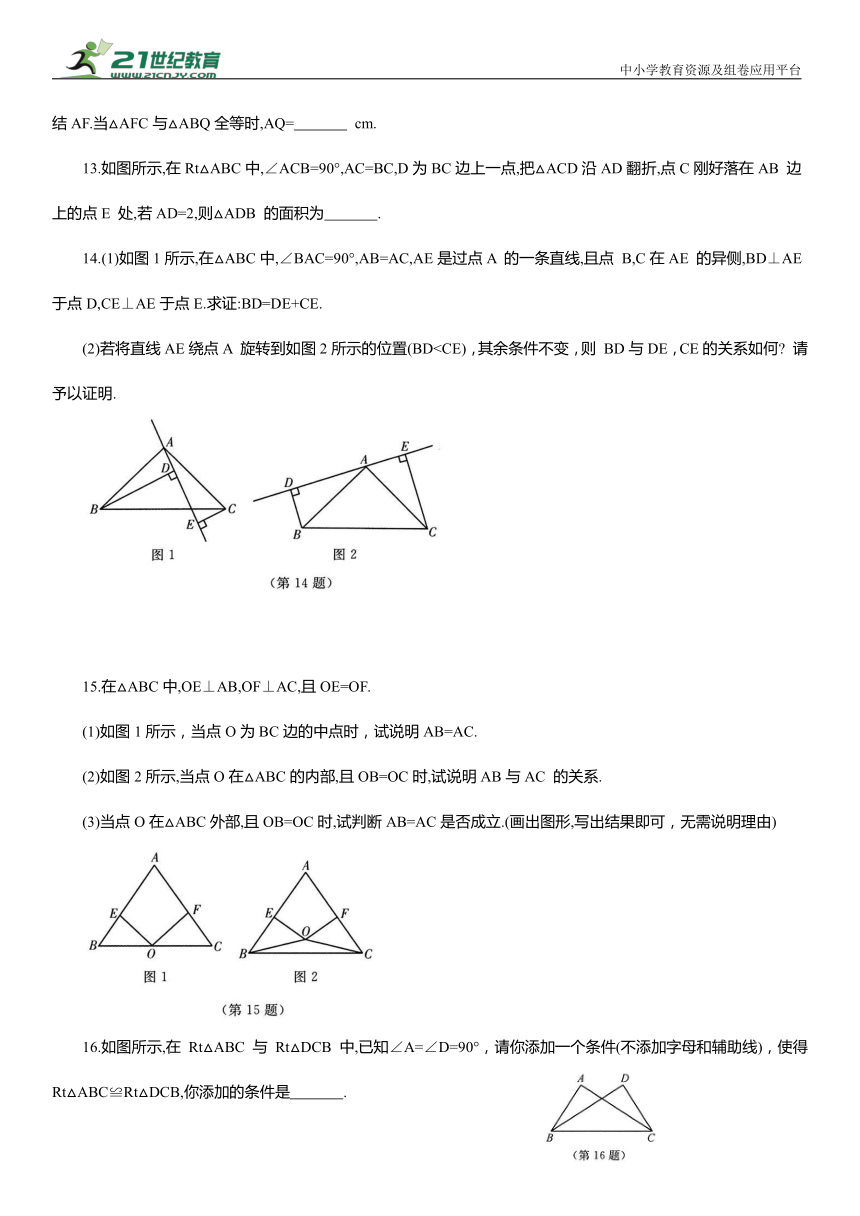
8.将两把含有45°角的大小不同的直角三角尺按如图所示的方式放置,点D 在 BC 上,连结BE,AD,AD的延长线交BE 于点 F.求证:AF⊥BE.
9.如图所示,在长方形ABCD中,E为CD 的中点,连结AE并延长,交BC 的延长线于点 F,连结BD,DF,则图中全等的直角三角形共有( ).
A.3对 B.4对
C.5对 D.6对
10.如图所示,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( ).
A.1 B.2 C.5 D.无法确定
11.如图所示,在△ABC中,P,Q分别是BC,AC上的点,作 PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,给出下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是 .(填序号)
12.如图所示,点A 和动点 P 在直线l 上,点P 关于点A 的对称点为Q,以AQ 为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4.直线l上有一点C 在点P 右侧,PC=4cm,过点C作射线CD⊥l,F为射线CD 上的一个动点,连结AF.当△AFC与△ABQ全等时,AQ= cm.
13.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上一点,把△ACD沿AD翻折,点C刚好落在AB 边上的点E 处,若AD=2,则△ADB 的面积为 .
14.(1)如图1所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A 的一条直线,且点 B,C在AE 的异侧,BD⊥AE于点D,CE⊥AE于点E.求证:BD=DE+CE.
(2)若将直线AE绕点A 旋转到如图2所示的位置(BD15.在△ABC中,OE⊥AB,OF⊥AC,且OE=OF.
(1)如图1所示,当点O为BC边的中点时,试说明AB=AC.
(2)如图2所示,当点O在△ABC的内部,且OB=OC时,试说明AB与AC 的关系.
(3)当点O在△ABC外部,且OB=OC时,试判断AB=AC是否成立.(画出图形,写出结果即可,无需说明理由)
16.如图所示,在 Rt△ABC 与 Rt△DCB 中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使得 Rt△ABC≌Rt△DCB,你添加的条件是 .
17.如图所示,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB∥CD.
18.如图所示,在等腰直角三角形 DBC中,∠BDC=90°,BF平分∠DBC,与CD 相交于点F,延长 BD到点A,使DA=DF.
(1)试说明:△FBD≌△ACD.
(2)延长 BF交AC 于点 E,试说明:
(3)在(2)的条件下,若H是BC 边的中点,连结DH与BE 相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
2.8 直角三角形全等的判定
1. B 2. A 3. C 4. B 5.7 6.5 或10
7.∵BF=CE,∴BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.在 Rt△ABC 和 Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).∴AB=DE.
8. 由 题 意 得∠DEC=∠EDC= 45°,∠CBA =∠CAB=45°,∴EC=DC,BC=AC.
在△BEC和△ADC中,.
∴△BEC≌△ADC.∴∠EBC=∠DAC.
∵∠DAC+∠CDA=90°,∠FDB=∠CDA,
∴∠EBC+∠FDB=90°.∴∠BFD=90°,即 AF⊥BE.
9. B 10. A 11.①② 12.12 或 13.1
14.(1)∵BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°.∴∠ABD+∠BAE=90°.
∵∠CAE+∠BAE=90°,∴∠ABD=∠CAE.
在△ABD 和△CAE中,
∴△ABD≌△CAE.∴BD=AE,AD=CE.
∴BD=AE=AD+DE=DE+CE.
(2)BD=DE-CE.
证明:同(1)可证得△ABD≌△CAE,
∴BD=AE,AD=CE.∴AE+AD=BD+CE.
∴DE=BD+CE.∴BD=DE--CE.
15.(1)在 Rt△OBE 和 Rt△OCF中, ∴Rt△OBE≌Rt△OCF(HL).∴∠B=∠C.
∴AB=AC.
(2)同(1)可证得 Rt△OBE≌Rt△OCF,∴∠OBE=∠OCF.∵OB=OC,∴∠OBC=∠OCB.∴∠ABC=∠ACB.∴AB=AC.
(3)①当 BC 的垂直平分线与∠BAC 的平分线重合时,AB=AC成立.
②当 BC的垂直平分线与∠BAC的平分线不重合时,结论不成立.(图形不唯一,符合题意,画图规范即可)
16. AB=DC(答案不唯一)
17.∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF.∴BE=DF.
在 Rt△AEB 和 Rt△CFD中,∵(AB=CDF,
∴Rt△AEB≌Rt△CFD(HL).∴∠B=∠D.
∴AB∥CD.
18.(1)略
(2)∵△FBD≌△ACD,
∴BF=AC,∠FBD=∠ACD.
∴∠ECF+∠EFC=∠FBD+∠DFB=90°.
∴∠FEC=90°.
又∵BF平分∠DBC,∴∠ABE=∠CBE.
在△ABE 和△CBE中,
∴△ABE≌△CBE.∴CE=AE= AC= BF.
理由如下:连结 CG.
∵BD=CD,H 是BC 边的中点,
∴DH 是 BC 的中垂线.∴BG=CG.
在 Rt△CGE中,( BG .
2.8 直角三角形全等的判定
1.下列各选项中的两个直角三角形不一定全等的是( ).
A.两条直角边对应相等的两个直角三角形
B.两个锐角对应相等的两个直角三角形
C.斜边和一条直角边对应相等的两个直角三角形
D.有一个锐角及这个锐角的对边对应相等的两个直角三角形
2.如图所示,∠BAD=∠BCD=90°,AB=CB,可以证明△BAD≌△BCD的理由是( ).
A. HL B. ASA C. SAS D. AAS
3.如图所示,∠ACB=90°,AC=BC,AE⊥CE于点E,BD⊥CE交CE 的延长线于点D,AE=5cm,BD=2cm,则 DE的长是( ).
A.8cm B.5cm C.3cm D.2cm
4.如图所示,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE 交于点F,若BF=AC,则∠ABC的大小是( ).
A.40° B.45° C.50° D.60°
5.如图所示,在Rt△ABC中,∠BAC=90°,AB=AC,分别过点 B,C作过点A 的直线的垂线BD,CE,若BD=4cm,CE=3cm,则DE= cm.
6.如图所示,在Rt△ABC中,∠C=90°,AC=10,BC=5,线段 PQ=AB,P,Q两点分别在AC和过点A且垂直于 AC的射线 AO上运动,当AP= 时,△ABC和△PQA全等.
7.如图所示,点B,F,C,E在同一条直线上,AB⊥BE,DE⊥BE,连结AC,DF,且AC=DF,BF=CE,求证:AB=DE.
8.将两把含有45°角的大小不同的直角三角尺按如图所示的方式放置,点D 在 BC 上,连结BE,AD,AD的延长线交BE 于点 F.求证:AF⊥BE.
9.如图所示,在长方形ABCD中,E为CD 的中点,连结AE并延长,交BC 的延长线于点 F,连结BD,DF,则图中全等的直角三角形共有( ).
A.3对 B.4对
C.5对 D.6对
10.如图所示,AD∥BC,AB⊥BC,CD⊥DE,CD=ED,AD=2,BC=3,则△ADE的面积为( ).
A.1 B.2 C.5 D.无法确定
11.如图所示,在△ABC中,P,Q分别是BC,AC上的点,作 PR⊥AB,PS⊥AC,垂足分别是R,S,PR=PS,AQ=PQ,给出下列结论:①AS=AR;②PQ∥AR;③△BRP≌△CSP.其中正确的是 .(填序号)
12.如图所示,点A 和动点 P 在直线l 上,点P 关于点A 的对称点为Q,以AQ 为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4.直线l上有一点C 在点P 右侧,PC=4cm,过点C作射线CD⊥l,F为射线CD 上的一个动点,连结AF.当△AFC与△ABQ全等时,AQ= cm.
13.如图所示,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC边上一点,把△ACD沿AD翻折,点C刚好落在AB 边上的点E 处,若AD=2,则△ADB 的面积为 .
14.(1)如图1所示,在△ABC中,∠BAC=90°,AB=AC,AE是过点A 的一条直线,且点 B,C在AE 的异侧,BD⊥AE于点D,CE⊥AE于点E.求证:BD=DE+CE.
(2)若将直线AE绕点A 旋转到如图2所示的位置(BD
(1)如图1所示,当点O为BC边的中点时,试说明AB=AC.
(2)如图2所示,当点O在△ABC的内部,且OB=OC时,试说明AB与AC 的关系.
(3)当点O在△ABC外部,且OB=OC时,试判断AB=AC是否成立.(画出图形,写出结果即可,无需说明理由)
16.如图所示,在 Rt△ABC 与 Rt△DCB 中,已知∠A=∠D=90°,请你添加一个条件(不添加字母和辅助线),使得 Rt△ABC≌Rt△DCB,你添加的条件是 .
17.如图所示,已知AB=CD,AE⊥BD,CF⊥BD,垂足分别为E,F,BF=DE.求证:AB∥CD.
18.如图所示,在等腰直角三角形 DBC中,∠BDC=90°,BF平分∠DBC,与CD 相交于点F,延长 BD到点A,使DA=DF.
(1)试说明:△FBD≌△ACD.
(2)延长 BF交AC 于点 E,试说明:
(3)在(2)的条件下,若H是BC 边的中点,连结DH与BE 相交于点G.试探索CE,GE,BG之间的数量关系,并说明理由.
2.8 直角三角形全等的判定
1. B 2. A 3. C 4. B 5.7 6.5 或10
7.∵BF=CE,∴BC=EF.
∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°.在 Rt△ABC 和 Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).∴AB=DE.
8. 由 题 意 得∠DEC=∠EDC= 45°,∠CBA =∠CAB=45°,∴EC=DC,BC=AC.
在△BEC和△ADC中,.
∴△BEC≌△ADC.∴∠EBC=∠DAC.
∵∠DAC+∠CDA=90°,∠FDB=∠CDA,
∴∠EBC+∠FDB=90°.∴∠BFD=90°,即 AF⊥BE.
9. B 10. A 11.①② 12.12 或 13.1
14.(1)∵BD⊥AE,CE⊥AE,∴∠BDA=∠AEC=90°.∴∠ABD+∠BAE=90°.
∵∠CAE+∠BAE=90°,∴∠ABD=∠CAE.
在△ABD 和△CAE中,
∴△ABD≌△CAE.∴BD=AE,AD=CE.
∴BD=AE=AD+DE=DE+CE.
(2)BD=DE-CE.
证明:同(1)可证得△ABD≌△CAE,
∴BD=AE,AD=CE.∴AE+AD=BD+CE.
∴DE=BD+CE.∴BD=DE--CE.
15.(1)在 Rt△OBE 和 Rt△OCF中, ∴Rt△OBE≌Rt△OCF(HL).∴∠B=∠C.
∴AB=AC.
(2)同(1)可证得 Rt△OBE≌Rt△OCF,∴∠OBE=∠OCF.∵OB=OC,∴∠OBC=∠OCB.∴∠ABC=∠ACB.∴AB=AC.
(3)①当 BC 的垂直平分线与∠BAC 的平分线重合时,AB=AC成立.
②当 BC的垂直平分线与∠BAC的平分线不重合时,结论不成立.(图形不唯一,符合题意,画图规范即可)
16. AB=DC(答案不唯一)
17.∵AE⊥BD,CF⊥BD,∴∠AEB=∠CFD=90°.
∵BF=DE,∴BF+EF=DE+EF.∴BE=DF.
在 Rt△AEB 和 Rt△CFD中,∵(AB=CDF,
∴Rt△AEB≌Rt△CFD(HL).∴∠B=∠D.
∴AB∥CD.
18.(1)略
(2)∵△FBD≌△ACD,
∴BF=AC,∠FBD=∠ACD.
∴∠ECF+∠EFC=∠FBD+∠DFB=90°.
∴∠FEC=90°.
又∵BF平分∠DBC,∴∠ABE=∠CBE.
在△ABE 和△CBE中,
∴△ABE≌△CBE.∴CE=AE= AC= BF.
理由如下:连结 CG.
∵BD=CD,H 是BC 边的中点,
∴DH 是 BC 的中垂线.∴BG=CG.
在 Rt△CGE中,( BG .
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
