2.7 探索勾股定理(2)同步练习(含答案)
文档属性
| 名称 | 2.7 探索勾股定理(2)同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 230.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.7 探索勾股定理(2)
1.在Rt△ABC中,若 则下列结论中,正确的是( ).
A.∠B=90° B.∠C=90°
C.△ABC是锐角三角形 D.△ABC是钝角三角形
2.已知△ABC的三边长分别是6cm,8cm,10cm,则△ABC的面积是( ).
C.40cm D.48cm
3.已知△ABC中,a,b,c分别是∠A,∠B,∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( ).
A.∠A=∠C-∠B B. a:b:c=2:3:4
4.如图所示,将长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至点D,则橡皮筋被拉长了( ).
A.2cm B.3cm C.4cm D.5cm
5.现有两根铁棒,它们的长分别为15cm和20cm,若想焊接一个直角三角形的铁架,则第三根铁棒的长度为 .
6.如图所示为一块农家菜地的平面图,其中AD=4cm,CD=3cm,AB=13cm,BC=12cm,∠ADC=90°,则这块菜地的面积为 cm .
7.如图所示,在5×5的方格纸中,每一个小正方形的边长都为1.四边形ABCD的顶点都在格点上.
(1)∠BCD 是不是直角 请说明理由.
(2)求四边形 ABCD的面积.(可以根据需要添加字母)
8.已知三角形的三边分别为a,b,c,且
(1)请判断这个三角形的形状.
(2)试找出一组a,b,c,使三角形的最短边不小于20,另两边的差为2,三边均为正整数.
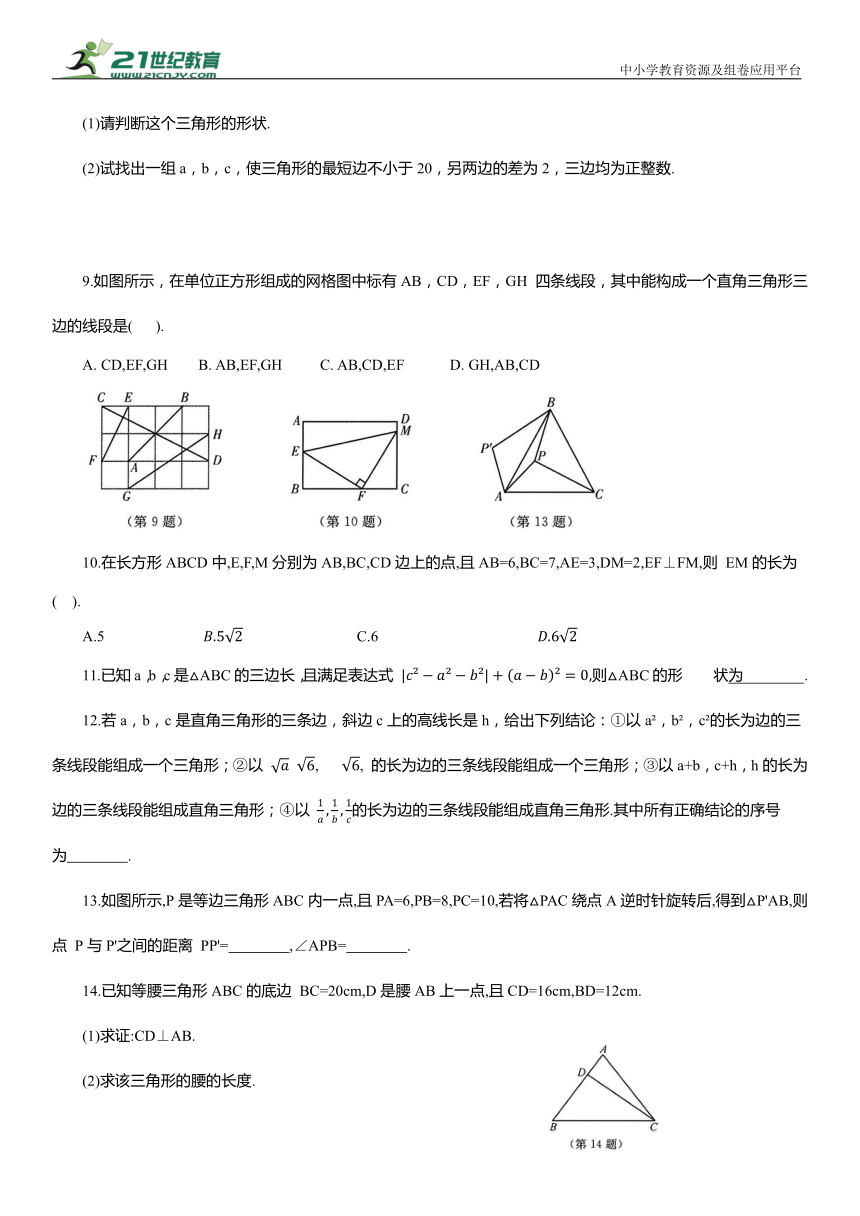
9.如图所示,在单位正方形组成的网格图中标有AB,CD,EF,GH 四条线段,其中能构成一个直角三角形三边的线段是( ).
A. CD,EF,GH B. AB,EF,GH C. AB,CD,EF D. GH,AB,CD
10.在长方形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则 EM的长为( ).
A.5 C.6
11.已知a,b,c是△ABC的三边长,且满足表达式 则△ABC的形 状为 .
12.若a,b,c是直角三角形的三条边,斜边c上的高线长是h,给出下列结论:①以a ,b ,c 的长为边的三条线段能组成一个三角形;②以 , , 的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以 的长为边的三条线段能组成直角三角形.其中所有正确结论的序号为 .
13.如图所示,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P'AB,则点 P与P'之间的距离 PP'= ,∠APB= .
14.已知等腰三角形ABC的底边 BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.
(1)求证:CD⊥AB.
(2)求该三角形的腰的长度.
15.如图所示,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,D为AC边上的动点,点D从点C出发沿边CA 往点A 运动,当运动到点A时停止,若设点D 运动的时间为t(s),点D运动的速度为每秒2个单位长度.
(1)当t=2s时,CD= ,AD= .
(2)当t= 时,△CBD是直角三角形.
(3)当t为何值时,△CBD是等腰三角形 请说明理由.
16.已知M,N是线段AB 上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连结AC,BC,则△ABC一定是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
17.如图所示,在△ABC中,AC=5,BC=12,AB=13,CD是AB边上的中线,则CD= .
18.王老师在一次探究性学习课程中,设计了如下数表:
n 2 3 4 5
a 2 -1 3 -1 4 —1 5 -1
b 4 6 8 10
c 2 +1 3 +1 4 +1 5 +1
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边的三角形是否为直角三角形 证明你的结论.
(3)观察下列勾股数 ,分析其中的规律,根据规律写出第五组勾股数.
2.7 探索勾股定理(2)
1. B 2. A 3. B 4. A 5.25cm或5 cm 6.247.(1)∠BCD是直角.理由如下:连结 BD.
4 =25,∴BD =BC +CD .∴∠BCD是直角.
即四边形 ABCD的面积是14.5.
∴这个三角形是直角三角形.
(2)取b=20,即
∴a=m--1=99,c=m+1=101.
9. B 10. B 11.等腰直角三角形 12.②③13.6 150°
14.(1)∵BC=20cm,CD=16cm,BD=12cm,∴满足
∴根据勾股定理的逆定理可知,∠BDC=90°,即CD⊥AB.
(2)设腰长为x(cm),则AD=x--12.
由(1)可知
即 解得
∴腰长为
15.(1)4 21 (2)4.5 或12.5s
(3)①当CD=BD时,如答图1 所示,过点 D 作DE⊥BC于点E,则
②当CD=BC时,CD=15,
③当 BD=BC时,如答图2 所示,过点 B 作 BF⊥AC于点F,则CF=9,CD=2CF=18,∴t=9.
综上所述 或 或9s时,△CBD是等腰三角形.
16. B17.6.5
(2)是直角三角形.证明:
∴以a,b,c为边的三角形是直角三角形.
2.7 探索勾股定理(2)
1.在Rt△ABC中,若 则下列结论中,正确的是( ).
A.∠B=90° B.∠C=90°
C.△ABC是锐角三角形 D.△ABC是钝角三角形
2.已知△ABC的三边长分别是6cm,8cm,10cm,则△ABC的面积是( ).
C.40cm D.48cm
3.已知△ABC中,a,b,c分别是∠A,∠B,∠C的对边,下列条件中,不能判断△ABC是直角三角形的是( ).
A.∠A=∠C-∠B B. a:b:c=2:3:4
4.如图所示,将长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm至点D,则橡皮筋被拉长了( ).
A.2cm B.3cm C.4cm D.5cm
5.现有两根铁棒,它们的长分别为15cm和20cm,若想焊接一个直角三角形的铁架,则第三根铁棒的长度为 .
6.如图所示为一块农家菜地的平面图,其中AD=4cm,CD=3cm,AB=13cm,BC=12cm,∠ADC=90°,则这块菜地的面积为 cm .
7.如图所示,在5×5的方格纸中,每一个小正方形的边长都为1.四边形ABCD的顶点都在格点上.
(1)∠BCD 是不是直角 请说明理由.
(2)求四边形 ABCD的面积.(可以根据需要添加字母)
8.已知三角形的三边分别为a,b,c,且
(1)请判断这个三角形的形状.
(2)试找出一组a,b,c,使三角形的最短边不小于20,另两边的差为2,三边均为正整数.
9.如图所示,在单位正方形组成的网格图中标有AB,CD,EF,GH 四条线段,其中能构成一个直角三角形三边的线段是( ).
A. CD,EF,GH B. AB,EF,GH C. AB,CD,EF D. GH,AB,CD
10.在长方形ABCD中,E,F,M分别为AB,BC,CD边上的点,且AB=6,BC=7,AE=3,DM=2,EF⊥FM,则 EM的长为( ).
A.5 C.6
11.已知a,b,c是△ABC的三边长,且满足表达式 则△ABC的形 状为 .
12.若a,b,c是直角三角形的三条边,斜边c上的高线长是h,给出下列结论:①以a ,b ,c 的长为边的三条线段能组成一个三角形;②以 , , 的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以 的长为边的三条线段能组成直角三角形.其中所有正确结论的序号为 .
13.如图所示,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P'AB,则点 P与P'之间的距离 PP'= ,∠APB= .
14.已知等腰三角形ABC的底边 BC=20cm,D是腰AB上一点,且CD=16cm,BD=12cm.
(1)求证:CD⊥AB.
(2)求该三角形的腰的长度.
15.如图所示,在Rt△ABC中,∠ABC=90°,AB=20,BC=15,D为AC边上的动点,点D从点C出发沿边CA 往点A 运动,当运动到点A时停止,若设点D 运动的时间为t(s),点D运动的速度为每秒2个单位长度.
(1)当t=2s时,CD= ,AD= .
(2)当t= 时,△CBD是直角三角形.
(3)当t为何值时,△CBD是等腰三角形 请说明理由.
16.已知M,N是线段AB 上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连结AC,BC,则△ABC一定是( ).
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
17.如图所示,在△ABC中,AC=5,BC=12,AB=13,CD是AB边上的中线,则CD= .
18.王老师在一次探究性学习课程中,设计了如下数表:
n 2 3 4 5
a 2 -1 3 -1 4 —1 5 -1
b 4 6 8 10
c 2 +1 3 +1 4 +1 5 +1
(1)请你分别观察a,b,c与n之间的关系,并用含自然数n(n>1)的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边的三角形是否为直角三角形 证明你的结论.
(3)观察下列勾股数 ,分析其中的规律,根据规律写出第五组勾股数.
2.7 探索勾股定理(2)
1. B 2. A 3. B 4. A 5.25cm或5 cm 6.247.(1)∠BCD是直角.理由如下:连结 BD.
4 =25,∴BD =BC +CD .∴∠BCD是直角.
即四边形 ABCD的面积是14.5.
∴这个三角形是直角三角形.
(2)取b=20,即
∴a=m--1=99,c=m+1=101.
9. B 10. B 11.等腰直角三角形 12.②③13.6 150°
14.(1)∵BC=20cm,CD=16cm,BD=12cm,∴满足
∴根据勾股定理的逆定理可知,∠BDC=90°,即CD⊥AB.
(2)设腰长为x(cm),则AD=x--12.
由(1)可知
即 解得
∴腰长为
15.(1)4 21 (2)4.5 或12.5s
(3)①当CD=BD时,如答图1 所示,过点 D 作DE⊥BC于点E,则
②当CD=BC时,CD=15,
③当 BD=BC时,如答图2 所示,过点 B 作 BF⊥AC于点F,则CF=9,CD=2CF=18,∴t=9.
综上所述 或 或9s时,△CBD是等腰三角形.
16. B17.6.5
(2)是直角三角形.证明:
∴以a,b,c为边的三角形是直角三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
