第2章 特殊三角形单元提优测试卷(含答案)
文档属性
| 名称 | 第2章 特殊三角形单元提优测试卷(含答案) | 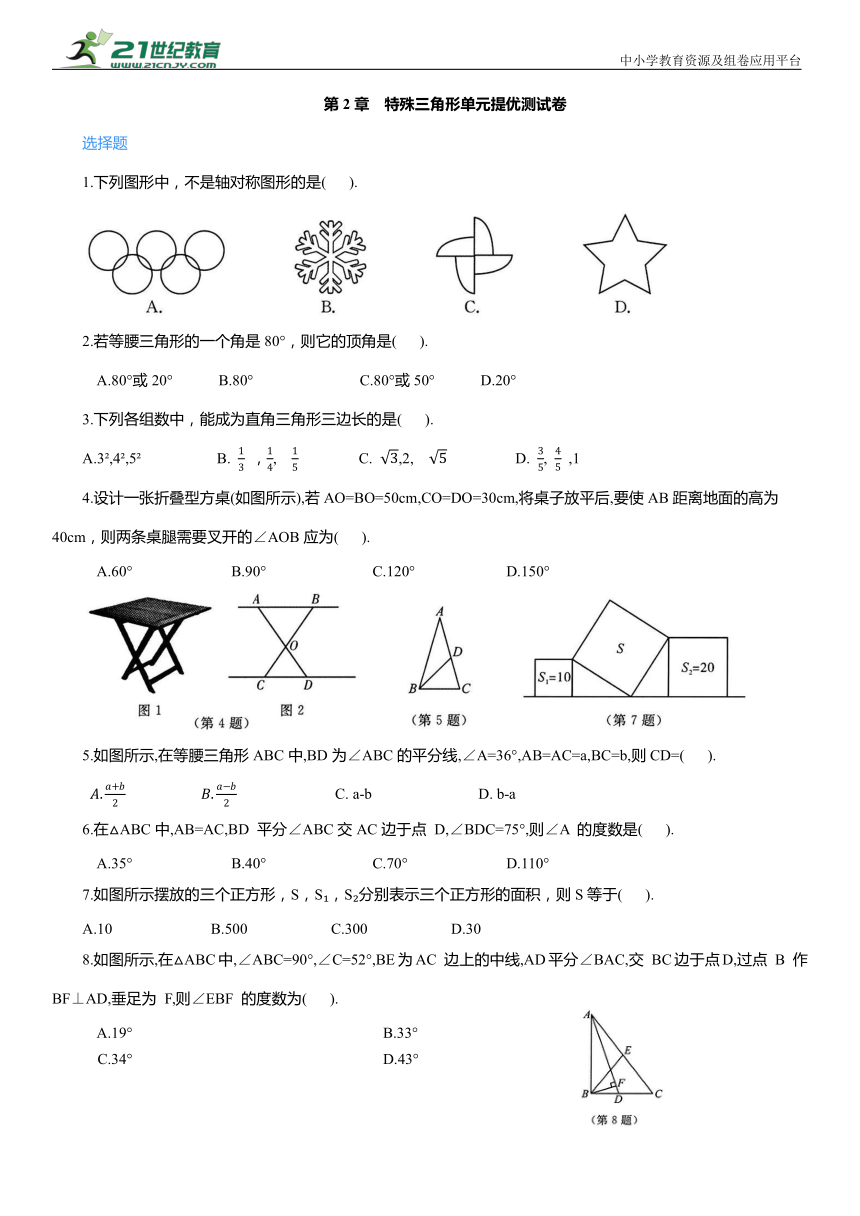 | |
| 格式 | docx | ||
| 文件大小 | 410.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-25 14:14:47 | ||
图片预览




文档简介
第2章 特殊三角形单元提优测试卷
选择题
1.下列图形中,不是轴对称图形的是( ).
2.若等腰三角形的一个角是80°,则它的顶角是( ).
A.80°或20° B.80° C.80°或50° D.20°
3.下列各组数中,能成为直角三角形三边长的是( ).
A.3 ,4 ,5 B. ,, C. ,2, D. , ,1
4.设计一张折叠型方桌(如图所示),若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( ).
A.60° B.90° C.120° D.150°
5.如图所示,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( ).
C. a-b D. b-a
6.在△ABC中,AB=AC,BD 平分∠ABC交AC边于点 D,∠BDC=75°,则∠A 的度数是( ).
A.35° B.40° C.70° D.110°
7.如图所示摆放的三个正方形,S,S ,S 分别表示三个正方形的面积,则S等于( ).
A.10 B.500 C.300 D.30
8.如图所示,在△ABC中,∠ABC=90°,∠C=52°,BE为AC 边上的中线,AD平分∠BAC,交 BC边于点D,过点 B 作BF⊥AD,垂足为 F,则∠EBF 的度数为( ).
A.19° B.33°
C.34° D.43°
9.已知直角三角形纸片的两条直角边长分别为m和n(mA. m +2mn+n =0 B. m -2mn+n =0
C. m +2mn--n =0
10.如图所示,在等腰直角三角形ABC中,AC=AB,BD⊥AH于点D,CH⊥AH于点H,HE,DF分别平分∠AHC 和∠ADB,给出下列结论:①△AHC≌△BDA;②DF⊥HE;③DF=HE;④AE=BF.其中正确的是( ).
A.①③④ B.①
C.①②③ D.①②③④
填空题
11.若一个三角形的三个内角的比为1:2:3,则这个三角形的三边之比为 .
12.如图所示,在△ABC中,点 D 在边 BC上,AB=AD=DC,∠C=35°,则∠BAD= 度.
13.如图所示,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB= cm.
14.如图所示,在 Rt△ABC中,∠BAC=90°,AD⊥BC,AE是BC 边上的中线.①若∠C=40°,则∠DAE= ;②若∠DAE=20°,则∠C= .
15.如图所示,在 Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点 D 从点A 出发,以1cm/s的速度沿射线AC运动,当t= 时,△ABD为等腰三角形.
16.如图所示,在等腰直角三角形ABC中,∠BAC=90°,AC=AB,以AB为斜边在△ABC内部作Rt△ABD,连结CD,若∠ADC=135°,S△ABD=9,则线段AD 的长为 .
三解答题
17.如图所示为由三个阴影的小正方形组成的图形,请你在三个网格图中,各补画出一个有阴影的小正方形,使补画后的图形为轴对称图形.
18.在一次数学课上,陈老师在黑板上画出下图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推断出△AED 是等腰三角形.
(1)请你按陈老师的要求写出所有可能的条件: .
(2)任选一种证明.
已知: .(填序号)
求证:△AED是等腰三角形.
证明:
19.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形按如图所示的方式摆放时(其中 ,就可以用“面积法”来证明勾股定理,即证明 请你写出勾股定理的证明过程.
20.如图所示,∠ABC的平分线BF 与△ABC中∠ACB 的相邻外角. 的平分线CF 相交于点F,过点 F作DF∥BC,交AB 于点D,交AC于点E.
(1)写出图中的等腰三角形并说明理由.
(2)若BD=8cm,DE=3cm,求CE的长.
21.如图1所示,P是等腰三角形ABC 底边BC 上的一个动点,过点 P 作BC 的垂线,交直线AB 于点Q,交 CA 的延长线于点 R.
(1)请观察 AR 与AQ,猜想它们有何关系,并证明你的猜想.
(2)如果点 P 沿着底边BC 所在的直线,按由点 C 向点 B 的方向运动到CB 的延长线上时,(1)中所得的结论还成立吗 请你在图2中完成图形,并给予证明.
22.如图所示,△ABC与△DEF 是两个全等的等腰直角三角形, 现将△DEF 与△ABC 按如图所示的方式叠放在一起, 保持不动,△DEF运动,且满足:点E在边BC 上运动(点 E不与点B,C重合),且边 DE 始终经过点A,EF与AC交于点M.在△DEF 运动的过程中,△AEM能否构成等腰三角形 若能,请求出 BE 的长;若不能,请说明理由.
23.如图所示,在△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点 P 从点C 开始,按C→A→B→C的路径运动,且速度为1cm/s,设出发的时间为t(s).
(1)出发2s后,求△ABP 的周长.
(2)当t为何值时,△BCP 为等腰三角形
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为2cm/s,若 P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分
1. C 2. A 3. D 4. C 5. C 6. B 7. D 8. B9. C 10. D 11.1: :2 12.40 13.614.10°35° 15.5或6或
16.3 【解析】如答图所示,将△ADC 绕点 A 顺时针旋转90°得到△AEB,连结 ED,∴∠EAD=90°,AE=AD,∠AEB=∠ADC=135°.∴△AED是等腰直角三角形.∴∠AED=∠ADE=45°.
∵∠ADB=90°,∴∠BDE=45°.
∴△BED 是等腰直角三角形.
设AD=AE=x,则.
即 解得 (舍去).
∴AD=3.故答案为:3.
17.如答图所示.
18.(1)①③或①④或②③或②④.
(2)选②③证明.
∵∠AEB=∠DEC,BE=CE,∠B=∠C,
∴△ABE≌△DCE.∴AE=DE.∴AED为等腰三角形.
19.如答图所示,连结 BD,过点 B 作 DE 边上的高线BF,则BF=b--a.
又 a),
20.(1)图中有 2 个等腰三角形,即△BDF 和△CEF.
∵BF,CF分别平分∠ABC,∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG.
∵DF∥BC,∴∠DFB=∠CBF,∠EFC=∠FCG.
∴∠DBF=∠DFB,∠FCE=∠EFC.
∴BD=FD,EF=CE.
∴△BDF 和△CEF为等腰三角形.
(2)∵DF=BD=8cm,DE=3cm,
∴EF=DF--DE=5(cm).∴CE=5cm.
21.(1)AR=AQ,理由如下:
∵AB=AC,∴∠B=∠C.
∵RP⊥BC,∴∠B+∠BQP=∠C+∠R=90°.
∴∠BQP = ∠R. ∵ ∠BQP = ∠AQR, ∴∠R =∠AQR.∴AR=AQ.
(2)如答图所示,猜想仍然成立.理由如下:
∵AB=AC,∴∠ABC=∠C.
∵∠ABC=∠PBQ,∴∠PBQ=∠C.
∵RP⊥BC,∴∠PBQ+∠BQP=∠C+∠R=90°.
∴∠BQP=∠R.∴AR=AQ.
22.①若AE=AM,则∠AME=∠AEM=45°.
∵∠C=45°,∴∠AME=∠C.
又∵∠AME>∠C,∴这种情况不成立.
②若AE=EM,∵∠B=∠AEM=45°.
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°.∴∠BAE=∠MEC.
在△ABE 和△ECM中,∵
∴△ABE≌△ECM,∴CE=AB=
③若MA=ME,则∠MAE=∠AEM=45°,
∵∠BAC=90°,∴∠BAE=45°.
∴AE平分∠BAC.∵AB=AC,∴BE= BC=1.
23.(1)如答图1所示,∵∠C=90°,AB=5cm,BC=3cm,∴AC=4cm.
中小学教育资源及组卷应用平台
∵动点 P 从点C 开始,按C→A→B→C的路径运动,且速度为1cm/s,∴出发2s后,CP=2cm.
∴△ABP 的周长为
(2)①如答图2 所示,当点 P 在AC 上时,BC=CP=3cm,∴t=3时,△BCP 为等腰三角形.
②当点 P 在AB 上时,有三种情况:
i)如答图3 所示,若 BP=CB=3cm,此时 AP=2cm,点 P 运动的路程为2+4=6(cm),
∴t=6时,△BCP 为等腰三角形;
ii)如答图 4 所示,若 CP=BC=3cm,过点 C 作CD⊥AB于点 D,
根据面积法求得
在 Rt△PCD中, =1.8(cm),
∴BP=2PD=3.6cm,点 P 运动的路程为9--3.6=5.4(cm).
∴t=5.4时,△BCP 为等腰三角形.
iii)如答图5所示,若BP=CP,此时 P应该为斜边AB的中点,点 P 运动的路程为4+2.5=6.5(cm).
∴t=6.5时,△BCP 为等腰三角形.
综上所述,当t为3,5.4,6 或6.5 时,△BCP 为等腰三角形.
(3)如答图6所示,当点 P 在AC 上,点 Q在AB 上时,则 PC=t,BQ=2t-3.
∵直线 PQ把△ABC的周长分成相等的两部分,
∴t+2t-3+3=6,解得t=2.
如答图7 所示,当点 P 在AB上,点 Q在AC上时,则AP=t-4,AQ=2t-8.
∵直线 PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,解得t=6.
∴当t为2 或6 时,直线 PQ把△ABC的周长分成相等的两部分.
选择题
1.下列图形中,不是轴对称图形的是( ).
2.若等腰三角形的一个角是80°,则它的顶角是( ).
A.80°或20° B.80° C.80°或50° D.20°
3.下列各组数中,能成为直角三角形三边长的是( ).
A.3 ,4 ,5 B. ,, C. ,2, D. , ,1
4.设计一张折叠型方桌(如图所示),若AO=BO=50cm,CO=DO=30cm,将桌子放平后,要使AB距离地面的高为40cm,则两条桌腿需要叉开的∠AOB应为( ).
A.60° B.90° C.120° D.150°
5.如图所示,在等腰三角形ABC中,BD为∠ABC的平分线,∠A=36°,AB=AC=a,BC=b,则CD=( ).
C. a-b D. b-a
6.在△ABC中,AB=AC,BD 平分∠ABC交AC边于点 D,∠BDC=75°,则∠A 的度数是( ).
A.35° B.40° C.70° D.110°
7.如图所示摆放的三个正方形,S,S ,S 分别表示三个正方形的面积,则S等于( ).
A.10 B.500 C.300 D.30
8.如图所示,在△ABC中,∠ABC=90°,∠C=52°,BE为AC 边上的中线,AD平分∠BAC,交 BC边于点D,过点 B 作BF⊥AD,垂足为 F,则∠EBF 的度数为( ).
A.19° B.33°
C.34° D.43°
9.已知直角三角形纸片的两条直角边长分别为m和n(m
C. m +2mn--n =0
10.如图所示,在等腰直角三角形ABC中,AC=AB,BD⊥AH于点D,CH⊥AH于点H,HE,DF分别平分∠AHC 和∠ADB,给出下列结论:①△AHC≌△BDA;②DF⊥HE;③DF=HE;④AE=BF.其中正确的是( ).
A.①③④ B.①
C.①②③ D.①②③④
填空题
11.若一个三角形的三个内角的比为1:2:3,则这个三角形的三边之比为 .
12.如图所示,在△ABC中,点 D 在边 BC上,AB=AD=DC,∠C=35°,则∠BAD= 度.
13.如图所示,AB=AC,DB=DC,若∠ABC为60°,BE=3cm,则AB= cm.
14.如图所示,在 Rt△ABC中,∠BAC=90°,AD⊥BC,AE是BC 边上的中线.①若∠C=40°,则∠DAE= ;②若∠DAE=20°,则∠C= .
15.如图所示,在 Rt△ABC中,∠ACB=90°,AB=5cm,BC=4cm.动点 D 从点A 出发,以1cm/s的速度沿射线AC运动,当t= 时,△ABD为等腰三角形.
16.如图所示,在等腰直角三角形ABC中,∠BAC=90°,AC=AB,以AB为斜边在△ABC内部作Rt△ABD,连结CD,若∠ADC=135°,S△ABD=9,则线段AD 的长为 .
三解答题
17.如图所示为由三个阴影的小正方形组成的图形,请你在三个网格图中,各补画出一个有阴影的小正方形,使补画后的图形为轴对称图形.
18.在一次数学课上,陈老师在黑板上画出下图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推断出△AED 是等腰三角形.
(1)请你按陈老师的要求写出所有可能的条件: .
(2)任选一种证明.
已知: .(填序号)
求证:△AED是等腰三角形.
证明:
19.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形按如图所示的方式摆放时(其中 ,就可以用“面积法”来证明勾股定理,即证明 请你写出勾股定理的证明过程.
20.如图所示,∠ABC的平分线BF 与△ABC中∠ACB 的相邻外角. 的平分线CF 相交于点F,过点 F作DF∥BC,交AB 于点D,交AC于点E.
(1)写出图中的等腰三角形并说明理由.
(2)若BD=8cm,DE=3cm,求CE的长.
21.如图1所示,P是等腰三角形ABC 底边BC 上的一个动点,过点 P 作BC 的垂线,交直线AB 于点Q,交 CA 的延长线于点 R.
(1)请观察 AR 与AQ,猜想它们有何关系,并证明你的猜想.
(2)如果点 P 沿着底边BC 所在的直线,按由点 C 向点 B 的方向运动到CB 的延长线上时,(1)中所得的结论还成立吗 请你在图2中完成图形,并给予证明.
22.如图所示,△ABC与△DEF 是两个全等的等腰直角三角形, 现将△DEF 与△ABC 按如图所示的方式叠放在一起, 保持不动,△DEF运动,且满足:点E在边BC 上运动(点 E不与点B,C重合),且边 DE 始终经过点A,EF与AC交于点M.在△DEF 运动的过程中,△AEM能否构成等腰三角形 若能,请求出 BE 的长;若不能,请说明理由.
23.如图所示,在△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点 P 从点C 开始,按C→A→B→C的路径运动,且速度为1cm/s,设出发的时间为t(s).
(1)出发2s后,求△ABP 的周长.
(2)当t为何值时,△BCP 为等腰三角形
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为2cm/s,若 P,Q两点同时出发,当P,Q中有一点到达终点时,另一点也停止运动.当t为何值时,直线PQ把△ABC的周长分成相等的两部分
1. C 2. A 3. D 4. C 5. C 6. B 7. D 8. B9. C 10. D 11.1: :2 12.40 13.614.10°35° 15.5或6或
16.3 【解析】如答图所示,将△ADC 绕点 A 顺时针旋转90°得到△AEB,连结 ED,∴∠EAD=90°,AE=AD,∠AEB=∠ADC=135°.∴△AED是等腰直角三角形.∴∠AED=∠ADE=45°.
∵∠ADB=90°,∴∠BDE=45°.
∴△BED 是等腰直角三角形.
设AD=AE=x,则.
即 解得 (舍去).
∴AD=3.故答案为:3.
17.如答图所示.
18.(1)①③或①④或②③或②④.
(2)选②③证明.
∵∠AEB=∠DEC,BE=CE,∠B=∠C,
∴△ABE≌△DCE.∴AE=DE.∴AED为等腰三角形.
19.如答图所示,连结 BD,过点 B 作 DE 边上的高线BF,则BF=b--a.
又 a),
20.(1)图中有 2 个等腰三角形,即△BDF 和△CEF.
∵BF,CF分别平分∠ABC,∠ACG,
∴∠DBF=∠CBF,∠FCE=∠FCG.
∵DF∥BC,∴∠DFB=∠CBF,∠EFC=∠FCG.
∴∠DBF=∠DFB,∠FCE=∠EFC.
∴BD=FD,EF=CE.
∴△BDF 和△CEF为等腰三角形.
(2)∵DF=BD=8cm,DE=3cm,
∴EF=DF--DE=5(cm).∴CE=5cm.
21.(1)AR=AQ,理由如下:
∵AB=AC,∴∠B=∠C.
∵RP⊥BC,∴∠B+∠BQP=∠C+∠R=90°.
∴∠BQP = ∠R. ∵ ∠BQP = ∠AQR, ∴∠R =∠AQR.∴AR=AQ.
(2)如答图所示,猜想仍然成立.理由如下:
∵AB=AC,∴∠ABC=∠C.
∵∠ABC=∠PBQ,∴∠PBQ=∠C.
∵RP⊥BC,∴∠PBQ+∠BQP=∠C+∠R=90°.
∴∠BQP=∠R.∴AR=AQ.
22.①若AE=AM,则∠AME=∠AEM=45°.
∵∠C=45°,∴∠AME=∠C.
又∵∠AME>∠C,∴这种情况不成立.
②若AE=EM,∵∠B=∠AEM=45°.
∴∠BAE+∠AEB=135°,∠MEC+∠AEB=135°.∴∠BAE=∠MEC.
在△ABE 和△ECM中,∵
∴△ABE≌△ECM,∴CE=AB=
③若MA=ME,则∠MAE=∠AEM=45°,
∵∠BAC=90°,∴∠BAE=45°.
∴AE平分∠BAC.∵AB=AC,∴BE= BC=1.
23.(1)如答图1所示,∵∠C=90°,AB=5cm,BC=3cm,∴AC=4cm.
中小学教育资源及组卷应用平台
∵动点 P 从点C 开始,按C→A→B→C的路径运动,且速度为1cm/s,∴出发2s后,CP=2cm.
∴△ABP 的周长为
(2)①如答图2 所示,当点 P 在AC 上时,BC=CP=3cm,∴t=3时,△BCP 为等腰三角形.
②当点 P 在AB 上时,有三种情况:
i)如答图3 所示,若 BP=CB=3cm,此时 AP=2cm,点 P 运动的路程为2+4=6(cm),
∴t=6时,△BCP 为等腰三角形;
ii)如答图 4 所示,若 CP=BC=3cm,过点 C 作CD⊥AB于点 D,
根据面积法求得
在 Rt△PCD中, =1.8(cm),
∴BP=2PD=3.6cm,点 P 运动的路程为9--3.6=5.4(cm).
∴t=5.4时,△BCP 为等腰三角形.
iii)如答图5所示,若BP=CP,此时 P应该为斜边AB的中点,点 P 运动的路程为4+2.5=6.5(cm).
∴t=6.5时,△BCP 为等腰三角形.
综上所述,当t为3,5.4,6 或6.5 时,△BCP 为等腰三角形.
(3)如答图6所示,当点 P 在AC 上,点 Q在AB 上时,则 PC=t,BQ=2t-3.
∵直线 PQ把△ABC的周长分成相等的两部分,
∴t+2t-3+3=6,解得t=2.
如答图7 所示,当点 P 在AB上,点 Q在AC上时,则AP=t-4,AQ=2t-8.
∵直线 PQ把△ABC的周长分成相等的两部分,
∴t-4+2t-8=6,解得t=6.
∴当t为2 或6 时,直线 PQ把△ABC的周长分成相等的两部分.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
