2.4 等腰三角形的判定定理同步练习(含答案)
文档属性
| 名称 | 2.4 等腰三角形的判定定理同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.4 等腰三角形的判定定理
1.下列条件中,不能判定△ABC是等腰三角形的是( ).
A. a=3,b=3,c=4 B. a:b:c=2:3:4
C.∠B=50°,∠C=80° D.∠A:∠B:∠C=1:1:2
2.小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一条直线上,则图中等腰三角形的个数是( ).
A.4 B.3
C.2 D.1
3.如图所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线相交于点D,过点 D 作直线EF∥BC,交AB于点E,交AC于点F,则图中等腰三角形共有( ).
A.3个 B.4个 C.5个 D.6个
4.如图所示,△ABC的面积为1cm ,BP平分∠ABC,AP⊥BP 于点 P,则△PBC的面积为( ).
A.0.4cm B.0.5cm D.0.7cm
5.在△ABC中,∠A=100°,当∠B= 时,△ABC是等腰三角形.
6.如图所示,在△ABC中,D,E分别为AC,AB上的点,BD与CE 交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件组合可判定△ABC是等腰三角形 答: .(用序号写出一种情形)
7.如图所示,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5cm,CE=3cm,则△CDE 的周长是 .
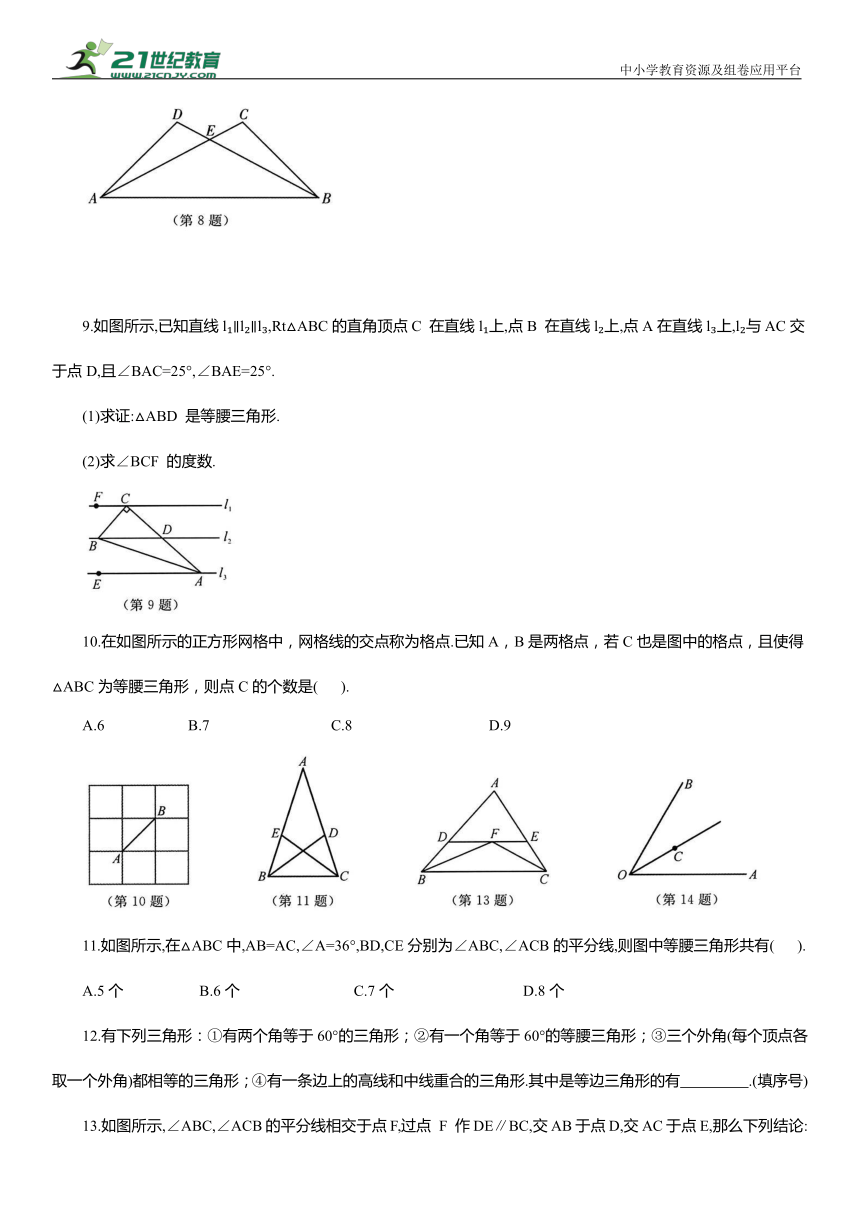
8.如图所示,AD=BC,AC=BD,求证:△EAB是等腰三角形.
9.如图所示,已知直线l ∥l ∥l ,Rt△ABC的直角顶点C 在直线l 上,点B 在直线l 上,点A在直线l 上,l 与AC交于点D,且∠BAC=25°,∠BAE=25°.
(1)求证:△ABD 是等腰三角形.
(2)求∠BCF 的度数.
10.在如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,若C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( ).
A.6 B.7 C.8 D.9
11.如图所示,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的平分线,则图中等腰三角形共有( ).
A.5个 B.6个 C.7个 D.8个
12.有下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点各取一个外角)都相等的三角形;④有一条边上的高线和中线重合的三角形.其中是等边三角形的有 .(填序号)
13.如图所示,∠ABC,∠ACB的平分线相交于点F,过点 F 作DE∥BC,交AB于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是 .(填序号)
14.如图所示,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E 满足△OCE 是等腰三角形,那么∠OEC的度数为 .
15.如图所示,△ABC为等边三角形,D为BC 延长线上的一点,CE平分∠ACD,CE=BD.求证:△ADE 为等边三角形.
16.如图所示,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF 是等腰三角形.
(2)当∠A=40°时,求∠DEF的度数.
17.如图所示,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ).
A.4 B.5
C.6 D.7
18.如图所示,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE 是等腰三角形.
19.如图所示,在 中,AD为∠BAC的平分线,BP⊥AD,垂足为 P.已知AB=5,BP=2,AC=9,试说明:∠ABC=3∠C.
2.4 等腰三角形的判定定理
1. B 2. B 3. C 4. B 5.40° 6.①③(答案不唯一) 7.13cm
8.在△ADB和△BCA中,
∴△ADB≌△BCA(SSS).∴∠DBA=∠CAB.
∴AE=BE.∴△EAB 是等腰三角形.
9.(1)∵l ∥l ,∴∠ABD=∠BAE=25°.
∵∠BAC=25°,∴∠ABD=∠BAC.
∴△ABD是等腰三角形.
(2)∵∠BAC=25°,∠ACB=90°,
∴∠CBD=∠ABC--∠ABD=65°-25°=40°.
∵l ∥l ,∴∠BCF=∠CBD=40°.
10. C 11. D 12.①②③ 13.①②③
14.120°或 75°或 30°
15.∵△ABC为等边三角形,
∴∠B=∠ACB=60°,AB=AC.∴∠ACD=120°.
∵CE平分∠ACD,∴∠ACE=∠DCE=60°.
∴∠B=∠ACE.
在△ABD 和△ACE中,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠BAD--∠CAD=∠CAE-∠CAD,即∠BAC=∠DAE.∵∠BAC=60°,∴∠DAE=60°.
∴△ADE为等边三角形.
16.(1)∵AB=AC,∴∠ABC=∠ACB.
在△DBE和△ECF中,
∴△DBE≌△ECF.∴DE=EF.
∴△DEF是等腰三角形.
(2)∵△DBE≌△ECF.
∴∠BDE=∠CEF,∠BED=∠CFE.
∵∠A+∠B+∠C=180°,且∠B=∠C,∠A=40°.
∴∠B=70°.∴∠BDE+∠BED=110°.
∴∠CEF+∠BED=110°.∴∠DEF=70°.
17. D
18.∵DE∥AC,∴∠CAD=∠ADE.
∵AD平分∠BAC,∴∠CAD=∠DAE.
∴∠DAE=∠ADE.
∵AD⊥BD,∴∠DAE+∠B = 90°,∠ADE+∠BDE=90°.
∴∠B=∠BDE.∴△BDE是等腰三角形.
19.如答图所示,延长 BP,交 AC于点 E.
∵AD平分∠BAC,BP⊥AD,
∴∠BAP=∠EAP,∠APB=∠APE.
又∵AP=AP,∴△ABP≌△AEP.
∴BP=PE,AE=AB,∠AEB=∠ABE.
∴BE=BP+PE=4,AE=AB=5.
∴CE=AC-AE=9-5=4.∴CE=BE.
∴∠EBC=∠C.
又∵∠ABE=∠AEB=∠C+∠EBC,∴∠ABE=2∠C.∴∠ABC=∠ABE+∠EBC=3∠C.
2.4 等腰三角形的判定定理
1.下列条件中,不能判定△ABC是等腰三角形的是( ).
A. a=3,b=3,c=4 B. a:b:c=2:3:4
C.∠B=50°,∠C=80° D.∠A:∠B:∠C=1:1:2
2.小明将两个全等且有一个角为60°的直角三角形拼成如图所示的图形,其中两条较长直角边在同一条直线上,则图中等腰三角形的个数是( ).
A.4 B.3
C.2 D.1
3.如图所示,在△ABC中,AB=AC,∠ABC,∠ACB的平分线相交于点D,过点 D 作直线EF∥BC,交AB于点E,交AC于点F,则图中等腰三角形共有( ).
A.3个 B.4个 C.5个 D.6个
4.如图所示,△ABC的面积为1cm ,BP平分∠ABC,AP⊥BP 于点 P,则△PBC的面积为( ).
A.0.4cm B.0.5cm D.0.7cm
5.在△ABC中,∠A=100°,当∠B= 时,△ABC是等腰三角形.
6.如图所示,在△ABC中,D,E分别为AC,AB上的点,BD与CE 交于点O.给出下列三个条件:①∠EBO=∠DCO;②∠BEO=∠CDO;③BE=CD.上述三个条件中,哪两个条件组合可判定△ABC是等腰三角形 答: .(用序号写出一种情形)
7.如图所示,在△ABC中,AB=AC,D,E两点分别在AC,BC上,BD是∠ABC的平分线,DE∥AB.若BE=5cm,CE=3cm,则△CDE 的周长是 .
8.如图所示,AD=BC,AC=BD,求证:△EAB是等腰三角形.
9.如图所示,已知直线l ∥l ∥l ,Rt△ABC的直角顶点C 在直线l 上,点B 在直线l 上,点A在直线l 上,l 与AC交于点D,且∠BAC=25°,∠BAE=25°.
(1)求证:△ABD 是等腰三角形.
(2)求∠BCF 的度数.
10.在如图所示的正方形网格中,网格线的交点称为格点.已知A,B是两格点,若C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( ).
A.6 B.7 C.8 D.9
11.如图所示,在△ABC中,AB=AC,∠A=36°,BD,CE分别为∠ABC,∠ACB的平分线,则图中等腰三角形共有( ).
A.5个 B.6个 C.7个 D.8个
12.有下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点各取一个外角)都相等的三角形;④有一条边上的高线和中线重合的三角形.其中是等边三角形的有 .(填序号)
13.如图所示,∠ABC,∠ACB的平分线相交于点F,过点 F 作DE∥BC,交AB于点D,交AC于点E,那么下列结论:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.其中正确的是 .(填序号)
14.如图所示,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E 满足△OCE 是等腰三角形,那么∠OEC的度数为 .
15.如图所示,△ABC为等边三角形,D为BC 延长线上的一点,CE平分∠ACD,CE=BD.求证:△ADE 为等边三角形.
16.如图所示,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
(1)求证:△DEF 是等腰三角形.
(2)当∠A=40°时,求∠DEF的度数.
17.如图所示,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( ).
A.4 B.5
C.6 D.7
18.如图所示,AD平分∠BAC,AD⊥BD,垂足为D,DE∥AC.求证:△BDE 是等腰三角形.
19.如图所示,在 中,AD为∠BAC的平分线,BP⊥AD,垂足为 P.已知AB=5,BP=2,AC=9,试说明:∠ABC=3∠C.
2.4 等腰三角形的判定定理
1. B 2. B 3. C 4. B 5.40° 6.①③(答案不唯一) 7.13cm
8.在△ADB和△BCA中,
∴△ADB≌△BCA(SSS).∴∠DBA=∠CAB.
∴AE=BE.∴△EAB 是等腰三角形.
9.(1)∵l ∥l ,∴∠ABD=∠BAE=25°.
∵∠BAC=25°,∴∠ABD=∠BAC.
∴△ABD是等腰三角形.
(2)∵∠BAC=25°,∠ACB=90°,
∴∠CBD=∠ABC--∠ABD=65°-25°=40°.
∵l ∥l ,∴∠BCF=∠CBD=40°.
10. C 11. D 12.①②③ 13.①②③
14.120°或 75°或 30°
15.∵△ABC为等边三角形,
∴∠B=∠ACB=60°,AB=AC.∴∠ACD=120°.
∵CE平分∠ACD,∴∠ACE=∠DCE=60°.
∴∠B=∠ACE.
在△ABD 和△ACE中,
∴△ABD≌△ACE.
∴AD=AE,∠BAD=∠CAE.
∴∠BAD--∠CAD=∠CAE-∠CAD,即∠BAC=∠DAE.∵∠BAC=60°,∴∠DAE=60°.
∴△ADE为等边三角形.
16.(1)∵AB=AC,∴∠ABC=∠ACB.
在△DBE和△ECF中,
∴△DBE≌△ECF.∴DE=EF.
∴△DEF是等腰三角形.
(2)∵△DBE≌△ECF.
∴∠BDE=∠CEF,∠BED=∠CFE.
∵∠A+∠B+∠C=180°,且∠B=∠C,∠A=40°.
∴∠B=70°.∴∠BDE+∠BED=110°.
∴∠CEF+∠BED=110°.∴∠DEF=70°.
17. D
18.∵DE∥AC,∴∠CAD=∠ADE.
∵AD平分∠BAC,∴∠CAD=∠DAE.
∴∠DAE=∠ADE.
∵AD⊥BD,∴∠DAE+∠B = 90°,∠ADE+∠BDE=90°.
∴∠B=∠BDE.∴△BDE是等腰三角形.
19.如答图所示,延长 BP,交 AC于点 E.
∵AD平分∠BAC,BP⊥AD,
∴∠BAP=∠EAP,∠APB=∠APE.
又∵AP=AP,∴△ABP≌△AEP.
∴BP=PE,AE=AB,∠AEB=∠ABE.
∴BE=BP+PE=4,AE=AB=5.
∴CE=AC-AE=9-5=4.∴CE=BE.
∴∠EBC=∠C.
又∵∠ABE=∠AEB=∠C+∠EBC,∴∠ABE=2∠C.∴∠ABC=∠ABE+∠EBC=3∠C.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
