2.3 等腰三角形的性质定理(2) 同步练习(含答案)
文档属性
| 名称 | 2.3 等腰三角形的性质定理(2) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
2.3 等腰三角形的性质定理(2)
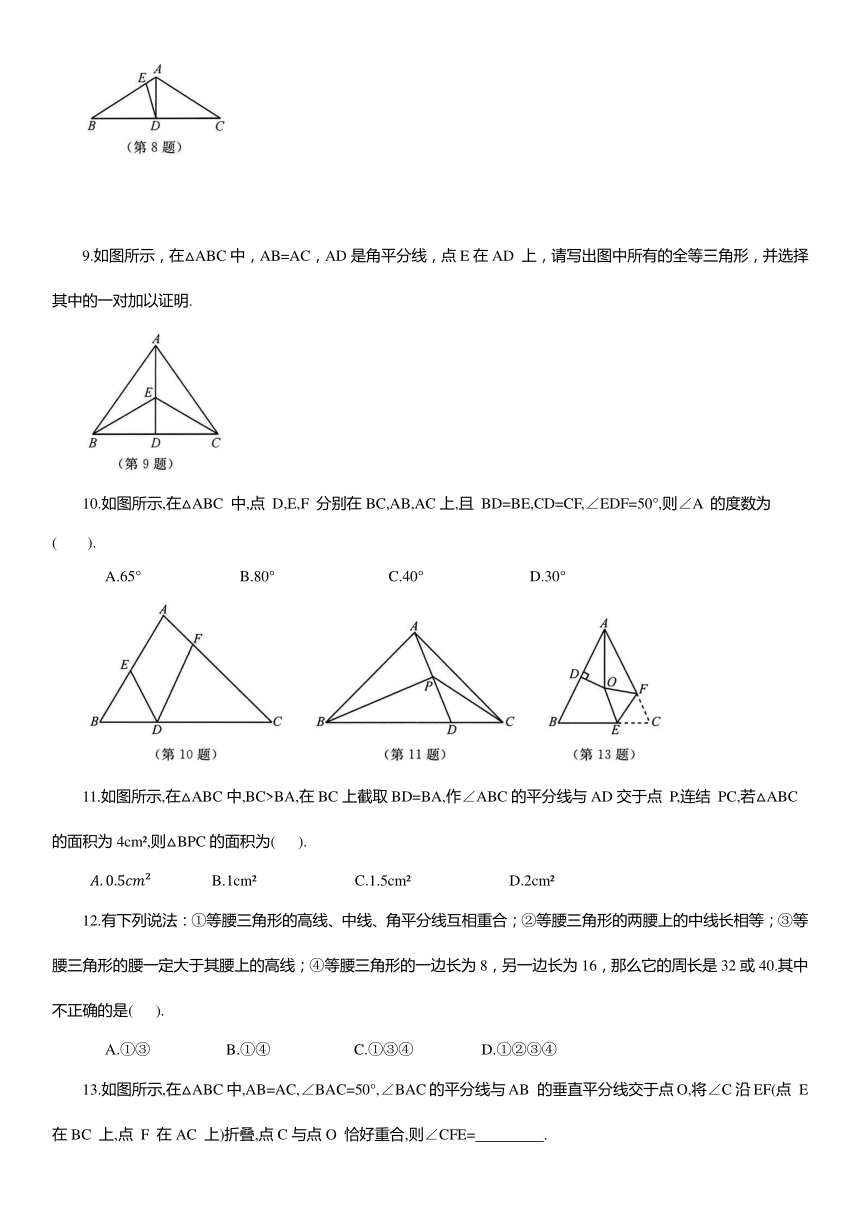
1.如图所示,在△ABC中,AB=AC,D是BC的中点.下列结论中,不正确的是( ).
A.∠B=∠C B. AD⊥BC C. AD平分∠BAC D. AB=2BD
2.如图所示,在△ABC中,AB=AC,AD是BC 边上的高线,E,F是AD 的三等分点,若△ABC的面积为12,则图中△BEF 的面积为( ).
A.2 B.3 C.4 D.6
3.如图所示,在△ABC中,AB=AC,∠A=34°,线段AB 的垂直平分线交AB 于点D,交AC于点E,连结 BE,则∠CBE的度数为( ).
A.39° B.40° C.45° D.46°
4.如图所示,AD,CE 分别是△ABC 的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( ).
A.25° B.50° C.32.5° D.65°
5.如图所示,在△ABC 中,AB=AC,AD⊥BC 于点 D,若∠BAD=20°,则∠BAC=
6.如图所示,△ABC的周长为16,且AB=AC,AD⊥BC于点D,△ACD的周长为12,那么AD 的长为 .
7.如图所示,△ABC为等边三角形,BD⊥AB,BD=AB,则∠DCB= .
8.如图所示,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,E是AB 上一点,且BD=BE,求∠ADE的度数.
9.如图所示,在△ABC中,AB=AC,AD是角平分线,点E在AD 上,请写出图中所有的全等三角形,并选择其中的一对加以证明.
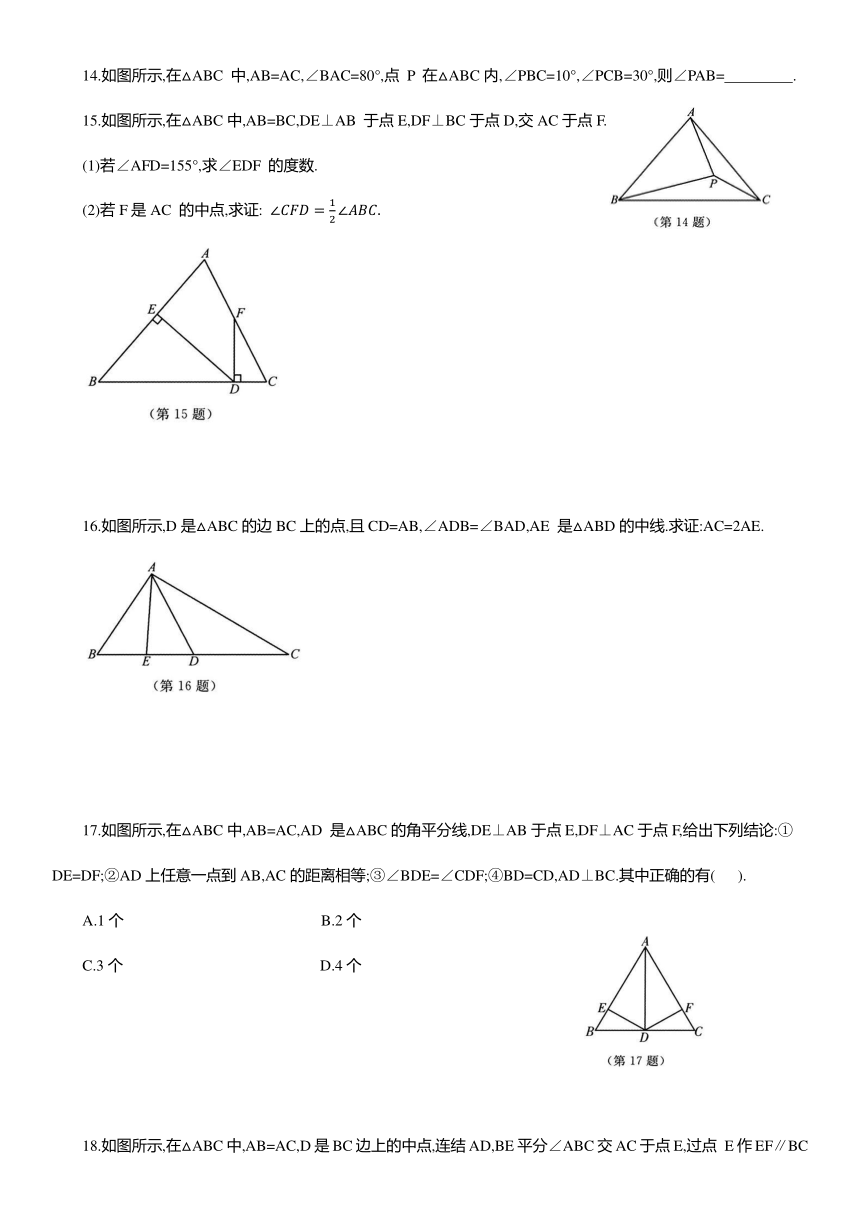
10.如图所示,在△ABC 中,点 D,E,F 分别在BC,AB,AC上,且 BD=BE,CD=CF,∠EDF=50°,则∠A 的度数为( ).
A.65° B.80° C.40° D.30°
11.如图所示,在△ABC中,BC>BA,在BC上截取BD=BA,作∠ABC的平分线与AD交于点 P,连结 PC,若△ABC的面积为4cm ,则△BPC的面积为( ).
B.1cm C.1.5cm D.2cm
12.有下列说法:①等腰三角形的高线、中线、角平分线互相重合;②等腰三角形的两腰上的中线长相等;③等腰三角形的腰一定大于其腰上的高线;④等腰三角形的一边长为8,另一边长为16,那么它的周长是32或40.其中不正确的是( ).
A.①③ B.①④ C.①③④ D.①②③④
13.如图所示,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB 的垂直平分线交于点O,将∠C沿EF(点 E 在BC 上,点 F 在AC 上)折叠,点C与点O 恰好重合,则∠CFE= .
14.如图所示,在△ABC 中,AB=AC,∠BAC=80°,点 P 在△ABC内,∠PBC=10°,∠PCB=30°,则∠PAB= .
15.如图所示,在△ABC中,AB=BC,DE⊥AB 于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF 的度数.
(2)若F是AC 的中点,求证:
16.如图所示,D是△ABC的边BC上的点,且CD=AB,∠ADB=∠BAD,AE 是△ABD的中线.求证:AC=2AE.
17.如图所示,在△ABC中,AB=AC,AD 是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,给出下列结论:①DE=DF;②AD上任意一点到AB,AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
18.如图所示,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点 E作EF∥BC交AB 于点 F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
19.在△ABC中,AC=BC,∠ACB=120°,D为AB 边的中点,∠EDF=60°,DE,DF分别交AC,BC于点E,F.
(1)如图1所示,若EF∥AB,求证:DE=DF.
(2)如图2所示,若EF与AB 不平行,则第(1)题的结论是否成立 请说明理由.
2.3 等腰三角形的性质定理(2)
1. D 2. A 3. A 4. C 5.40° 6.4 7.15°
8.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵BD=BE,∴∠BDE=∠BED=75°.
∵AB=AC,AD是BC边上的中线,∴∠ADB=90°.
∴∠ADE=∠ADB-∠BDE=15°.
9.△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.以△ABE≌△ACE 为例,证明如下:
∵AD平分∠BAC,∴∠BAE=∠CAE.在△ABE 和△ACE中, ∴△ABE≌△ACE(SAS).
10. B 11. D 12. C 13.65° 14.70°
15.(1)∵∠AFD=155°,∴∠DFC=25°.
∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°.
∵AB=BC,∴∠A=∠C=65°.
∴∠B=50°,∠BDE=40°.
(2)连结BF.∵AB=BC,且 F是AC 的中点,
∴∠CFD+∠BFD=90°.
∵∠CBF+∠BFD=90°,
∴∠CFD=∠CBF.∴∠CFD= ∠ABC.
16.如答图所示,延长 AE到点 F,使 EF=AE,连结 DF.
∵AE是△ABD的中线,∴BE=DE.
在△ABE和△FDE中,
∴△ABE≌△FDE(SAS).
∴AB=FD,∠BAE=∠DFE.
∵∠ADB 是△ADC的外角,
∴∠DAC+∠ACD=∠ADB.
∵∠ADB=∠BAD=∠BAE+∠DAE,∠BAE=∠DFE,∴∠DFE+∠DAE=∠DAC+∠ACD.
∴∠ADF=∠ADC. ∵AB=DC,∴DF=DC.
在△ADF 和△ADC中,
∴△ADF≌△ADC(SAS).∴AF=AC.
∵AF=AE+EF,AE=EF,∴AC=2AE.
17. D
18.(1)∵AB=AC,∴∠C=∠ABC.
∵∠C=36°,∴∠ABC=36°.
∵BD=CD,AB=AC,∴AD⊥BC.
∴∠ADB=90°.∴∠BAD=90°-36°=54°.
(2)∵BE平分∠ABC,
∵EF∥BC,∴∠FEB=∠CBE.
∴∠FBE=∠FEB.∴FB=FE.
19.(1)∵在△ABC中,AC=BC,∠ACB=120°,
∴∠A=∠B=30°.∵EF∥AB,
∴∠FEC=∠A=30°,∠EFC=∠B=30°.
∴CE=CF.
∵D是等腰三角形ABC 的边AB 的中点,
∴CD是角平分线,即∠DCE=∠DCF.
在△DCE 和△DCF中, ∴△DCE≌△DCF(SAS),∴DE=DF.
(2)如答图所示,过点 D 作 DM⊥AC 交AC 于点M,再作 DN⊥BC交BC 于点 N.
由(1)可知 DM=DN.∠MDN=180°--∠ADM-∠BDN= 60°,∠EDF = 60°,∴∠EDM= 60°-∠EDN,∠FDN = 60° - ∠EDN. ∴∠EDM =∠FDN.又∵∠DME=∠DNF=90°,DM=DN,∴△DEM≌△DFN(ASA).∴DE=DF.
2.3 等腰三角形的性质定理(2)
1.如图所示,在△ABC中,AB=AC,D是BC的中点.下列结论中,不正确的是( ).
A.∠B=∠C B. AD⊥BC C. AD平分∠BAC D. AB=2BD
2.如图所示,在△ABC中,AB=AC,AD是BC 边上的高线,E,F是AD 的三等分点,若△ABC的面积为12,则图中△BEF 的面积为( ).
A.2 B.3 C.4 D.6
3.如图所示,在△ABC中,AB=AC,∠A=34°,线段AB 的垂直平分线交AB 于点D,交AC于点E,连结 BE,则∠CBE的度数为( ).
A.39° B.40° C.45° D.46°
4.如图所示,AD,CE 分别是△ABC 的中线和角平分线,若AB=AC,∠CAD=25°,则∠ACE的度数是( ).
A.25° B.50° C.32.5° D.65°
5.如图所示,在△ABC 中,AB=AC,AD⊥BC 于点 D,若∠BAD=20°,则∠BAC=
6.如图所示,△ABC的周长为16,且AB=AC,AD⊥BC于点D,△ACD的周长为12,那么AD 的长为 .
7.如图所示,△ABC为等边三角形,BD⊥AB,BD=AB,则∠DCB= .
8.如图所示,在△ABC中,AB=AC,∠BAC=120°,AD是BC边上的中线,E是AB 上一点,且BD=BE,求∠ADE的度数.
9.如图所示,在△ABC中,AB=AC,AD是角平分线,点E在AD 上,请写出图中所有的全等三角形,并选择其中的一对加以证明.
10.如图所示,在△ABC 中,点 D,E,F 分别在BC,AB,AC上,且 BD=BE,CD=CF,∠EDF=50°,则∠A 的度数为( ).
A.65° B.80° C.40° D.30°
11.如图所示,在△ABC中,BC>BA,在BC上截取BD=BA,作∠ABC的平分线与AD交于点 P,连结 PC,若△ABC的面积为4cm ,则△BPC的面积为( ).
B.1cm C.1.5cm D.2cm
12.有下列说法:①等腰三角形的高线、中线、角平分线互相重合;②等腰三角形的两腰上的中线长相等;③等腰三角形的腰一定大于其腰上的高线;④等腰三角形的一边长为8,另一边长为16,那么它的周长是32或40.其中不正确的是( ).
A.①③ B.①④ C.①③④ D.①②③④
13.如图所示,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分线与AB 的垂直平分线交于点O,将∠C沿EF(点 E 在BC 上,点 F 在AC 上)折叠,点C与点O 恰好重合,则∠CFE= .
14.如图所示,在△ABC 中,AB=AC,∠BAC=80°,点 P 在△ABC内,∠PBC=10°,∠PCB=30°,则∠PAB= .
15.如图所示,在△ABC中,AB=BC,DE⊥AB 于点E,DF⊥BC于点D,交AC于点F.
(1)若∠AFD=155°,求∠EDF 的度数.
(2)若F是AC 的中点,求证:
16.如图所示,D是△ABC的边BC上的点,且CD=AB,∠ADB=∠BAD,AE 是△ABD的中线.求证:AC=2AE.
17.如图所示,在△ABC中,AB=AC,AD 是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,给出下列结论:①DE=DF;②AD上任意一点到AB,AC的距离相等;③∠BDE=∠CDF;④BD=CD,AD⊥BC.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
18.如图所示,在△ABC中,AB=AC,D是BC边上的中点,连结AD,BE平分∠ABC交AC于点E,过点 E作EF∥BC交AB 于点 F.
(1)若∠C=36°,求∠BAD的度数.
(2)求证:FB=FE.
19.在△ABC中,AC=BC,∠ACB=120°,D为AB 边的中点,∠EDF=60°,DE,DF分别交AC,BC于点E,F.
(1)如图1所示,若EF∥AB,求证:DE=DF.
(2)如图2所示,若EF与AB 不平行,则第(1)题的结论是否成立 请说明理由.
2.3 等腰三角形的性质定理(2)
1. D 2. A 3. A 4. C 5.40° 6.4 7.15°
8.∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵BD=BE,∴∠BDE=∠BED=75°.
∵AB=AC,AD是BC边上的中线,∴∠ADB=90°.
∴∠ADE=∠ADB-∠BDE=15°.
9.△ABE≌△ACE,△EBD≌△ECD,△ABD≌△ACD.以△ABE≌△ACE 为例,证明如下:
∵AD平分∠BAC,∴∠BAE=∠CAE.在△ABE 和△ACE中, ∴△ABE≌△ACE(SAS).
10. B 11. D 12. C 13.65° 14.70°
15.(1)∵∠AFD=155°,∴∠DFC=25°.
∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°.
∵AB=BC,∴∠A=∠C=65°.
∴∠B=50°,∠BDE=40°.
(2)连结BF.∵AB=BC,且 F是AC 的中点,
∴∠CFD+∠BFD=90°.
∵∠CBF+∠BFD=90°,
∴∠CFD=∠CBF.∴∠CFD= ∠ABC.
16.如答图所示,延长 AE到点 F,使 EF=AE,连结 DF.
∵AE是△ABD的中线,∴BE=DE.
在△ABE和△FDE中,
∴△ABE≌△FDE(SAS).
∴AB=FD,∠BAE=∠DFE.
∵∠ADB 是△ADC的外角,
∴∠DAC+∠ACD=∠ADB.
∵∠ADB=∠BAD=∠BAE+∠DAE,∠BAE=∠DFE,∴∠DFE+∠DAE=∠DAC+∠ACD.
∴∠ADF=∠ADC. ∵AB=DC,∴DF=DC.
在△ADF 和△ADC中,
∴△ADF≌△ADC(SAS).∴AF=AC.
∵AF=AE+EF,AE=EF,∴AC=2AE.
17. D
18.(1)∵AB=AC,∴∠C=∠ABC.
∵∠C=36°,∴∠ABC=36°.
∵BD=CD,AB=AC,∴AD⊥BC.
∴∠ADB=90°.∴∠BAD=90°-36°=54°.
(2)∵BE平分∠ABC,
∵EF∥BC,∴∠FEB=∠CBE.
∴∠FBE=∠FEB.∴FB=FE.
19.(1)∵在△ABC中,AC=BC,∠ACB=120°,
∴∠A=∠B=30°.∵EF∥AB,
∴∠FEC=∠A=30°,∠EFC=∠B=30°.
∴CE=CF.
∵D是等腰三角形ABC 的边AB 的中点,
∴CD是角平分线,即∠DCE=∠DCF.
在△DCE 和△DCF中, ∴△DCE≌△DCF(SAS),∴DE=DF.
(2)如答图所示,过点 D 作 DM⊥AC 交AC 于点M,再作 DN⊥BC交BC 于点 N.
由(1)可知 DM=DN.∠MDN=180°--∠ADM-∠BDN= 60°,∠EDF = 60°,∴∠EDM= 60°-∠EDN,∠FDN = 60° - ∠EDN. ∴∠EDM =∠FDN.又∵∠DME=∠DNF=90°,DM=DN,∴△DEM≌△DFN(ASA).∴DE=DF.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
