2.3 等腰三角形的性质定理(1) 同步练习(含答案)
文档属性
| 名称 | 2.3 等腰三角形的性质定理(1) 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 347.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 12:23:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.3 等腰三角形的性质定理(1)
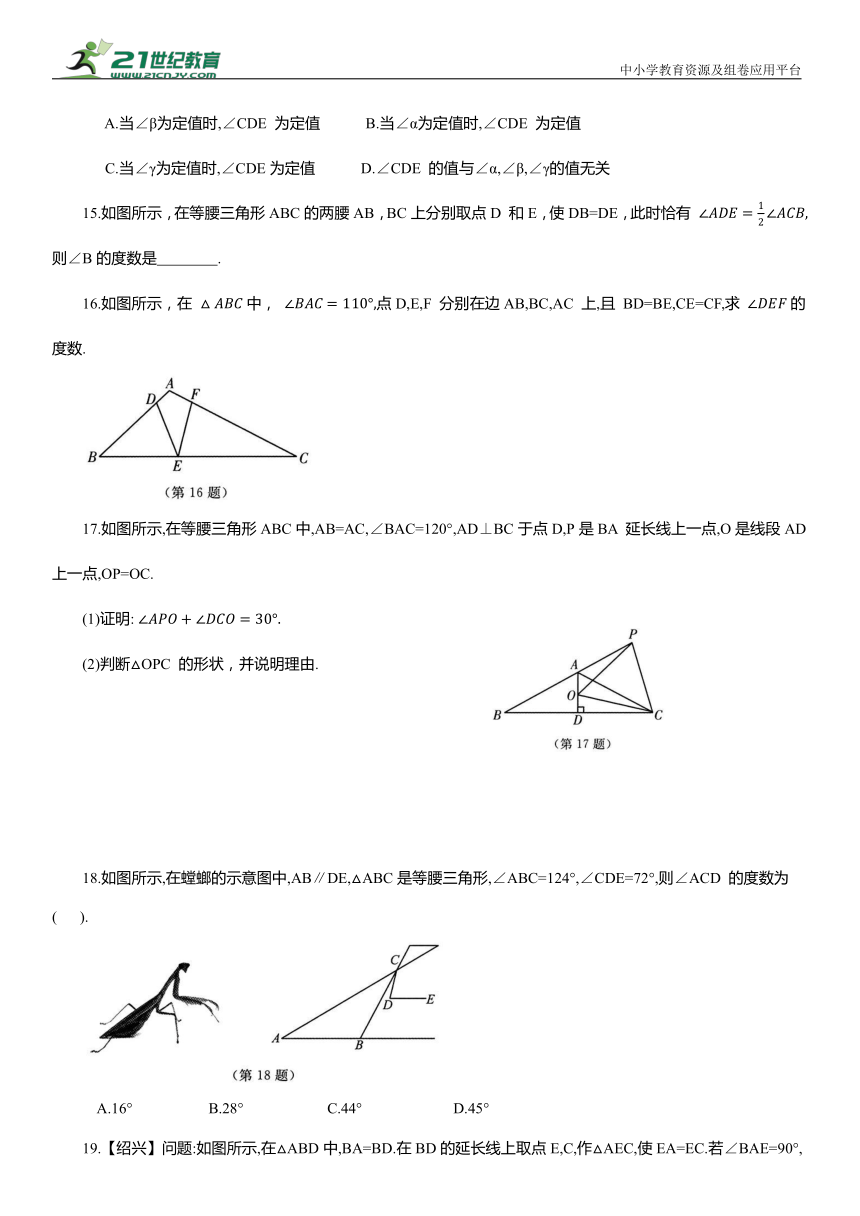
1.如图所示,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( ).
A.30° B.40° C.45° D.60°
2.如图所示,在△ABC中,AC=BC,点D在BC的延长线上,AE∥BD,点E,D在AC同侧,若∠CAE=118°,则∠B的大小为( ).
A.31° B.32° C.59° D.62°
3.若等腰三角形一个角为50°,则这个等腰三角形的顶角可能为( ).
A.50° B.65° C.80° D.50°或80°
4.如图所示,在△ABC中,AB=AC,∠ABC,∠BAC的平分线相交于点 D.若∠ADB=130°,则∠BAC的度数为( ).
A.80° B.50° C.40° D.20°
5.如图所示,已知在等腰三角形ABC中,AB=AC.若以点 B 为圆心,BC长为半径画弧,交AC于点E,则下列结论中,一定正确的是( ).
A. AE=EC B. AE=BE
C.∠EBC=∠BAC D.∠EBC=∠ABE
6.如图所示,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD= .
7.如图所示,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC=105°,∠B=40°,则∠CAE = .
8.如图所示,直线l ∥l ,点A在直线l 上,点 B在直线l 上,AB=BC,∠C=30°,∠1=80°,则∠2= .
9.如图所示,点D,E在△ABC的边BC上,AB=AC,AD=AE,在图中找出一条与BE相等的线段,并说明理由.
10.如图所示,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连结AF.求证:AF平分∠BAC.
11.如图所示,AB=AC=AD,若∠BAD=80°,则∠BCD的度数为( ).
A.80° B.100°
C.140° D.160°
12.如图所示,在△ABC中,∠C=32°,∠CAB,∠ABC的外角平分线分别交对边的延长线于D,E两点,且AC=AD,则∠E的度数为( ).
A.10° B.16° C.20° D.24°
13.如图所示,在△ABC,△ADE中,C,D两点分别在AE,AB上,BC与DE 相交于点F.若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数是( ).
A.114° B.123° C.132° D.147°
14.如图所示,D,E分别为△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( ).
A.当∠β为定值时,∠CDE 为定值 B.当∠α为定值时,∠CDE 为定值
C.当∠γ为定值时,∠CDE为定值 D.∠CDE 的值与∠α,∠β,∠γ的值无关
15.如图所示,在等腰三角形ABC的两腰AB,BC上分别取点D 和E,使DB=DE,此时恰有 则∠B的度数是 .
16.如图所示,在 中, 点D,E,F 分别在边AB,BC,AC 上,且 BD=BE,CE=CF,求 的度数.
17.如图所示,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,P是BA 延长线上一点,O是线段AD 上一点,OP=OC.
(1)证明:
(2)判断△OPC 的形状,并说明理由.
18.如图所示,在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD 的度数为( ).
A.16° B.28° C.44° D.45°
19.【绍兴】问题:如图所示,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:
(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 请说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“ 其余条件不变,求∠DAC的度数.
20.如图所示,在△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且∠ADE=∠AED,连结DE.
(1)如图1所示,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数.
(2)如图2所示,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数.
(3)当点 D在直线BC上(不与点 B,C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
2.3 等腰三角形的性质定理(1)
1. B 2. A 3. D 4. D 5. C 6.110° 7.35°8.40°
9. BE=CD.理由如下:∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED.
在△ABE与△ACD中, ∴△ABE≌△ACD(AAS).∴BE=CD.
10.∵AB=AC,∴∠EBC=∠DCB.
∵CE⊥AB,BD⊥AC,∴∠BEC=∠CDB=90°.
在△BCE和△CBD中,∴
∴△BCE≌△CBD(AAS).
∴∠ECB=∠DBC,BE=CD.
∴∠ABC--∠DBC=∠ACB-∠ECB,即∠ABF=∠ACF;AB-BE=AC--CD,即AE=AD.在△BEF和△CDF中,
∴△BEF≌△CDF(ASA).∴EF=DF.
在△AEF和△ADF中,∵
∴△AEF≌△ADF(SSS).
∴∠FAE=∠FAD,即 AF平分∠BAC.
11. C 12. A 13. B 14. B 15.20°
16.设∠B=x,∠C=y.
在△BDE中,
同理,在△CEF 中, ∵ CE = CF,∴∠CEF =
∵∠BED+∠DEF+∠CEF=180°,∴∠DEF=180° - ( ∠BED + ∠CEF) = 180° -
∵∠BAC=110°,∴x+y=180°-110°=70°.
∴∠DEF=35°.
17.(1)连结OB.∵AB=AC,AD⊥BC,∴∠ABD=∠ACD,∠ADB=∠ADC.
在△ABD 和△ACD中,∵
∴△ABD≌△ACD(AAS).
∴OB=OC,∠ABC=90°-∠BAD=30°.
∵OP=OC,∴OB=OC=OP.
∴∠APO=∠ABO,∠DCO=∠DBO.
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°.
(2)△OPC为等边三角形.理由如下:
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°.
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°.
∴∠POC=60°.由(1)知OC=OP,
∴∠OPC=∠OCP=60°.
∴△OPC是等边三角形.
18. C
19.(1)∠DAC的度数不会改变.理由如下:
∵EA=EC,∴∠EAC=∠C①.
∵BA=BD,∴∠BAD=∠BDA.
由①②得,∠DAC=∠DAE+∠CAE= 45°-∠C+∠C=45°.
(2)设∠ABC=m°,则
20.(1)∵∠B=∠C=30°,∴∠BAC=120°.
∵∠BAD=70°,∴∠DAE=50°.
∴∠ADE=∠AED=65°.
∴∠CDE=∠AED-∠C=65°-30°=35°.
(2)∵∠ACB=70°,∠CDE=15°,∴∠E=70°--15°=55°.∴∠ADE=∠AED=55°.∴∠ADC=40°.∵∠ABC=∠ADB+∠DAB=70°,∴∠BAD=30°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β.
①如答图1所示,当点 D 在点 B 的左侧时,∠ADC
两式相减,得22α-β=0,∴2α=β.
②如答图2所示,当点 D 在线段 BC 上时,∠ADC
两式相减,得α=β-α,∴2α=β.
③如答图3 所示,当点 D 在点 C右侧时,∠ADC=
两式相减,得2α-β=0,∴2α=β.
综上所述, ∠BAD 与 ∠CDE 的 数 量 关 系 是2∠CDE=∠BAD.
2.3 等腰三角形的性质定理(1)
1.如图所示,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( ).
A.30° B.40° C.45° D.60°
2.如图所示,在△ABC中,AC=BC,点D在BC的延长线上,AE∥BD,点E,D在AC同侧,若∠CAE=118°,则∠B的大小为( ).
A.31° B.32° C.59° D.62°
3.若等腰三角形一个角为50°,则这个等腰三角形的顶角可能为( ).
A.50° B.65° C.80° D.50°或80°
4.如图所示,在△ABC中,AB=AC,∠ABC,∠BAC的平分线相交于点 D.若∠ADB=130°,则∠BAC的度数为( ).
A.80° B.50° C.40° D.20°
5.如图所示,已知在等腰三角形ABC中,AB=AC.若以点 B 为圆心,BC长为半径画弧,交AC于点E,则下列结论中,一定正确的是( ).
A. AE=EC B. AE=BE
C.∠EBC=∠BAC D.∠EBC=∠ABE
6.如图所示,在△ABC中,∠C=40°,CA=CB,则△ABC的外角∠ABD= .
7.如图所示,在△ABC中,AD=AE,BD=EC,∠ADB=∠AEC=105°,∠B=40°,则∠CAE = .
8.如图所示,直线l ∥l ,点A在直线l 上,点 B在直线l 上,AB=BC,∠C=30°,∠1=80°,则∠2= .
9.如图所示,点D,E在△ABC的边BC上,AB=AC,AD=AE,在图中找出一条与BE相等的线段,并说明理由.
10.如图所示,在△ABC中,AB=AC,BD⊥AC于点D,CE⊥AB于点E,BD,CE交于点F,连结AF.求证:AF平分∠BAC.
11.如图所示,AB=AC=AD,若∠BAD=80°,则∠BCD的度数为( ).
A.80° B.100°
C.140° D.160°
12.如图所示,在△ABC中,∠C=32°,∠CAB,∠ABC的外角平分线分别交对边的延长线于D,E两点,且AC=AD,则∠E的度数为( ).
A.10° B.16° C.20° D.24°
13.如图所示,在△ABC,△ADE中,C,D两点分别在AE,AB上,BC与DE 相交于点F.若BD=CD=CE,∠ADC+∠ACD=114°,则∠DFC的度数是( ).
A.114° B.123° C.132° D.147°
14.如图所示,D,E分别为△ABC的边BC,AC上的点,若AB=AC,AD=AE,则( ).
A.当∠β为定值时,∠CDE 为定值 B.当∠α为定值时,∠CDE 为定值
C.当∠γ为定值时,∠CDE为定值 D.∠CDE 的值与∠α,∠β,∠γ的值无关
15.如图所示,在等腰三角形ABC的两腰AB,BC上分别取点D 和E,使DB=DE,此时恰有 则∠B的度数是 .
16.如图所示,在 中, 点D,E,F 分别在边AB,BC,AC 上,且 BD=BE,CE=CF,求 的度数.
17.如图所示,在等腰三角形ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,P是BA 延长线上一点,O是线段AD 上一点,OP=OC.
(1)证明:
(2)判断△OPC 的形状,并说明理由.
18.如图所示,在螳螂的示意图中,AB∥DE,△ABC是等腰三角形,∠ABC=124°,∠CDE=72°,则∠ACD 的度数为( ).
A.16° B.28° C.44° D.45°
19.【绍兴】问题:如图所示,在△ABD中,BA=BD.在BD的延长线上取点E,C,作△AEC,使EA=EC.若∠BAE=90°,∠B=45°,求∠DAC的度数.
答案:∠DAC=45°.
思考:
(1)如果把以上“问题”中的条件“∠B=45°”去掉,其余条件不变,那么∠DAC的度数会改变吗 请说明理由.
(2)如果把以上“问题”中的条件“∠B=45°”去掉,再将“∠BAE=90°”改为“ 其余条件不变,求∠DAC的度数.
20.如图所示,在△ABC中,∠ABC=∠ACB,点D在BC所在的直线上,点E在射线AC上,且∠ADE=∠AED,连结DE.
(1)如图1所示,若∠B=∠C=30°,∠BAD=70°,求∠CDE的度数.
(2)如图2所示,若∠ABC=∠ACB=70°,∠CDE=15°,求∠BAD的度数.
(3)当点 D在直线BC上(不与点 B,C重合)运动时,试探究∠BAD与∠CDE的数量关系,并说明理由.
2.3 等腰三角形的性质定理(1)
1. B 2. A 3. D 4. D 5. C 6.110° 7.35°8.40°
9. BE=CD.理由如下:∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED.
在△ABE与△ACD中, ∴△ABE≌△ACD(AAS).∴BE=CD.
10.∵AB=AC,∴∠EBC=∠DCB.
∵CE⊥AB,BD⊥AC,∴∠BEC=∠CDB=90°.
在△BCE和△CBD中,∴
∴△BCE≌△CBD(AAS).
∴∠ECB=∠DBC,BE=CD.
∴∠ABC--∠DBC=∠ACB-∠ECB,即∠ABF=∠ACF;AB-BE=AC--CD,即AE=AD.在△BEF和△CDF中,
∴△BEF≌△CDF(ASA).∴EF=DF.
在△AEF和△ADF中,∵
∴△AEF≌△ADF(SSS).
∴∠FAE=∠FAD,即 AF平分∠BAC.
11. C 12. A 13. B 14. B 15.20°
16.设∠B=x,∠C=y.
在△BDE中,
同理,在△CEF 中, ∵ CE = CF,∴∠CEF =
∵∠BED+∠DEF+∠CEF=180°,∴∠DEF=180° - ( ∠BED + ∠CEF) = 180° -
∵∠BAC=110°,∴x+y=180°-110°=70°.
∴∠DEF=35°.
17.(1)连结OB.∵AB=AC,AD⊥BC,∴∠ABD=∠ACD,∠ADB=∠ADC.
在△ABD 和△ACD中,∵
∴△ABD≌△ACD(AAS).
∴OB=OC,∠ABC=90°-∠BAD=30°.
∵OP=OC,∴OB=OC=OP.
∴∠APO=∠ABO,∠DCO=∠DBO.
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°.
(2)△OPC为等边三角形.理由如下:
∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°.
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°.
∴∠POC=60°.由(1)知OC=OP,
∴∠OPC=∠OCP=60°.
∴△OPC是等边三角形.
18. C
19.(1)∠DAC的度数不会改变.理由如下:
∵EA=EC,∴∠EAC=∠C①.
∵BA=BD,∴∠BAD=∠BDA.
由①②得,∠DAC=∠DAE+∠CAE= 45°-∠C+∠C=45°.
(2)设∠ABC=m°,则
20.(1)∵∠B=∠C=30°,∴∠BAC=120°.
∵∠BAD=70°,∴∠DAE=50°.
∴∠ADE=∠AED=65°.
∴∠CDE=∠AED-∠C=65°-30°=35°.
(2)∵∠ACB=70°,∠CDE=15°,∴∠E=70°--15°=55°.∴∠ADE=∠AED=55°.∴∠ADC=40°.∵∠ABC=∠ADB+∠DAB=70°,∴∠BAD=30°.
(3)设∠ABC=∠ACB=y°,∠ADE=∠AED=x°,∠CDE=α,∠BAD=β.
①如答图1所示,当点 D 在点 B 的左侧时,∠ADC
两式相减,得22α-β=0,∴2α=β.
②如答图2所示,当点 D 在线段 BC 上时,∠ADC
两式相减,得α=β-α,∴2α=β.
③如答图3 所示,当点 D 在点 C右侧时,∠ADC=
两式相减,得2α-β=0,∴2α=β.
综上所述, ∠BAD 与 ∠CDE 的 数 量 关 系 是2∠CDE=∠BAD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
