1.5 三角形全等的判定(3)同步练习(含答案)
文档属性
| 名称 | 1.5 三角形全等的判定(3)同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 298.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
1.5 三角形全等的判定(3)
1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),将其中的一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃,应该带( ).
A.第1块 B.第2块 C.第3块 D.第4块
2.如图所示,已知∠A=∠D,∠B=∠DEF,AB=DE.若BF=6,EC=1,则BC的长为( ).
A.4 B.3.5 C.3 D.2.5
3.如图所示,点A,B,C,D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( ).
A.3对 B.4对 C.5对 D.6对
4.如图所示,∠1=∠2,∠3=∠4,且AB=6,则CD= .
5.如图所示,∠BAC=∠ABD,BD,AC交于点O,要使OC=OD,还需添加一个条件
6.【南充】如图所示,点C在线段BD 上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
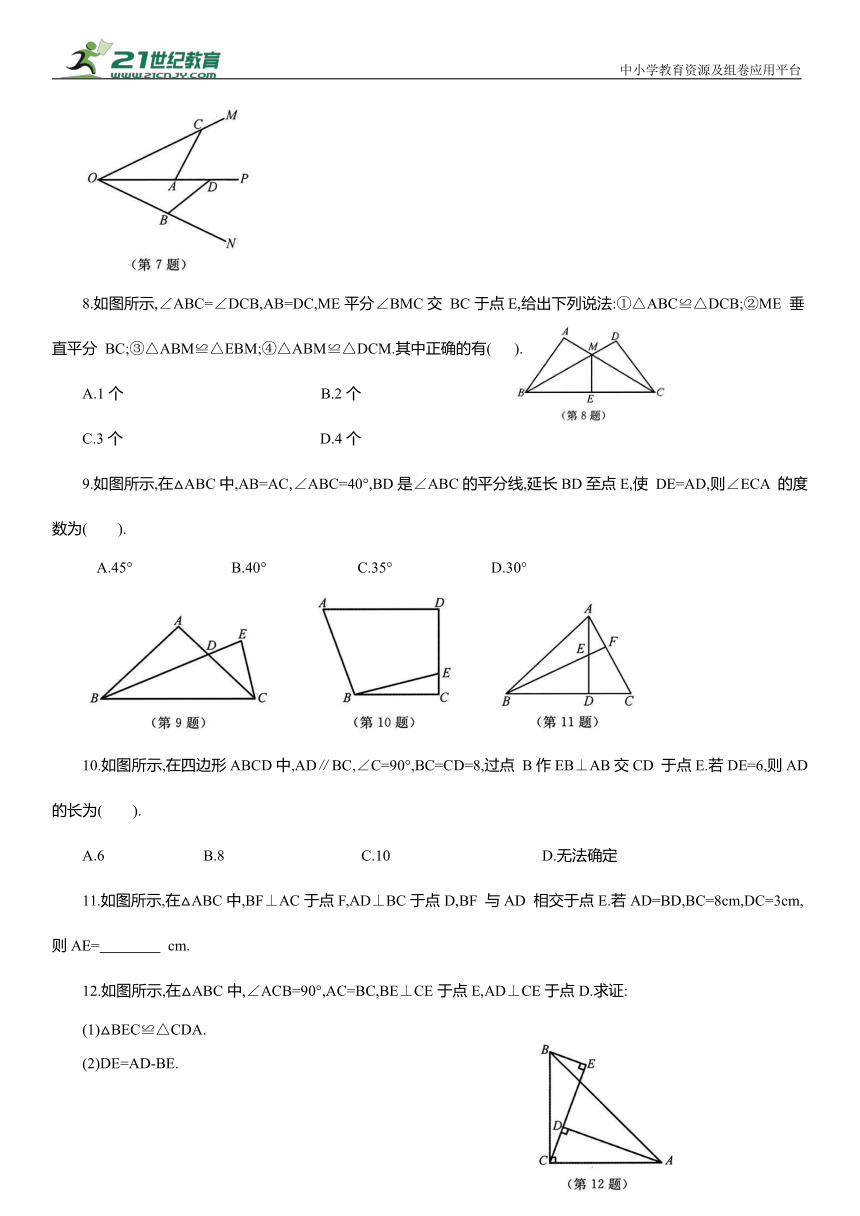
7.如图所示,OP平分∠MON,点A,B分别在OP,ON上,且OA=OB,点C,D分别在OM,OP上,且∠CAP=∠DBN.求证:AC=BD.
8.如图所示,∠ABC=∠DCB,AB=DC,ME平分∠BMC交 BC于点E,给出下列说法:①△ABC≌△DCB;②ME 垂直平分 BC;③△ABM≌△EBM;④△ABM≌△DCM.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
9.如图所示,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使 DE=AD,则∠ECA 的度数为( ).
A.45° B.40° C.35° D.30°
10.如图所示,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点 B作EB⊥AB交CD 于点E.若DE=6,则AD的长为( ).
A.6 B.8 C.10 D.无法确定
11.如图所示,在△ABC中,BF⊥AC于点F,AD⊥BC于点D,BF 与AD 相交于点E.若AD=BD,BC=8cm,DC=3cm,则AE= cm.
12.如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:
(1)△BEC≌△CDA.
(2)DE=AD-BE.
13.如图所示,已知AB=AC,点 D,E分别在线段AB,AC上,BE与CD 相交于点O,添加下列条件后仍不能判定△ABE≌△ACD 的是( ).
A.∠B=∠C B. AE=AD
C. BD=CE D. BE=CD
14.【苏州】如图所示,∠A=∠B,AE=BE,点 D 在AC 边上,∠1=∠2,AE 和BD 相交于点O.求证:△AEC≌△BED.
15.在解决线段数量关系问题的过程中,如果条件中有角平分线,那么通常可以采用构造全等三角形的思路,如:在图1中,已知C是∠MON的平分线OP 上一点,点A 在OM上,此时,在ON上截取OB=OA,连结BC,根据三角形全等判定(SAS),容易构造出全等三角形△OBC 和△OAC.参考上面的方法,解答下列问题.
如图2所示,在非等边三角形ABC中,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,且AD,CE交于点 F.求证:AC=AE+CD.
1.5 三角形全等的判定(3)
1. B 2. B 3. D 4.6 5.∠DAB=∠CBA(答案不唯一)
6.∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°.
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°.
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA).∴AB=CD.
7.∵OP 平分∠MON,∴∠COA=∠DOB.
∵∠CAP=∠DBN,∴∠CAO=∠DBO.
在△COA 和△DOB中, ∴△COA≌△DOB(ASA).∴AC=BD.
8. C 9. B 10. C 11.2
12.(1)∵BE⊥CE于点E,AD⊥CE于点D,∴∠BEC=∠CDA=90°.
∴∠BCE+∠CBE=90°.
∵∠BCE+∠ACD=90°,∴∠CBE=∠ACD.
∴∠BCE=∠CAD.
在△BEC和△CDA中, ∴△BEC≌△CDA(ASA).
(2)∵△BEC≌△CDA.∴CE=AD,BE=CD.∴DE=CE-CD=AD-BE.
13. D
14.∵AE和BD 相交于点O,∴∠AOD=∠BOE.在△AOD 和△BOE中,∵∠A=∠B,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO.∴∠AEC=∠BED.
在△AEC和△BED中, ∴△AEC≌△BED(ASA).
15.如答图所示,在AC上截取AG=AE,连结 FG.
∵AD是∠BAC 的平分线,CE是∠BCA的平分线,
∴∠1=∠2,3=∠4.
在△AEF 和△AGF中,
∴△AEF≌△AGF(SAS).
∴∠AFE=∠AFG.
∵∠B=60°,∴∠BAC+∠ACB=120°.
∵∠AFE=∠2+∠3,
∴∠AFE=∠CFD=∠AFG=60°.
∴∠CFG=180°-∠CFD--∠AFG=60°.
∴∠CFD=∠CFG.
在△CFG和△CFD中, ∴△CFG≌△CFD(ASA).∴CG=CD.
∴AC=AG+CG=AE+CD.
1.5 三角形全等的判定(3)
1.小明不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标有1,2,3,4的四块),将其中的一块带去玻璃店,就能配一块与原来一样大小的三角形玻璃,应该带( ).
A.第1块 B.第2块 C.第3块 D.第4块
2.如图所示,已知∠A=∠D,∠B=∠DEF,AB=DE.若BF=6,EC=1,则BC的长为( ).
A.4 B.3.5 C.3 D.2.5
3.如图所示,点A,B,C,D在同一条直线上,∠EAD=∠FAD,∠EDA=∠FDA,则图中共有全等三角形( ).
A.3对 B.4对 C.5对 D.6对
4.如图所示,∠1=∠2,∠3=∠4,且AB=6,则CD= .
5.如图所示,∠BAC=∠ABD,BD,AC交于点O,要使OC=OD,还需添加一个条件
6.【南充】如图所示,点C在线段BD 上,且AB⊥BD,DE⊥BD,AC⊥CE,BC=DE.求证:AB=CD.
7.如图所示,OP平分∠MON,点A,B分别在OP,ON上,且OA=OB,点C,D分别在OM,OP上,且∠CAP=∠DBN.求证:AC=BD.
8.如图所示,∠ABC=∠DCB,AB=DC,ME平分∠BMC交 BC于点E,给出下列说法:①△ABC≌△DCB;②ME 垂直平分 BC;③△ABM≌△EBM;④△ABM≌△DCM.其中正确的有( ).
A.1个 B.2个
C.3个 D.4个
9.如图所示,在△ABC中,AB=AC,∠ABC=40°,BD是∠ABC的平分线,延长BD至点E,使 DE=AD,则∠ECA 的度数为( ).
A.45° B.40° C.35° D.30°
10.如图所示,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点 B作EB⊥AB交CD 于点E.若DE=6,则AD的长为( ).
A.6 B.8 C.10 D.无法确定
11.如图所示,在△ABC中,BF⊥AC于点F,AD⊥BC于点D,BF 与AD 相交于点E.若AD=BD,BC=8cm,DC=3cm,则AE= cm.
12.如图所示,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:
(1)△BEC≌△CDA.
(2)DE=AD-BE.
13.如图所示,已知AB=AC,点 D,E分别在线段AB,AC上,BE与CD 相交于点O,添加下列条件后仍不能判定△ABE≌△ACD 的是( ).
A.∠B=∠C B. AE=AD
C. BD=CE D. BE=CD
14.【苏州】如图所示,∠A=∠B,AE=BE,点 D 在AC 边上,∠1=∠2,AE 和BD 相交于点O.求证:△AEC≌△BED.
15.在解决线段数量关系问题的过程中,如果条件中有角平分线,那么通常可以采用构造全等三角形的思路,如:在图1中,已知C是∠MON的平分线OP 上一点,点A 在OM上,此时,在ON上截取OB=OA,连结BC,根据三角形全等判定(SAS),容易构造出全等三角形△OBC 和△OAC.参考上面的方法,解答下列问题.
如图2所示,在非等边三角形ABC中,∠B=60°,AD,CE分别是∠BAC,∠BCA的平分线,且AD,CE交于点 F.求证:AC=AE+CD.
1.5 三角形全等的判定(3)
1. B 2. B 3. D 4.6 5.∠DAB=∠CBA(答案不唯一)
6.∵AB⊥BD,ED⊥BD,AC⊥CE,
∴∠ACE=∠ABC=∠CDE=90°.
∴∠ACB+∠ECD=90°,∠ECD+∠CED=90°.
∴∠ACB=∠CED.
在△ABC和△CDE中,
∴△ABC≌△CDE(ASA).∴AB=CD.
7.∵OP 平分∠MON,∴∠COA=∠DOB.
∵∠CAP=∠DBN,∴∠CAO=∠DBO.
在△COA 和△DOB中, ∴△COA≌△DOB(ASA).∴AC=BD.
8. C 9. B 10. C 11.2
12.(1)∵BE⊥CE于点E,AD⊥CE于点D,∴∠BEC=∠CDA=90°.
∴∠BCE+∠CBE=90°.
∵∠BCE+∠ACD=90°,∴∠CBE=∠ACD.
∴∠BCE=∠CAD.
在△BEC和△CDA中, ∴△BEC≌△CDA(ASA).
(2)∵△BEC≌△CDA.∴CE=AD,BE=CD.∴DE=CE-CD=AD-BE.
13. D
14.∵AE和BD 相交于点O,∴∠AOD=∠BOE.在△AOD 和△BOE中,∵∠A=∠B,∴∠BEO=∠2.又∵∠1=∠2,∴∠1=∠BEO.∴∠AEC=∠BED.
在△AEC和△BED中, ∴△AEC≌△BED(ASA).
15.如答图所示,在AC上截取AG=AE,连结 FG.
∵AD是∠BAC 的平分线,CE是∠BCA的平分线,
∴∠1=∠2,3=∠4.
在△AEF 和△AGF中,
∴△AEF≌△AGF(SAS).
∴∠AFE=∠AFG.
∵∠B=60°,∴∠BAC+∠ACB=120°.
∵∠AFE=∠2+∠3,
∴∠AFE=∠CFD=∠AFG=60°.
∴∠CFG=180°-∠CFD--∠AFG=60°.
∴∠CFD=∠CFG.
在△CFG和△CFD中, ∴△CFG≌△CFD(ASA).∴CG=CD.
∴AC=AG+CG=AE+CD.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
