4.5第二课时 相似三角形的性质及其应用 学习任务单(无答案)2024-2025学年浙教版数学九年级上册
文档属性
| 名称 | 4.5第二课时 相似三角形的性质及其应用 学习任务单(无答案)2024-2025学年浙教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 316.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览


文档简介
学习任务单
课程基本信息
学科 初中数学 年级 九年级 学期 秋季
课题 相似三角形的性质及其应用(第二课时)
学习目标
1.掌握相似三角形的周长比和面积比与相似比的关系. 2.利用相似三角形的周长比和面积比与相似比的关系求相关图形的面积.
课前学习任务
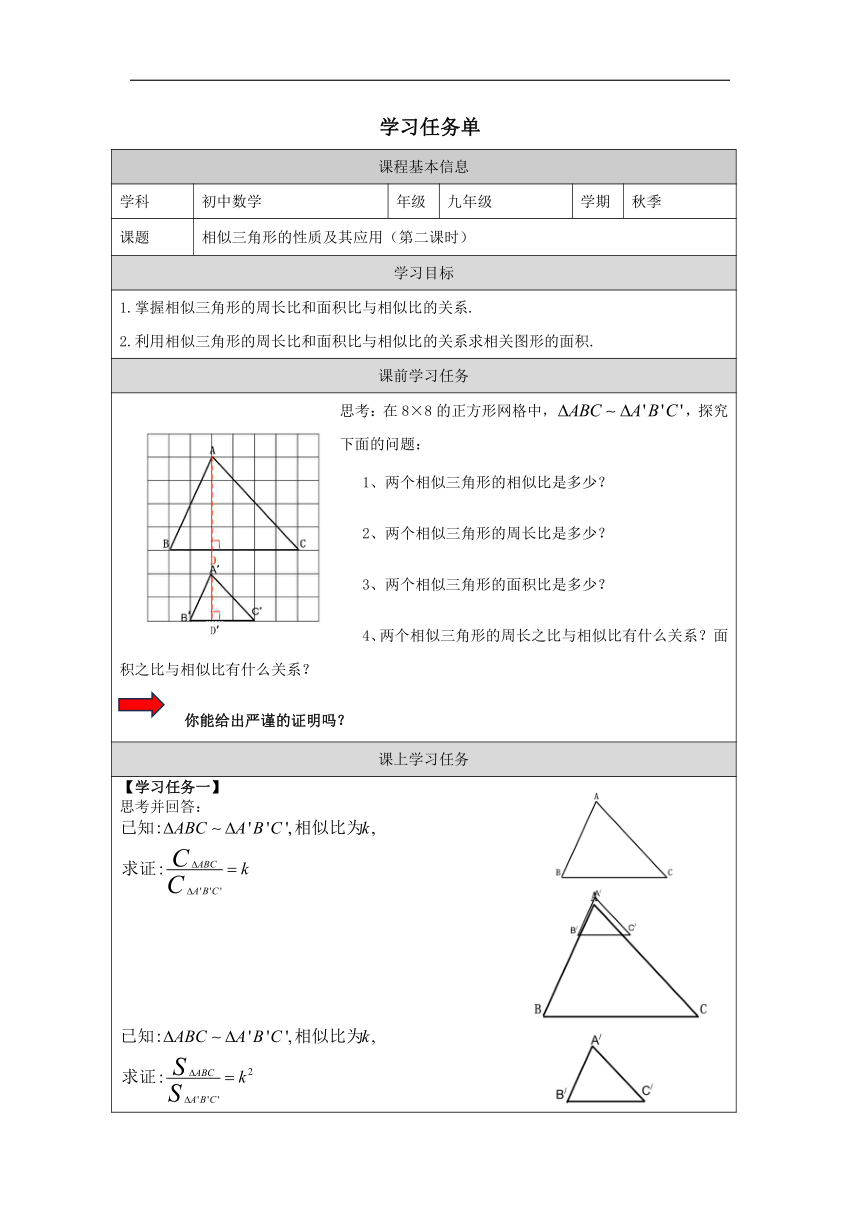
思考:在8×8的正方形网格中,,探究下面的问题: 1、两个相似三角形的相似比是多少? 2、两个相似三角形的周长比是多少? 3、两个相似三角形的面积比是多少? 4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系? 你能给出严谨的证明吗?
课上学习任务
【学习任务一】 思考并回答: (相似三角形的对应边上的高之比等于相似比) 【学习任务二】 思考并回答:由学习任务一,你能归纳出相似三角形周长和面积的性质吗?将这个命题转化成数学语言应该怎么表述呢? 【学习任务三】 思考并回答:如图,四边形ABCD中,对角线AC,BD相交于点O,AD=1,BC=4,则与的面积比等于( ) 【学习任务四】 例3 如图,是某市部分街道图,比例尺为1:100 000;请估计三条道路围成的三角形地块ABC的实际周长和面积. 例4 如图,在△ABC中,作DE//BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,问AD与AB的比应取多少? 【学习任务五】 思考并回答; 1、 2、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,DE∥BC,DF∥AC.已知,△ABC的面积为a.求DFCE的面积. 3、如图,已知△ABC,如何作一条与BC 平行的直线,把△ABC划分成两部分,使划分成的三角形和四边形的面积之比为为1:n呢? 4、在10倍的放大镜下看到的三角形与原三角形相比,哪些量被放大了10倍?其余的量如何变化? 周长 面积 【学习任务六】 完成图中的填空.
课程基本信息
学科 初中数学 年级 九年级 学期 秋季
课题 相似三角形的性质及其应用(第二课时)
学习目标
1.掌握相似三角形的周长比和面积比与相似比的关系. 2.利用相似三角形的周长比和面积比与相似比的关系求相关图形的面积.
课前学习任务
思考:在8×8的正方形网格中,,探究下面的问题: 1、两个相似三角形的相似比是多少? 2、两个相似三角形的周长比是多少? 3、两个相似三角形的面积比是多少? 4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系? 你能给出严谨的证明吗?
课上学习任务
【学习任务一】 思考并回答: (相似三角形的对应边上的高之比等于相似比) 【学习任务二】 思考并回答:由学习任务一,你能归纳出相似三角形周长和面积的性质吗?将这个命题转化成数学语言应该怎么表述呢? 【学习任务三】 思考并回答:如图,四边形ABCD中,对角线AC,BD相交于点O,AD=1,BC=4,则与的面积比等于( ) 【学习任务四】 例3 如图,是某市部分街道图,比例尺为1:100 000;请估计三条道路围成的三角形地块ABC的实际周长和面积. 例4 如图,在△ABC中,作DE//BC,分别交AB,AC于点D,E.若要使△ADE与四边形DBCE的面积相等,问AD与AB的比应取多少? 【学习任务五】 思考并回答; 1、 2、如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,DE∥BC,DF∥AC.已知,△ABC的面积为a.求DFCE的面积. 3、如图,已知△ABC,如何作一条与BC 平行的直线,把△ABC划分成两部分,使划分成的三角形和四边形的面积之比为为1:n呢? 4、在10倍的放大镜下看到的三角形与原三角形相比,哪些量被放大了10倍?其余的量如何变化? 周长 面积 【学习任务六】 完成图中的填空.
同课章节目录
