4.3 坐标平面内图形的轴对称和平移(1)同步练习(含答案)
文档属性
| 名称 | 4.3 坐标平面内图形的轴对称和平移(1)同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 275.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 20:11:21 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.3 坐标平面内图形的轴对称和平移(1)
1.在平面直角坐标系中,点P(1,-2)关于y轴的对称点的坐标是( ).
A.(-1,2) B.(-1,-2) C.(1,2) D.(2,-1)
2.已知点 P(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是( ).
A. a<-1
3.线段MN在平面直角坐标系中的位置如图所示,若线段M'N'与MN 关于y 轴对称,则点M 的对应点M'的坐标为( ).
A.(4,2) B.(-4,2) C.(-4,-2) D.(4,-2)
4.已知点 P(3,a)关于y轴的对称点为Q(b,2),则 ab= .
5.【达州】如图所示,点 P(--2,1)与点 Q(a,b)关于直线l:y=--1对称,则a+b= .
6.如图所示,在平面直角坐标系中,已知点A(1,0),点B(-4,0),直线l经过点A 且与x轴垂直.若点 B关于y轴的对称点是B ,点B 关于直线l的对称点是B ,则点 B 的坐标是
7.在平面直角坐标系中,已知A(1,-5),B(4,2),C(-1,0)三点.
(1)点B关于x轴的对称点B'的坐标为 ,点C关于y轴的对称点C'的坐标为
(2)求(1)中△AB'C'的面积.
8.已知在平面直角坐标系中,点A,B的坐标分别为A(-3,4),B(4,-2).
(1)求点 A,B关于 y轴对称的点的坐标.
(2)在平面直角坐标系中分别作出点 A,B关于x轴的对称点M,N,顺次连结AM,BM,BN,AN,求四边形 AMBN 的面积.
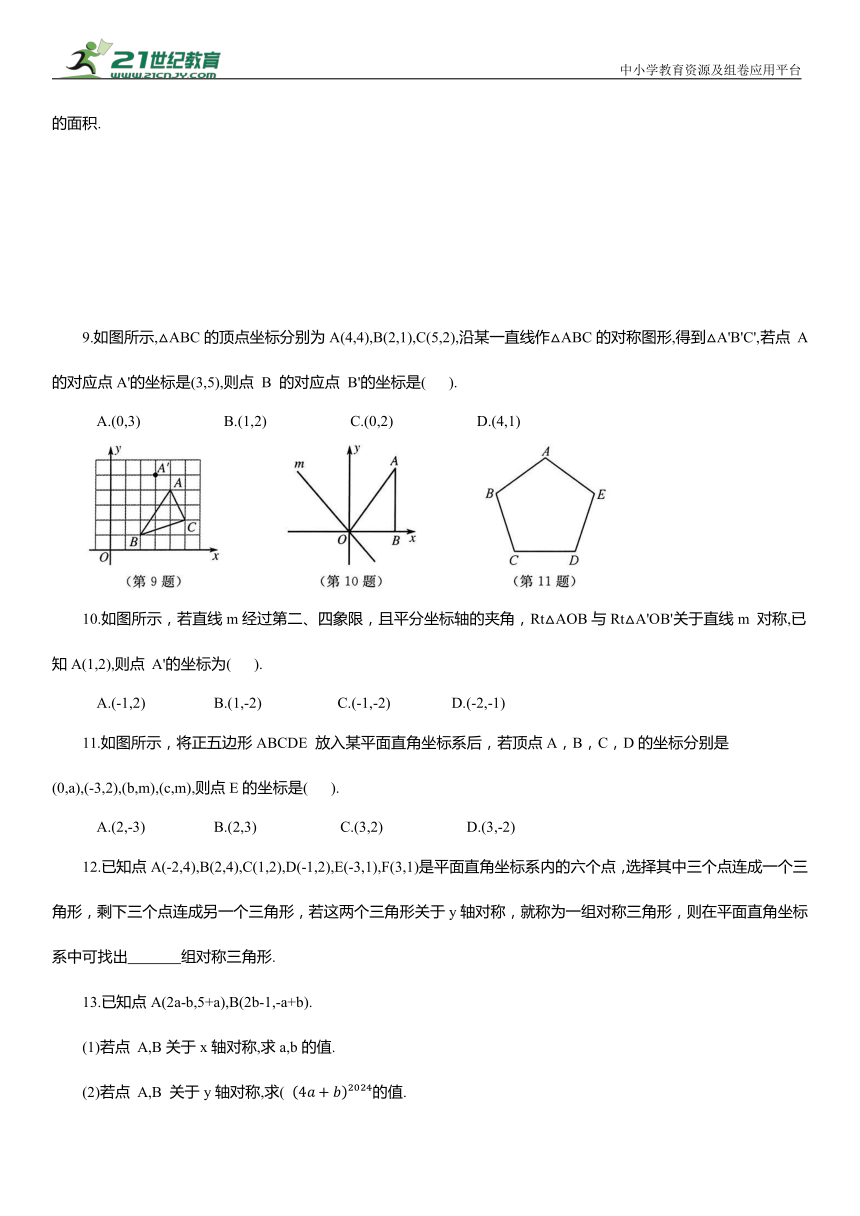
9.如图所示,△ABC的顶点坐标分别为A(4,4),B(2,1),C(5,2),沿某一直线作△ABC的对称图形,得到△A'B'C',若点 A 的对应点A'的坐标是(3,5),则点 B 的对应点 B'的坐标是( ).
A.(0,3) B.(1,2) C.(0,2) D.(4,1)
10.如图所示,若直线m经过第二、四象限,且平分坐标轴的夹角,Rt△AOB与Rt△A'OB'关于直线m 对称,已知A(1,2),则点 A'的坐标为( ).
A.(-1,2) B.(1,-2) C.(-1,-2) D.(-2,-1)
11.如图所示,将正五边形ABCDE 放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( ).
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
12.已知点A(-2,4),B(2,4),C(1,2),D(-1,2),E(-3,1),F(3,1)是平面直角坐标系内的六个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形,若这两个三角形关于y轴对称,就称为一组对称三角形,则在平面直角坐标系中可找出 组对称三角形.
13.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点 A,B关于x轴对称,求a,b的值.
(2)若点 A,B 关于y轴对称,求( 的值.
14.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A B C ,△A B C 关于直线l的对称图形是△A B C ,写出△A B C 的三个顶点的坐标.
(2)如果点 P 的坐标是(-a,0),其中a>0,点 P 关于y轴的对称点是P ,点 P 关于直线l的对称点是P ,求 PP 的长.
15.如图所示,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( ).
A.点A B.点 B
C.点 C D.点 D
16.在平面直角坐标系中,点A 的坐标是(2,-3),作点 A 关于x轴的对称点,得到点A',再作点 A'关于y 轴的对称点,得到点 A",则点 A"的坐标是 .
17.如图所示,在平面直角坐标系中,直线l:y=x是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线l的对称点A'的坐标为(2,0),请在图中分别标明B(5,3),C(--2,5)关于直线l的对称点 B',C'的位置,并写出它们的坐标:B' ,C' .
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 P(m,n)关于第一、三象限的角平分线l的对称点 P'的坐标为 .
4.3 坐标平面内图形的轴对称和平移(1)
1. B 2. B 3. D 4.-6 5.-5 6.(-2,0)
7.(1)(4,-2) (1,0)
(2)∵A(1,-5),C'(1,0),
∴AC'⊥x轴,且.
点 B'到AC'的距离为4-1=3,
∴△AB'C'的面积为
8.(1)点 A(-3,4)关于 y轴对称的点的坐标是(3,4),点 B(4,-2)关于 y轴对称的点的坐标是(-4,-2).
(2)∵点 M,N与点A,B关于x轴对称,
∴M(-3,-4),N(4,2).
∴四边形 AMBN为梯形,且AM=8,BN=4,梯形AMBN 的高为 7.∴ 四边形 AMBN 的面积为
9. A 10. D 11. C 12.4
13.(1)∵点 A,B关于x轴对称,
解得
(2)∵点 A,B关于y轴对称,
解得
14.(1)A (4,0),B (5,0),C (5,2).
(2)设 P (x,0).当0∵点 P 与P 关于y轴对称,P(-a,0),∴P (a,0).
∵点 P 与 P 关于直线l:x=3对称,
即x=6-a. ∴P (6-a,0).
∴PP =6-a-(-a)=6-a+a=6.
当a>3时,∵点 P与 P 关于y轴对称,P(-a,0),
∴P (a,0).
∵点 P 与 P 关于直线l:x=3对称,
即x=6-a.
综上可得,
15. B 16.(-2,3)
17.作图略 (3,5) (5,-2) (n,m)
4.3 坐标平面内图形的轴对称和平移(1)
1.在平面直角坐标系中,点P(1,-2)关于y轴的对称点的坐标是( ).
A.(-1,2) B.(-1,-2) C.(1,2) D.(2,-1)
2.已知点 P(a+1,2a-3)关于x轴的对称点在第一象限,则a的取值范围是( ).
A. a<-1
3.线段MN在平面直角坐标系中的位置如图所示,若线段M'N'与MN 关于y 轴对称,则点M 的对应点M'的坐标为( ).
A.(4,2) B.(-4,2) C.(-4,-2) D.(4,-2)
4.已知点 P(3,a)关于y轴的对称点为Q(b,2),则 ab= .
5.【达州】如图所示,点 P(--2,1)与点 Q(a,b)关于直线l:y=--1对称,则a+b= .
6.如图所示,在平面直角坐标系中,已知点A(1,0),点B(-4,0),直线l经过点A 且与x轴垂直.若点 B关于y轴的对称点是B ,点B 关于直线l的对称点是B ,则点 B 的坐标是
7.在平面直角坐标系中,已知A(1,-5),B(4,2),C(-1,0)三点.
(1)点B关于x轴的对称点B'的坐标为 ,点C关于y轴的对称点C'的坐标为
(2)求(1)中△AB'C'的面积.
8.已知在平面直角坐标系中,点A,B的坐标分别为A(-3,4),B(4,-2).
(1)求点 A,B关于 y轴对称的点的坐标.
(2)在平面直角坐标系中分别作出点 A,B关于x轴的对称点M,N,顺次连结AM,BM,BN,AN,求四边形 AMBN 的面积.
9.如图所示,△ABC的顶点坐标分别为A(4,4),B(2,1),C(5,2),沿某一直线作△ABC的对称图形,得到△A'B'C',若点 A 的对应点A'的坐标是(3,5),则点 B 的对应点 B'的坐标是( ).
A.(0,3) B.(1,2) C.(0,2) D.(4,1)
10.如图所示,若直线m经过第二、四象限,且平分坐标轴的夹角,Rt△AOB与Rt△A'OB'关于直线m 对称,已知A(1,2),则点 A'的坐标为( ).
A.(-1,2) B.(1,-2) C.(-1,-2) D.(-2,-1)
11.如图所示,将正五边形ABCDE 放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( ).
A.(2,-3) B.(2,3) C.(3,2) D.(3,-2)
12.已知点A(-2,4),B(2,4),C(1,2),D(-1,2),E(-3,1),F(3,1)是平面直角坐标系内的六个点,选择其中三个点连成一个三角形,剩下三个点连成另一个三角形,若这两个三角形关于y轴对称,就称为一组对称三角形,则在平面直角坐标系中可找出 组对称三角形.
13.已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点 A,B关于x轴对称,求a,b的值.
(2)若点 A,B 关于y轴对称,求( 的值.
14.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.
(1)△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A B C ,△A B C 关于直线l的对称图形是△A B C ,写出△A B C 的三个顶点的坐标.
(2)如果点 P 的坐标是(-a,0),其中a>0,点 P 关于y轴的对称点是P ,点 P 关于直线l的对称点是P ,求 PP 的长.
15.如图所示,在3×3的正方形网格中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( ).
A.点A B.点 B
C.点 C D.点 D
16.在平面直角坐标系中,点A 的坐标是(2,-3),作点 A 关于x轴的对称点,得到点A',再作点 A'关于y 轴的对称点,得到点 A",则点 A"的坐标是 .
17.如图所示,在平面直角坐标系中,直线l:y=x是第一、三象限的角平分线.
实验与探究:由图观察易知A(0,2)关于直线l的对称点A'的坐标为(2,0),请在图中分别标明B(5,3),C(--2,5)关于直线l的对称点 B',C'的位置,并写出它们的坐标:B' ,C' .
归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点 P(m,n)关于第一、三象限的角平分线l的对称点 P'的坐标为 .
4.3 坐标平面内图形的轴对称和平移(1)
1. B 2. B 3. D 4.-6 5.-5 6.(-2,0)
7.(1)(4,-2) (1,0)
(2)∵A(1,-5),C'(1,0),
∴AC'⊥x轴,且.
点 B'到AC'的距离为4-1=3,
∴△AB'C'的面积为
8.(1)点 A(-3,4)关于 y轴对称的点的坐标是(3,4),点 B(4,-2)关于 y轴对称的点的坐标是(-4,-2).
(2)∵点 M,N与点A,B关于x轴对称,
∴M(-3,-4),N(4,2).
∴四边形 AMBN为梯形,且AM=8,BN=4,梯形AMBN 的高为 7.∴ 四边形 AMBN 的面积为
9. A 10. D 11. C 12.4
13.(1)∵点 A,B关于x轴对称,
解得
(2)∵点 A,B关于y轴对称,
解得
14.(1)A (4,0),B (5,0),C (5,2).
(2)设 P (x,0).当0
∵点 P 与 P 关于直线l:x=3对称,
即x=6-a. ∴P (6-a,0).
∴PP =6-a-(-a)=6-a+a=6.
当a>3时,∵点 P与 P 关于y轴对称,P(-a,0),
∴P (a,0).
∵点 P 与 P 关于直线l:x=3对称,
即x=6-a.
综上可得,
15. B 16.(-2,3)
17.作图略 (3,5) (5,-2) (n,m)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
