4.2 平面直角坐标系(2) 同步练习(含答案)
文档属性
| 名称 | 4.2 平面直角坐标系(2) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 147.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.2 平面直角坐标系(2)
1.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( ).
A.相交,相交 B.平行,垂直相交
C.垂直相交,平行 D.平行,平行
2.若点 P(2,-4),Q(x,-4)之间的距离是3,则x的值为( ).
A.3 B.5 C. -1 D.5或-1
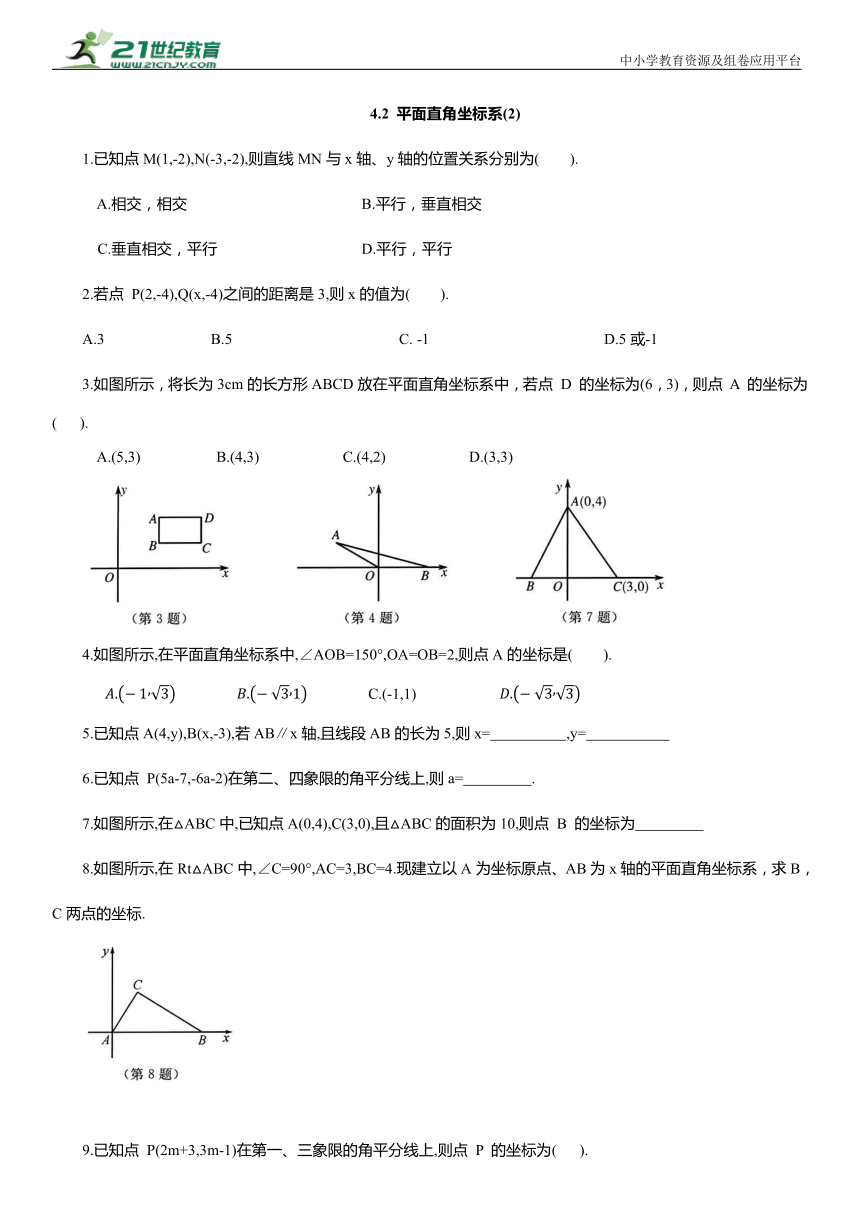
3.如图所示,将长为3cm的长方形ABCD放在平面直角坐标系中,若点 D 的坐标为(6,3),则点 A 的坐标为( ).
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
4.如图所示,在平面直角坐标系中,∠AOB=150°,OA=OB=2,则点A的坐标是( ).
C.(-1,1)
5.已知点A(4,y),B(x,-3),若AB∥x轴,且线段AB的长为5,则x= ,y=
6.已知点 P(5a-7,-6a-2)在第二、四象限的角平分线上,则a= .
7.如图所示,在△ABC中,已知点A(0,4),C(3,0),且△ABC的面积为10,则点 B 的坐标为
8.如图所示,在Rt△ABC中,∠C=90°,AC=3,BC=4.现建立以A为坐标原点、AB为x轴的平面直角坐标系,求B,C两点的坐标.
9.已知点 P(2m+3,3m-1)在第一、三象限的角平分线上,则点 P 的坐标为( ).
A.(4,4) B.(3,3) C.(11,11) D.(-11,-11)
10.在平面直角坐标系中有点 A(-2,-1),B(-4,3),C(0,0),则△ABC的面积为( ).
A.5 B.6 C.8 D.3
11.如图所示,已知△ABC为直角三角形,∠B=90°,AB⊥x轴,M为AC 中点.若点A 的坐标为(3,4),点 M 的坐标为(-1,1),则点 B 的坐标为( ).
A.(3,-4) B.(3,-3)
C.(3,-2) D.(3,-1)
12.如图所示,在平面直角坐标系中,直线l交x轴于点A(-2,0),交 y轴于点A (0,2),点 A ,A ,…在直线l上,点 B ,B ,B ,…在x轴的正半轴上.若△A OB ,△A B B ,△A B B ,…依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形A B B 的顶点B 的横坐标为 .
13.如图所示,在四边形ABCD中,AB∥CD,BC⊥AB,AD=5,CD=3,BC=4.
(1)在图中建立适当的平面直角坐标系,并写出各顶点的坐标.
(2)在(1)的基础上,分别写出线段CD和AD 中点的坐标.
14.如图所示,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使 求点 M的坐标.
15.如图所示,动点 P 从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点(1,0),第2秒运动到点(1,1),第3秒运动到点(0,1),第4秒运动到点(0,2)……则第2068秒,点 P 所在位置的坐标是 .
16.定义:在平面直角坐标系中,把从点 P 出发沿纵或横方向到达点 Q(至多拐一次弯)的路径长称为 P,Q的“实际距离”.如图所示,若 P(-1,1),Q(2,3),则 P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.如今环保低碳的共享单车已成为市民出行喜欢的交通工具,设A,B,C三个小区的坐标分别为A(3,1),B(5,-3),C(-1,-5),若点 M表示共享单车停放点,且满足M到A,B,C的“实际距离”相等,则点 M的坐标为 .
17.阅读材料,回答下列问题:
已知平面内两点M(x ,y ),N(x ,y ),则这两点间的距离可用下列公式计算:
例如:已知点 P(3,1),Q(1,-2),则这两点间的距离
特别地,如果两点M(x ,y ),N(x ,y )所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为 或
(1)已知A(1,2),B(-2,-3),试求A,B两点间的距离.
(2)已知点A,B在平行于y轴的同一条直线上,点A 的纵坐标为5,点B 的纵坐标为-1,试求A,B两点间的距离.
(3)已知△ABC的顶点坐标分别为A(0,4),B(-1,2),C(4,2),你能判定△ABC的形状吗 请说明理由.
1. B 2. D 3. D 4. B 5.9或-1 - 3 6.-97.(-2,0)
8.∵∠C=90°,AC=3,BC=4,
即点 B 的坐标为(5,0).过点C作CD⊥AB于点D,则
∴点 C的坐标为
9. C 10. A 11. C 12.2"+ -2
13.(1)本题建立平面直角坐标系答案不唯一.以直线 AB为x轴,直线 BC为y轴,点 B 为原点O 建立平面直角坐标系,如答图所示.
∵CD=3,BC=4,∴点 B(0,0),点 C(0,4),点D(-3,4).
过点 D作DE⊥AB于点E,则DE=BC=4.
∵AD=5,DE=4,∴AE= √AD -DE =3.
∴AB=AE+BE=3+3=6.∴点A(-6,0).
(2)取线段CD的中点M,线段AD的中点N.
∵C(0,4),D(-3,4),A(-6,0),
∴点 点
14.(1)∵|2a+b+1|+(a+2b-4) =0,
∴|2a+b+1|=0且
解得 即a=-2,b=3.
(2)如答图所示,过点 C作CT⊥x轴,CS⊥y轴,垂足分别为点 T,S.
∵A(-2,0),B(3,0),
∴AB=5.
∵C(-1,2),
∴CT=2,CS=1.
∴要使 则 即
∴点M的坐标为(0,5).
15.(45,43)16.(1,-2)
(2)AB=5--(-1)=6.
(3)△ABC为直角三角形.理由如下:
为直角三角形.
4.2 平面直角坐标系(2)
1.已知点M(1,-2),N(-3,-2),则直线MN与x轴、y轴的位置关系分别为( ).
A.相交,相交 B.平行,垂直相交
C.垂直相交,平行 D.平行,平行
2.若点 P(2,-4),Q(x,-4)之间的距离是3,则x的值为( ).
A.3 B.5 C. -1 D.5或-1
3.如图所示,将长为3cm的长方形ABCD放在平面直角坐标系中,若点 D 的坐标为(6,3),则点 A 的坐标为( ).
A.(5,3) B.(4,3) C.(4,2) D.(3,3)
4.如图所示,在平面直角坐标系中,∠AOB=150°,OA=OB=2,则点A的坐标是( ).
C.(-1,1)
5.已知点A(4,y),B(x,-3),若AB∥x轴,且线段AB的长为5,则x= ,y=
6.已知点 P(5a-7,-6a-2)在第二、四象限的角平分线上,则a= .
7.如图所示,在△ABC中,已知点A(0,4),C(3,0),且△ABC的面积为10,则点 B 的坐标为
8.如图所示,在Rt△ABC中,∠C=90°,AC=3,BC=4.现建立以A为坐标原点、AB为x轴的平面直角坐标系,求B,C两点的坐标.
9.已知点 P(2m+3,3m-1)在第一、三象限的角平分线上,则点 P 的坐标为( ).
A.(4,4) B.(3,3) C.(11,11) D.(-11,-11)
10.在平面直角坐标系中有点 A(-2,-1),B(-4,3),C(0,0),则△ABC的面积为( ).
A.5 B.6 C.8 D.3
11.如图所示,已知△ABC为直角三角形,∠B=90°,AB⊥x轴,M为AC 中点.若点A 的坐标为(3,4),点 M 的坐标为(-1,1),则点 B 的坐标为( ).
A.(3,-4) B.(3,-3)
C.(3,-2) D.(3,-1)
12.如图所示,在平面直角坐标系中,直线l交x轴于点A(-2,0),交 y轴于点A (0,2),点 A ,A ,…在直线l上,点 B ,B ,B ,…在x轴的正半轴上.若△A OB ,△A B B ,△A B B ,…依次均为等腰直角三角形,直角顶点都在x轴上,则第n个等腰直角三角形A B B 的顶点B 的横坐标为 .
13.如图所示,在四边形ABCD中,AB∥CD,BC⊥AB,AD=5,CD=3,BC=4.
(1)在图中建立适当的平面直角坐标系,并写出各顶点的坐标.
(2)在(1)的基础上,分别写出线段CD和AD 中点的坐标.
14.如图所示,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-
(1)求a,b的值.
(2)在y轴的正半轴上存在一点M,使 求点 M的坐标.
15.如图所示,动点 P 从坐标原点(0,0)出发,以每秒一个单位长度的速度按图中箭头所示方向运动,第1秒运动到点(1,0),第2秒运动到点(1,1),第3秒运动到点(0,1),第4秒运动到点(0,2)……则第2068秒,点 P 所在位置的坐标是 .
16.定义:在平面直角坐标系中,把从点 P 出发沿纵或横方向到达点 Q(至多拐一次弯)的路径长称为 P,Q的“实际距离”.如图所示,若 P(-1,1),Q(2,3),则 P,Q的“实际距离”为5,即PS+SQ=5或PT+TQ=5.如今环保低碳的共享单车已成为市民出行喜欢的交通工具,设A,B,C三个小区的坐标分别为A(3,1),B(5,-3),C(-1,-5),若点 M表示共享单车停放点,且满足M到A,B,C的“实际距离”相等,则点 M的坐标为 .
17.阅读材料,回答下列问题:
已知平面内两点M(x ,y ),N(x ,y ),则这两点间的距离可用下列公式计算:
例如:已知点 P(3,1),Q(1,-2),则这两点间的距离
特别地,如果两点M(x ,y ),N(x ,y )所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为 或
(1)已知A(1,2),B(-2,-3),试求A,B两点间的距离.
(2)已知点A,B在平行于y轴的同一条直线上,点A 的纵坐标为5,点B 的纵坐标为-1,试求A,B两点间的距离.
(3)已知△ABC的顶点坐标分别为A(0,4),B(-1,2),C(4,2),你能判定△ABC的形状吗 请说明理由.
1. B 2. D 3. D 4. B 5.9或-1 - 3 6.-97.(-2,0)
8.∵∠C=90°,AC=3,BC=4,
即点 B 的坐标为(5,0).过点C作CD⊥AB于点D,则
∴点 C的坐标为
9. C 10. A 11. C 12.2"+ -2
13.(1)本题建立平面直角坐标系答案不唯一.以直线 AB为x轴,直线 BC为y轴,点 B 为原点O 建立平面直角坐标系,如答图所示.
∵CD=3,BC=4,∴点 B(0,0),点 C(0,4),点D(-3,4).
过点 D作DE⊥AB于点E,则DE=BC=4.
∵AD=5,DE=4,∴AE= √AD -DE =3.
∴AB=AE+BE=3+3=6.∴点A(-6,0).
(2)取线段CD的中点M,线段AD的中点N.
∵C(0,4),D(-3,4),A(-6,0),
∴点 点
14.(1)∵|2a+b+1|+(a+2b-4) =0,
∴|2a+b+1|=0且
解得 即a=-2,b=3.
(2)如答图所示,过点 C作CT⊥x轴,CS⊥y轴,垂足分别为点 T,S.
∵A(-2,0),B(3,0),
∴AB=5.
∵C(-1,2),
∴CT=2,CS=1.
∴要使 则 即
∴点M的坐标为(0,5).
15.(45,43)16.(1,-2)
(2)AB=5--(-1)=6.
(3)△ABC为直角三角形.理由如下:
为直角三角形.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
