第5章 一次函数单元提优测试卷(含答案)2024-2025学年浙教版八年级数学上册
文档属性
| 名称 | 第5章 一次函数单元提优测试卷(含答案)2024-2025学年浙教版八年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 381.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第5章 一次函数单元提优测试卷
选择题
1.若正比例函数的图象经过点(2,--3),则这个图象必经过点( ).
A.(-3,-2) B.(2,3) C.(3,-2) D.(-2,3)
2.函数 的自变量x的取值范围是( ).
A. x≥2且x≠3 B. x≥2 C. x≠3 D. x>2且x≠3
3.如图所示,李老师早晨出门去锻炼,一段时间内沿⊙M 的半圆形M→A→C→B→M路径匀速慢跑,则李老师离出发点 M的距离与时间x之间的函数关系的大致图象是( ).
4.如图所示,已知直线y =x+m与.y = kx-1相交于点 P(-1,1),关于x的不等式x+m> kx-1的解集是( ).
A.x≥-1 B. x>-1 C.x≤-1 D. x<-1
5.如图所示,小亮从家出发步行到公交车站,等公交车,最后坐公交车到达学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系.有下列说法:①学校和小亮家的路程为8km;②小亮等公交车的时间为6min;③小亮步行的速度是 100m/ min;④公交车的速度是350m/ min;⑤小亮从家出发到学校共用了24min.其中正确的有( ).
A.2个 B.3个 C.4个 D.5个
6.已知直线y= kx-4(k<0)与两坐标轴围成的三角形面积为4,则直线的函数表达式为( ).
A. y=-x-4 B. y=-2x-4 C. y=-3x+4 D. y=-3x-4
7.若直线y=2x+3与y=3x-2b的交点在x轴上,则b的值是( ).
A. -3 D.6
8.函数y= kx+b(k≠0)中,当x的值增加2时,y的值减小3,则k的值为( ).
C. -2 D. -3
9.已知m=x+1,n=-x+2,若规定 则 y的最小值为( ).
A.0 B.1 C. -1 D.2
10.如图所示,直线l :y=x+1与直线 相交于点 P.直线l 与y轴交于点A.一动点C从点A 出发,先沿平行于x轴的方向运动,到达直线l 上的点 B 后,改为垂直于x轴的方向运动,到达直线l 上的点 A 后,再沿平行于x轴的方向运动,到达直线l 上的点 B 后,又改为垂直于x轴的方向运动……照此规律运动,动点C依次经过点B ,A ,B ,A ,…,B ,A ,…,!,则当动点 C到达A 处时,运动路径的总长为( ).
A.2020 C.22019+1
填空题
11.写出一个一次函数,使得该一次函数满足下列两个条件:①经过点(-1,1);②y随x的增大而增大.你写出的函数是 .
12.日常生活中,“老人”是一个模糊概念.有人想用“老人系数”来表示一个人的老年化程度,他设想“老人系数”的计算方法如下表:
人的年龄x(岁) x≤60 60该人的“老人系数” 0 x-60 1
按照这样的规定,一个70岁的人的“老人系数”为 .
13.如图1所示,在某个盛水容器内有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2所示的图象,则至少需要 s能把小水杯注满.
14.将y=-2x+4的图象向左平移 个单位长度,所得图象的函数表达式为 y=-2x.
15.设直线 交x轴于点A,交y轴于点B,如果点C在第四象限,且∠ABC=90°,AB=BC,那么点 C的坐标为 .
16.如图所示,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连结PC,将线段 PC绕点 P 顺时针旋转90°至线段 PD,过点 D 作直线AB⊥x轴,垂足为 B,直线AB与直线y=x交于点A,且BD=2AD,连结CD,直线CD与直线y=x交于点Q,则点Q的坐标为 .
三解答题
17.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人匀速跑的路程s(m)与时间t(s)之间的函数关系如图所示,结合图象解答下列问题:
(1)请你根据图象写出两条信息.
(2)求图中s 和 s。的值.
18.在平面直角坐标系中,一条直线经过A(-1,5),P(-2,a),B(3,-3)三点.
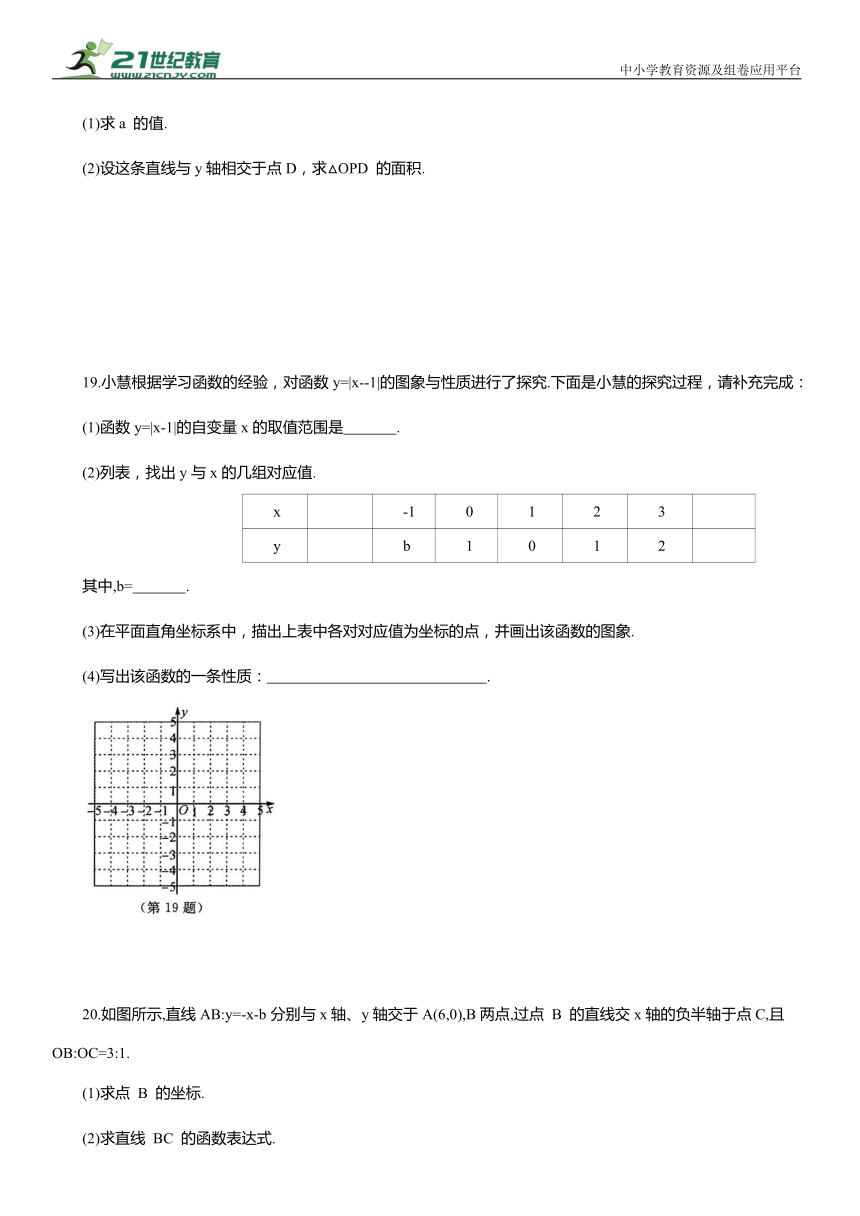
(1)求a 的值.
(2)设这条直线与y轴相交于点D,求△OPD 的面积.
19.小慧根据学习函数的经验,对函数y=|x--1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 .
(2)列表,找出y与x的几组对应值.
x -1 0 1 2 3
y b 1 0 1 2
其中,b= .
(3)在平面直角坐标系中,描出上表中各对对应值为坐标的点,并画出该函数的图象.
(4)写出该函数的一条性质: .
20.如图所示,直线AB:y=-x-b分别与x轴、y轴交于A(6,0),B两点,过点 B 的直线交x轴的负半轴于点C,且OB:OC=3:1.
(1)求点 B 的坐标.
(2)求直线 BC 的函数表达式.
(3)若点 P(m,2)在△ABC的内部,求m的取值范围.
21.某项工程若由甲、乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲、乙两队合作,则需12 天完成.
(1)甲、乙两队单独完成各需多少天
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)关于施工时间x(天)的函数表达式.
(3)在(2)的条件下,若施工期定为15~18天内完成(含15 和18天),如何安排施工方案使费用最少 最少费用为多少万元
22.如图1所示为甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(cm)与注水时间x(min)之间的函数关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线ABC 表示 槽中水的深度与注水时间之间的关系,线段 DE 表示 槽中水的深度与注水时间之间的函数关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙两个水槽中水的深度相同
(3)若乙槽底面积为 36cm (壁厚不计),求乙槽中铁块的体积.
(4)若乙槽中铁块的体积为112cm ,求甲槽底面积(壁厚不计).(直接写出结果)
23.如图所示,直线l:y=4-2x与x轴、y轴分别交于点A,B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点 D.
(1)求点 A,B的坐标以及直线m 的函数表达式.
(2)求四边形OAMD 的面积.
(3)若 P 是直线m 上一动点,试求OP+AP 的最小值.
(4)若点 N在x轴上,且△OMN是等腰三角形,请直接写出所有满足条件的点 N的坐标.
1. D 2. A 3. D 4. B 5. B 6. B 7. C 8. B9. B 10. B 11. y=x+2(答案不唯一) 12.0.513.5 14.2 15.(4,-4)
17.(1)由图象可得出:
①小刚比小明早到终点100s;
②两人匀速跑时,小刚的速度大于小明的速度.
18.(1)设直线的函数表达式为 y= kx+b,把A(-1,5),B(3,-3)代入,得 解得
∴直线的函数表达式为 y=-2x+3.
把 P(-2,a)代入 y=-2x+3得a=7.
(2)由(1)得点 P 的坐标为(-2,7).
令x=0,则y=3,∴D(0,3).
∴△OPD的面积
19.(1)任意实数
(2)2
(3)如答图所示.
(4)函数的最小值为0(答案不唯一)
20.(1)将点 A(6,0)代入直线 AB 的函数表达式可得0=-6-b,解得b=-6.
∴直线 AB的函数表达式为y=-x+6.
∴点 B 的坐标为(0,6).
(2)∵OB:OC=3:1,∴OC=2.
∴点C的坐标为(-2,0).
设直线 BC的函数表达式为 y= kx+6,则0=-2k+6,解得 k=3.
∴直线 BC的函数表达式为y=3x+6.
(3)把y=2代入y=-x+6得x=4;
把y=2代入y=3x+6得
结合图象可知,m的取值范围是
21.(1)设乙单独完成需a天,则甲单独完成需1.5a天.由题意得 解得a=20.
经检验:a=20是所列方程的解,且符合题意.
∴1.5a=30.
∴甲、乙两队单独完成分别需30天,20天.
(2)设甲、乙合作完成余下部分所需时间为ω天.
解得
(3)由题意得 解得5≤x≤10.
∴y随x的增大而减小.
∴当x=10时,
此时,甲先施工10天,再甲、乙合作8天,费用最低为38万元.
22.(1)乙 甲 乙槽中铁块的高度为14cm
(2)设线段AB,DE的函数表达式分别为: ∵AB 经过点(0,2)和(4,14),DE经过点(0,12)和(6,0),
解得
令3x+2=-2x+12,解得x=2.
∴当2min时两个水槽水面一样高.
(3)由图象知:当乙槽中水面没有没过铁块时4min水面上升了12cm,即1min上升3cm,
当水面没过铁块时,2min上升了5cm,即 1min 上升2.5cm,
设铁块的底面积为a(cm ),
则乙水槽中不放铁块的体积为:2.5×36cm ,放了铁块的体积为3×(36-a)cm ,
∴3×(36-a)=2.5×36,解得a=6.
∴铁块的体积为:6×14=84(cm ).
(4)60cm .∵铁块的体积为112cm ,
∴铁块的底面积为
可设甲槽的底面积为 m(cm ),乙槽的底面积为n(cm ),则根据前4min 和后 2min 甲槽中流出的水的体积和乙槽中流入的水的体积分别相等列二元一次方程组,
得 解得m=60.
23.(1)在y=4-2x中,令x=0,解得y=4,∴点 B的坐标是(0,4),令 y=0,∴4-2x=0,解得x=2,则点 A的坐标是(2,0).设直线 m的函数表达式为y= kx+b.
解得
∴直线m的函数表达式为y=x+1.
(2)如答图所示,作 ME⊥x轴于点 E,则点 E 的坐标是(1,0),ME=2,AE=1.易知OD=1.
(3)经过点 O且与直线 m垂直的直线的函数表达式为y=-x,
由题意得 解得
∴直 线 y = x 和 直 线 m 的 交 点 坐 标 是
设点O关于直线m的对称点的坐标是(m,n),解得 ∴点O关于直线m的对称点坐标是(-1,1).∴OP+AP 最小值是:
当O是顶角顶点时,点N 的坐标是 或 ( ,0);
当M是顶角顶点时,ME是点O 和N 的对称轴,则点 N 的坐标是(2,0);
当N是顶角顶点时,OM的中点坐标是( ,1),设直线OM的函数表达式为y= ax,则把(1,2)代入函数表达式得:a=2,即函数表达式为y=2x,
则经过OM 的中点,且与OM垂直的直线的函数表达式为 则 解得b= ,则直线的函数表达式为 令 y=0,解得 则点 N的坐标是( ,0).综上所述,点N 的坐标是
(- ,0),( ,0),(2,0)或( ,0).
第5章 一次函数单元提优测试卷
选择题
1.若正比例函数的图象经过点(2,--3),则这个图象必经过点( ).
A.(-3,-2) B.(2,3) C.(3,-2) D.(-2,3)
2.函数 的自变量x的取值范围是( ).
A. x≥2且x≠3 B. x≥2 C. x≠3 D. x>2且x≠3
3.如图所示,李老师早晨出门去锻炼,一段时间内沿⊙M 的半圆形M→A→C→B→M路径匀速慢跑,则李老师离出发点 M的距离与时间x之间的函数关系的大致图象是( ).
4.如图所示,已知直线y =x+m与.y = kx-1相交于点 P(-1,1),关于x的不等式x+m> kx-1的解集是( ).
A.x≥-1 B. x>-1 C.x≤-1 D. x<-1
5.如图所示,小亮从家出发步行到公交车站,等公交车,最后坐公交车到达学校,图中的折线表示小亮的行程s(km)与所花时间t(min)之间的函数关系.有下列说法:①学校和小亮家的路程为8km;②小亮等公交车的时间为6min;③小亮步行的速度是 100m/ min;④公交车的速度是350m/ min;⑤小亮从家出发到学校共用了24min.其中正确的有( ).
A.2个 B.3个 C.4个 D.5个
6.已知直线y= kx-4(k<0)与两坐标轴围成的三角形面积为4,则直线的函数表达式为( ).
A. y=-x-4 B. y=-2x-4 C. y=-3x+4 D. y=-3x-4
7.若直线y=2x+3与y=3x-2b的交点在x轴上,则b的值是( ).
A. -3 D.6
8.函数y= kx+b(k≠0)中,当x的值增加2时,y的值减小3,则k的值为( ).
C. -2 D. -3
9.已知m=x+1,n=-x+2,若规定 则 y的最小值为( ).
A.0 B.1 C. -1 D.2
10.如图所示,直线l :y=x+1与直线 相交于点 P.直线l 与y轴交于点A.一动点C从点A 出发,先沿平行于x轴的方向运动,到达直线l 上的点 B 后,改为垂直于x轴的方向运动,到达直线l 上的点 A 后,再沿平行于x轴的方向运动,到达直线l 上的点 B 后,又改为垂直于x轴的方向运动……照此规律运动,动点C依次经过点B ,A ,B ,A ,…,B ,A ,…,!,则当动点 C到达A 处时,运动路径的总长为( ).
A.2020 C.22019+1
填空题
11.写出一个一次函数,使得该一次函数满足下列两个条件:①经过点(-1,1);②y随x的增大而增大.你写出的函数是 .
12.日常生活中,“老人”是一个模糊概念.有人想用“老人系数”来表示一个人的老年化程度,他设想“老人系数”的计算方法如下表:
人的年龄x(岁) x≤60 60
按照这样的规定,一个70岁的人的“老人系数”为 .
13.如图1所示,在某个盛水容器内有一个小水杯,小水杯内有部分水,现在匀速持续地向小水杯内注水,注满小水杯后,继续注水,小水杯内水的高度y(cm)和注水时间x(s)之间的关系满足如图2所示的图象,则至少需要 s能把小水杯注满.
14.将y=-2x+4的图象向左平移 个单位长度,所得图象的函数表达式为 y=-2x.
15.设直线 交x轴于点A,交y轴于点B,如果点C在第四象限,且∠ABC=90°,AB=BC,那么点 C的坐标为 .
16.如图所示,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连结PC,将线段 PC绕点 P 顺时针旋转90°至线段 PD,过点 D 作直线AB⊥x轴,垂足为 B,直线AB与直线y=x交于点A,且BD=2AD,连结CD,直线CD与直线y=x交于点Q,则点Q的坐标为 .
三解答题
17.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m,此后两人匀速跑的路程s(m)与时间t(s)之间的函数关系如图所示,结合图象解答下列问题:
(1)请你根据图象写出两条信息.
(2)求图中s 和 s。的值.
18.在平面直角坐标系中,一条直线经过A(-1,5),P(-2,a),B(3,-3)三点.
(1)求a 的值.
(2)设这条直线与y轴相交于点D,求△OPD 的面积.
19.小慧根据学习函数的经验,对函数y=|x--1|的图象与性质进行了探究.下面是小慧的探究过程,请补充完成:
(1)函数y=|x-1|的自变量x的取值范围是 .
(2)列表,找出y与x的几组对应值.
x -1 0 1 2 3
y b 1 0 1 2
其中,b= .
(3)在平面直角坐标系中,描出上表中各对对应值为坐标的点,并画出该函数的图象.
(4)写出该函数的一条性质: .
20.如图所示,直线AB:y=-x-b分别与x轴、y轴交于A(6,0),B两点,过点 B 的直线交x轴的负半轴于点C,且OB:OC=3:1.
(1)求点 B 的坐标.
(2)求直线 BC 的函数表达式.
(3)若点 P(m,2)在△ABC的内部,求m的取值范围.
21.某项工程若由甲、乙两队分别单独完成,则甲队用时是乙队的1.5倍;若由甲、乙两队合作,则需12 天完成.
(1)甲、乙两队单独完成各需多少天
(2)若施工方案是甲先单独施工x天,剩下工程甲、乙合作完成,若甲队施工费用为每天1万元,乙队施工费用为每天2.5万元,求施工总费用y(万元)关于施工时间x(天)的函数表达式.
(3)在(2)的条件下,若施工期定为15~18天内完成(含15 和18天),如何安排施工方案使费用最少 最少费用为多少万元
22.如图1所示为甲、乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形铁块立放其中(圆柱形铁块的下底面完全落在乙槽底面上).现将甲槽中的水匀速注入乙槽,甲、乙两个水槽中水的深度y(cm)与注水时间x(min)之间的函数关系如图2所示.根据图象提供的信息,解答下列问题:
(1)图2中折线ABC 表示 槽中水的深度与注水时间之间的关系,线段 DE 表示 槽中水的深度与注水时间之间的函数关系(以上两空选填“甲”或“乙”),点B的纵坐标表示的实际意义是 .
(2)注水多长时间时,甲、乙两个水槽中水的深度相同
(3)若乙槽底面积为 36cm (壁厚不计),求乙槽中铁块的体积.
(4)若乙槽中铁块的体积为112cm ,求甲槽底面积(壁厚不计).(直接写出结果)
23.如图所示,直线l:y=4-2x与x轴、y轴分别交于点A,B,且与直线m相交于点M(1,2),已知直线m经过点C(-1,0),且与y轴交于点 D.
(1)求点 A,B的坐标以及直线m 的函数表达式.
(2)求四边形OAMD 的面积.
(3)若 P 是直线m 上一动点,试求OP+AP 的最小值.
(4)若点 N在x轴上,且△OMN是等腰三角形,请直接写出所有满足条件的点 N的坐标.
1. D 2. A 3. D 4. B 5. B 6. B 7. C 8. B9. B 10. B 11. y=x+2(答案不唯一) 12.0.513.5 14.2 15.(4,-4)
17.(1)由图象可得出:
①小刚比小明早到终点100s;
②两人匀速跑时,小刚的速度大于小明的速度.
18.(1)设直线的函数表达式为 y= kx+b,把A(-1,5),B(3,-3)代入,得 解得
∴直线的函数表达式为 y=-2x+3.
把 P(-2,a)代入 y=-2x+3得a=7.
(2)由(1)得点 P 的坐标为(-2,7).
令x=0,则y=3,∴D(0,3).
∴△OPD的面积
19.(1)任意实数
(2)2
(3)如答图所示.
(4)函数的最小值为0(答案不唯一)
20.(1)将点 A(6,0)代入直线 AB 的函数表达式可得0=-6-b,解得b=-6.
∴直线 AB的函数表达式为y=-x+6.
∴点 B 的坐标为(0,6).
(2)∵OB:OC=3:1,∴OC=2.
∴点C的坐标为(-2,0).
设直线 BC的函数表达式为 y= kx+6,则0=-2k+6,解得 k=3.
∴直线 BC的函数表达式为y=3x+6.
(3)把y=2代入y=-x+6得x=4;
把y=2代入y=3x+6得
结合图象可知,m的取值范围是
21.(1)设乙单独完成需a天,则甲单独完成需1.5a天.由题意得 解得a=20.
经检验:a=20是所列方程的解,且符合题意.
∴1.5a=30.
∴甲、乙两队单独完成分别需30天,20天.
(2)设甲、乙合作完成余下部分所需时间为ω天.
解得
(3)由题意得 解得5≤x≤10.
∴y随x的增大而减小.
∴当x=10时,
此时,甲先施工10天,再甲、乙合作8天,费用最低为38万元.
22.(1)乙 甲 乙槽中铁块的高度为14cm
(2)设线段AB,DE的函数表达式分别为: ∵AB 经过点(0,2)和(4,14),DE经过点(0,12)和(6,0),
解得
令3x+2=-2x+12,解得x=2.
∴当2min时两个水槽水面一样高.
(3)由图象知:当乙槽中水面没有没过铁块时4min水面上升了12cm,即1min上升3cm,
当水面没过铁块时,2min上升了5cm,即 1min 上升2.5cm,
设铁块的底面积为a(cm ),
则乙水槽中不放铁块的体积为:2.5×36cm ,放了铁块的体积为3×(36-a)cm ,
∴3×(36-a)=2.5×36,解得a=6.
∴铁块的体积为:6×14=84(cm ).
(4)60cm .∵铁块的体积为112cm ,
∴铁块的底面积为
可设甲槽的底面积为 m(cm ),乙槽的底面积为n(cm ),则根据前4min 和后 2min 甲槽中流出的水的体积和乙槽中流入的水的体积分别相等列二元一次方程组,
得 解得m=60.
23.(1)在y=4-2x中,令x=0,解得y=4,∴点 B的坐标是(0,4),令 y=0,∴4-2x=0,解得x=2,则点 A的坐标是(2,0).设直线 m的函数表达式为y= kx+b.
解得
∴直线m的函数表达式为y=x+1.
(2)如答图所示,作 ME⊥x轴于点 E,则点 E 的坐标是(1,0),ME=2,AE=1.易知OD=1.
(3)经过点 O且与直线 m垂直的直线的函数表达式为y=-x,
由题意得 解得
∴直 线 y = x 和 直 线 m 的 交 点 坐 标 是
设点O关于直线m的对称点的坐标是(m,n),解得 ∴点O关于直线m的对称点坐标是(-1,1).∴OP+AP 最小值是:
当O是顶角顶点时,点N 的坐标是 或 ( ,0);
当M是顶角顶点时,ME是点O 和N 的对称轴,则点 N 的坐标是(2,0);
当N是顶角顶点时,OM的中点坐标是( ,1),设直线OM的函数表达式为y= ax,则把(1,2)代入函数表达式得:a=2,即函数表达式为y=2x,
则经过OM 的中点,且与OM垂直的直线的函数表达式为 则 解得b= ,则直线的函数表达式为 令 y=0,解得 则点 N的坐标是( ,0).综上所述,点N 的坐标是
(- ,0),( ,0),(2,0)或( ,0).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
