专题复习二 一次函数的应用与综合 同步练习(含答案)
文档属性
| 名称 | 专题复习二 一次函数的应用与综合 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 375.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 23:11:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习二 一次函数的应用与综合
1.某工厂2020年的产值为23万元,计划从2021年开始,每年增加2万元,则年产值y(万元)关于经过的年数x的函数表达式为( ).
A. y=2x--23 B. y=23x+2 C. y=2x+23 D. y=23x--2
2.已知直线l :y=-3x+b与直线l :y=-kx+1在同一平面直角坐标系中的图象交于点(1,-2),则方程组 的解是( ).
3.某地现有绿地9万公顷,由于植被遭到严重破坏,土地沙化速度竟达每年0.3万公顷.照此速度发展下去,设t年后该地剩余绿地面积为S万公顷.下列图象中,能正确反映S与t之间的函数关系的是( ).
4.蓄水池中装有一个进水管和一个出水管,单位时间内进、出水量都一定,先打开进水管10min后再两管同时开放12min,然后关闭进水管,直至把池中的水放完.池中的蓄水量y(L)随时间x(min)变化的图象如图所示,则池中的水放完的时间是( ).
A.第24min B.第26min C.第28min D.第30min
5.如图所示为某航空公司托运行李的费用y(元)与托运行李的质量x(kg)之间的函数关系,由图中数据可知,行李的质量只要不超过 kg,就可以免费托运.
6.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如下表.现有15升食物需要存放且要求每个盒子要装满,由于 A 型号盒子正在做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需的最少费用为 元.
型号 A B
单个盒子容量(升) 2 3
单价(元) 5 6
7.为了加强市民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格如右表.
(1)设某用户月用水量为x(m ),缴纳水费y(元),x与y之间的函数关系图象如图所示,求a的值及y关于x的函数表达式.
每月用水量(m ) 单价(元/m )
不超出10m 的部分 a
超出10m 的部分 a+2
(2)在(1)的条件下,若该户居民3,4月共用水 20m ,且4月用水量超过3月,共缴纳水费42元,则该户居民3,4月各用水多少立方米
8.今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x 1 2 3 4
水位 y(m) 20.00 20.50 21.00 21.50
(1)请建立该水库水位y与日期x之间的函数模型.
(2)请用求出的函数表达式预测该水库今年4月6日的水位.
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗
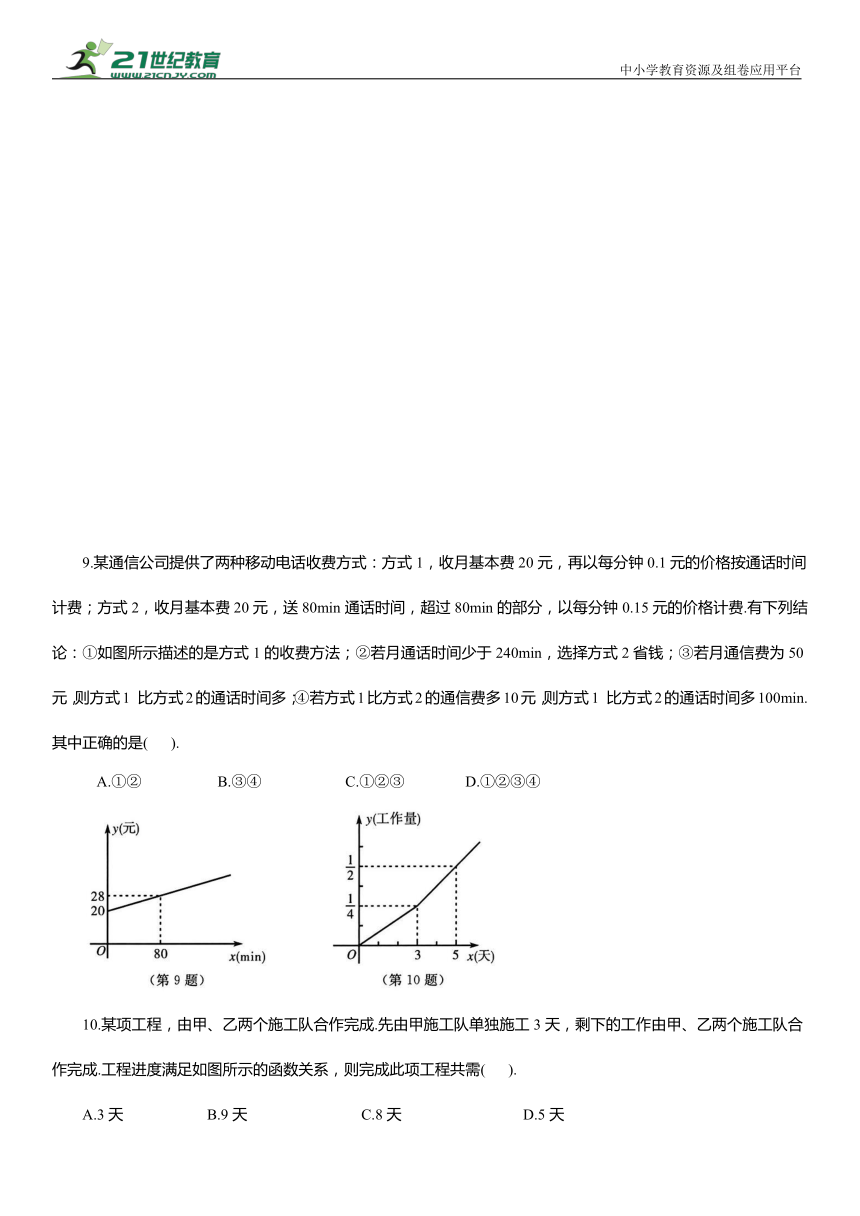
9.某通信公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80min通话时间,超过80min的部分,以每分钟0.15元的价格计费.有下列结论:①如图所示描述的是方式1的收费方法;②若月通话时间少于240min,选择方式2省钱;③若月通信费为50元,则方式1 比方式2的通话时间多;④若方式1比方式2的通信费多10元,则方式1 比方式2的通话时间多100min.其中正确的是( ).
A.①② B.③④ C.①②③ D.①②③④
10.某项工程,由甲、乙两个施工队合作完成.先由甲施工队单独施工3天,剩下的工作由甲、乙两个施工队合作完成.工程进度满足如图所示的函数关系,则完成此项工程共需( ).
A.3天 B.9天 C.8天 D.5天
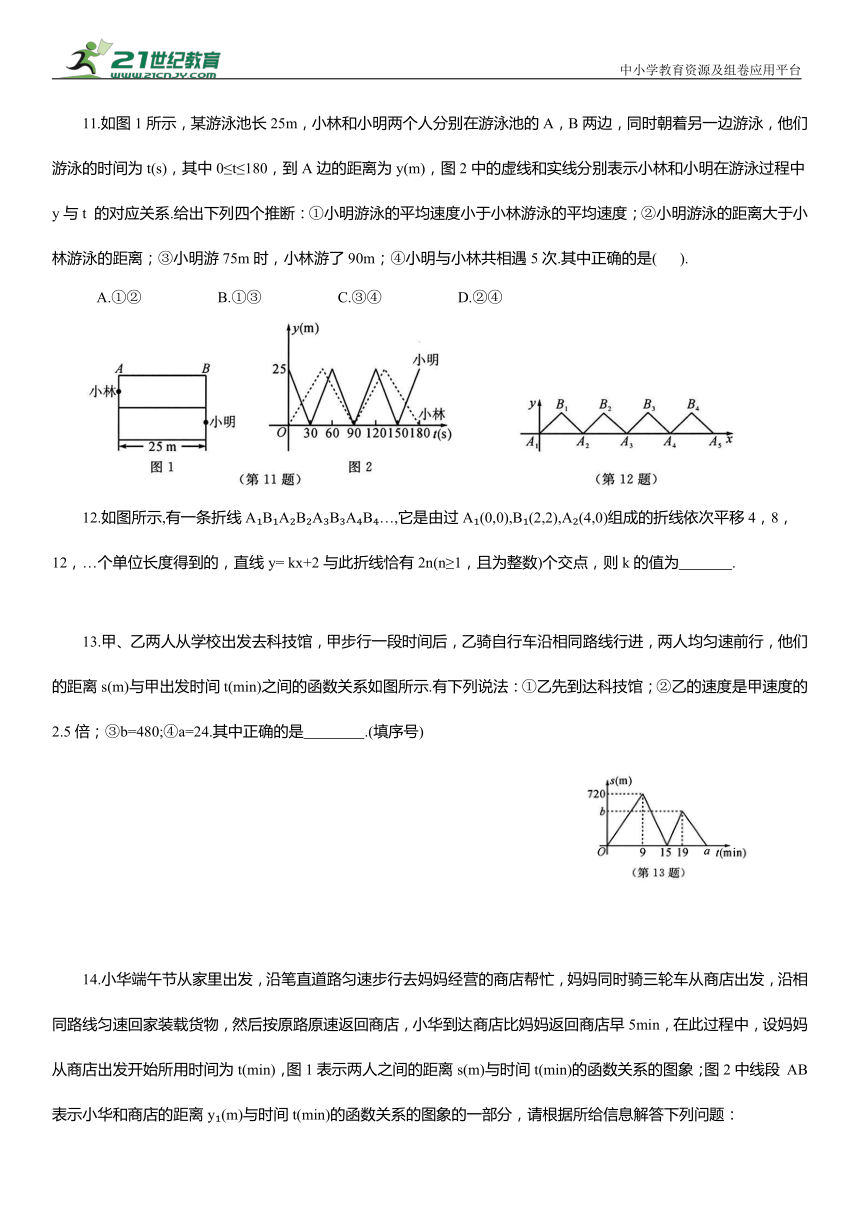
11.如图1所示,某游泳池长25m,小林和小明两个人分别在游泳池的A,B两边,同时朝着另一边游泳,他们游泳的时间为t(s),其中0≤t≤180,到A边的距离为y(m),图2中的虚线和实线分别表示小林和小明在游泳过程中y与t 的对应关系.给出下列四个推断:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的距离大于小林游泳的距离;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中正确的是( ).
A.①② B.①③ C.③④ D.②④
12.如图所示,有一条折线A B A B A B A B …,它是由过A (0,0),B (2,2),A (4,0)组成的折线依次平移4,8,12,…个单位长度得到的,直线y= kx+2与此折线恰有2n(n≥1,且为整数)个交点,则k的值为 .
13.甲、乙两人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的距离s(m)与甲出发时间t(min)之间的函数关系如图所示.有下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 .(填序号)
14.小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5min,在此过程中,设妈妈从商店出发开始所用时间为t(min),图1表示两人之间的距离s(m)与时间t(min)的函数关系的图象;图2中线段 AB 表示小华和商店的距离y (m)与时间t(min)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(1)填空:妈妈骑车的速度是 m/ min,妈妈在家装载货物所用时间是 min,点 M 的坐标是 .
(2)直接写出妈妈和商店的距离y (m)与时间t(min)的函数表达式,并在图2中画出其函数图象.
(3)求t为何值时,两人相距360m.
15.在某电视节目中,王清和李北远程控制无人驾驶汽车运送货物,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达 B地后,停留3s卸货,然后原路返回A地,慢车到达A地即停运休息,如图所示为两车之间的距离 y(m)与行驶时间x(s)的函数图象,根据图象信息,计算a,b的值分别为( ).
A.39,26 B.39,26.4 C.38,26 D.38,26.4
16.某商场准备购进A,B两种型号电脑,每台A 型号电脑进价比每台B 型号电脑多500元,用40000元购进A型号电脑的数量与用30000元购进B型号电脑的数量相同,请解答下列问题:
(1)A,B型号电脑每台进价各是多少元
(2)若每台A型号电脑售价为2500元,每台B型号电脑售价为1800元,商场决定同时购进A,B两种型号电脑20台,且全部售出,请写出所获的利润y(单位:元)与A型号电脑x(单位:台)之间的函数表达式,若商场用不超过36000元购进A,B两种型号电脑,A型号电脑至少购进10台,则有几种购买方案
(3)在(2)的条件下,将不超过所获得的最大利润再次购买A,B两种型号电脑捐赠给某个福利院,请直接写出捐赠A,B两种型号电脑总数最多是多少台.
17.如图所示,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且 BC⊥OC 于点C,点 A 的坐标为( ,D 是线段OC 上一点,且OD=4,连结AD.
(1)求证:△AOD 是等边三角形.
(2)求点 B 的坐标.
(3)平行于AD的直线l从原点O 出发,沿x轴正方向平移.设直线l被四边形OABC 截得的线段长为m,直线l与x 轴交点的横坐标为t.
①当直线l与x轴的交点在线段CD 上(交点不与点 C,D重合)时,请直接写出m 关于t的函数表达式.(不必写出自变量t的取值范围)
②若m=2,请直接写出此时直线l与x轴的交点坐标.
专题复习二 一次函数的应用与综合
1. C 2. A 3. C 4. C 5.20 6.29
当0≤x≤10时,y关于x的函数表达式为y=2x.当x>10时,设y关于x的函数表达式为y= kx+b,则 解得
∴y关于x的函数表达式为y=4x-20.
综上可得, y关 于 x 的 函 数 表 达 式 为 y =
(2)设3月用水 z(m ),则4月用水( 由题意得2z+4(20-z)-20=42,解得 z=9.
∴20-9=11(m ).
∴3月用水 9m ,4月用水 11m .
8.(1)因为水库的水位 y随日期x 的变化是均匀的,所以水位y与日期x之间的函数为一次函数,设 y = kx+b,把(1,20)和(2,20.5)代 入得 解得
∴y=0.5x+19.5.
(2)当x=6时,y=0.5×6+19.5=22.5.
(3)不能.理由如下:
∵12月远大于4月,
∴所建立的函数模型远离已知数据,作预测是不可靠的.
9. C 10. B 11. D 12.- 13.①②③
14.(1)120 5 (20,1200)
其图象如答图所示.
(3)由题意可知:小华速度为 60m/ min,妈妈速度为120m/ min.
①相遇前,依题意有60t+120t+360=1800,解得 t=8min.
②相遇后,依题意有60t+120t-360=1800,解得 t=12min.
③依题意,当t=20min时,妈妈从家里出发开始追赶小华,
依题意有--120t+4200=360,解得 t=32min.
∴当t=8,12或32min时,两人相距360m.
15. B
16.(1)设每台 A 型号电脑进价为a 元,每台 B 型号电脑进价为(a-500)元,由题意,得 解得a=2000.经检验a=2000是原方程的解,且符合题意.
∴2000-500=1500(元).
∴每台 A 型号电脑进价为 2000元,每台 B 型号电脑进价为1500元.
(2)由题意得 y=(2500 - 2000)x+(1800 -1500)(20-x)=200x+6000,
∵2000x+1500(20-x)≤36000,∴x≤12.
又∵x≥10,∴10≤x≤12.
∵x是整数,∴x=10,11,12.
∴有三种购买方案.
(3)∵y=200x+6000 是一次函数,y随x的增大而增大,
∴当x=12 时,y有最大值=12×200+6000=8400(元).
设再次购买A型电脑b台,B型电脑c台,
∴2000b+1500c≤8400,且 b,c为非负整数.
∴b=0,c=5或b=1,c=4或b=2,c=2或b=3,c=1或b=4,c=0.
∴捐赠A,B两种型号电脑总数最多是5台.
17.(1)如答图1 所示,过点A作AM⊥x轴于点M,∵点 A 的坐标为((2,2 ),∴OM=2,AM=2
由 勾 股 定 理 得, OA =
∵OD=4,∴MD=2,AD=
∴OA=OD=AD,即△AOD是等边三角形.
(2)如答图1所示,过点 A 作AN⊥BC于点 N.
∵BC⊥OC,AM⊥x轴,
∴∠BCM=∠CMA=∠ANC=90°.
∴四边形ANCM为矩形.∴AN=MC,AM=NC.
∵∠B=60°,AB=4 ,∴在 Rt△ABN中,
∴AN=MC=6,CN=AM=2
∴OC=OM+MC=2+6=8,
∴点 B 的坐标为((8,4 ).
(3)①如答图2 所示, ②如答图3所示,(2,0),( ,0).
专题复习二 一次函数的应用与综合
1.某工厂2020年的产值为23万元,计划从2021年开始,每年增加2万元,则年产值y(万元)关于经过的年数x的函数表达式为( ).
A. y=2x--23 B. y=23x+2 C. y=2x+23 D. y=23x--2
2.已知直线l :y=-3x+b与直线l :y=-kx+1在同一平面直角坐标系中的图象交于点(1,-2),则方程组 的解是( ).
3.某地现有绿地9万公顷,由于植被遭到严重破坏,土地沙化速度竟达每年0.3万公顷.照此速度发展下去,设t年后该地剩余绿地面积为S万公顷.下列图象中,能正确反映S与t之间的函数关系的是( ).
4.蓄水池中装有一个进水管和一个出水管,单位时间内进、出水量都一定,先打开进水管10min后再两管同时开放12min,然后关闭进水管,直至把池中的水放完.池中的蓄水量y(L)随时间x(min)变化的图象如图所示,则池中的水放完的时间是( ).
A.第24min B.第26min C.第28min D.第30min
5.如图所示为某航空公司托运行李的费用y(元)与托运行李的质量x(kg)之间的函数关系,由图中数据可知,行李的质量只要不超过 kg,就可以免费托运.
6.一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如下表.现有15升食物需要存放且要求每个盒子要装满,由于 A 型号盒子正在做促销活动:购买三个及三个以上可一次性返还现金4元,则一次性购买盒子所需的最少费用为 元.
型号 A B
单个盒子容量(升) 2 3
单价(元) 5 6
7.为了加强市民的节水意识,合理利用水资源,某市采用价格调控手段达到节水的目的.该市自来水收费价格如右表.
(1)设某用户月用水量为x(m ),缴纳水费y(元),x与y之间的函数关系图象如图所示,求a的值及y关于x的函数表达式.
每月用水量(m ) 单价(元/m )
不超出10m 的部分 a
超出10m 的部分 a+2
(2)在(1)的条件下,若该户居民3,4月共用水 20m ,且4月用水量超过3月,共缴纳水费42元,则该户居民3,4月各用水多少立方米
8.今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
日期x 1 2 3 4
水位 y(m) 20.00 20.50 21.00 21.50
(1)请建立该水库水位y与日期x之间的函数模型.
(2)请用求出的函数表达式预测该水库今年4月6日的水位.
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗
9.某通信公司提供了两种移动电话收费方式:方式1,收月基本费20元,再以每分钟0.1元的价格按通话时间计费;方式2,收月基本费20元,送80min通话时间,超过80min的部分,以每分钟0.15元的价格计费.有下列结论:①如图所示描述的是方式1的收费方法;②若月通话时间少于240min,选择方式2省钱;③若月通信费为50元,则方式1 比方式2的通话时间多;④若方式1比方式2的通信费多10元,则方式1 比方式2的通话时间多100min.其中正确的是( ).
A.①② B.③④ C.①②③ D.①②③④
10.某项工程,由甲、乙两个施工队合作完成.先由甲施工队单独施工3天,剩下的工作由甲、乙两个施工队合作完成.工程进度满足如图所示的函数关系,则完成此项工程共需( ).
A.3天 B.9天 C.8天 D.5天
11.如图1所示,某游泳池长25m,小林和小明两个人分别在游泳池的A,B两边,同时朝着另一边游泳,他们游泳的时间为t(s),其中0≤t≤180,到A边的距离为y(m),图2中的虚线和实线分别表示小林和小明在游泳过程中y与t 的对应关系.给出下列四个推断:①小明游泳的平均速度小于小林游泳的平均速度;②小明游泳的距离大于小林游泳的距离;③小明游75m时,小林游了90m;④小明与小林共相遇5次.其中正确的是( ).
A.①② B.①③ C.③④ D.②④
12.如图所示,有一条折线A B A B A B A B …,它是由过A (0,0),B (2,2),A (4,0)组成的折线依次平移4,8,12,…个单位长度得到的,直线y= kx+2与此折线恰有2n(n≥1,且为整数)个交点,则k的值为 .
13.甲、乙两人从学校出发去科技馆,甲步行一段时间后,乙骑自行车沿相同路线行进,两人均匀速前行,他们的距离s(m)与甲出发时间t(min)之间的函数关系如图所示.有下列说法:①乙先到达科技馆;②乙的速度是甲速度的2.5倍;③b=480;④a=24.其中正确的是 .(填序号)
14.小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5min,在此过程中,设妈妈从商店出发开始所用时间为t(min),图1表示两人之间的距离s(m)与时间t(min)的函数关系的图象;图2中线段 AB 表示小华和商店的距离y (m)与时间t(min)的函数关系的图象的一部分,请根据所给信息解答下列问题:
(1)填空:妈妈骑车的速度是 m/ min,妈妈在家装载货物所用时间是 min,点 M 的坐标是 .
(2)直接写出妈妈和商店的距离y (m)与时间t(min)的函数表达式,并在图2中画出其函数图象.
(3)求t为何值时,两人相距360m.
15.在某电视节目中,王清和李北远程控制无人驾驶汽车运送货物,王清操控的快车和李北操控的慢车分别从A,B两地同时出发,相向而行.快车到达 B地后,停留3s卸货,然后原路返回A地,慢车到达A地即停运休息,如图所示为两车之间的距离 y(m)与行驶时间x(s)的函数图象,根据图象信息,计算a,b的值分别为( ).
A.39,26 B.39,26.4 C.38,26 D.38,26.4
16.某商场准备购进A,B两种型号电脑,每台A 型号电脑进价比每台B 型号电脑多500元,用40000元购进A型号电脑的数量与用30000元购进B型号电脑的数量相同,请解答下列问题:
(1)A,B型号电脑每台进价各是多少元
(2)若每台A型号电脑售价为2500元,每台B型号电脑售价为1800元,商场决定同时购进A,B两种型号电脑20台,且全部售出,请写出所获的利润y(单位:元)与A型号电脑x(单位:台)之间的函数表达式,若商场用不超过36000元购进A,B两种型号电脑,A型号电脑至少购进10台,则有几种购买方案
(3)在(2)的条件下,将不超过所获得的最大利润再次购买A,B两种型号电脑捐赠给某个福利院,请直接写出捐赠A,B两种型号电脑总数最多是多少台.
17.如图所示,在平面直角坐标系中,四边形OABC的顶点O为坐标原点,点C在x轴的正半轴上,且 BC⊥OC 于点C,点 A 的坐标为( ,D 是线段OC 上一点,且OD=4,连结AD.
(1)求证:△AOD 是等边三角形.
(2)求点 B 的坐标.
(3)平行于AD的直线l从原点O 出发,沿x轴正方向平移.设直线l被四边形OABC 截得的线段长为m,直线l与x 轴交点的横坐标为t.
①当直线l与x轴的交点在线段CD 上(交点不与点 C,D重合)时,请直接写出m 关于t的函数表达式.(不必写出自变量t的取值范围)
②若m=2,请直接写出此时直线l与x轴的交点坐标.
专题复习二 一次函数的应用与综合
1. C 2. A 3. C 4. C 5.20 6.29
当0≤x≤10时,y关于x的函数表达式为y=2x.当x>10时,设y关于x的函数表达式为y= kx+b,则 解得
∴y关于x的函数表达式为y=4x-20.
综上可得, y关 于 x 的 函 数 表 达 式 为 y =
(2)设3月用水 z(m ),则4月用水( 由题意得2z+4(20-z)-20=42,解得 z=9.
∴20-9=11(m ).
∴3月用水 9m ,4月用水 11m .
8.(1)因为水库的水位 y随日期x 的变化是均匀的,所以水位y与日期x之间的函数为一次函数,设 y = kx+b,把(1,20)和(2,20.5)代 入得 解得
∴y=0.5x+19.5.
(2)当x=6时,y=0.5×6+19.5=22.5.
(3)不能.理由如下:
∵12月远大于4月,
∴所建立的函数模型远离已知数据,作预测是不可靠的.
9. C 10. B 11. D 12.- 13.①②③
14.(1)120 5 (20,1200)
其图象如答图所示.
(3)由题意可知:小华速度为 60m/ min,妈妈速度为120m/ min.
①相遇前,依题意有60t+120t+360=1800,解得 t=8min.
②相遇后,依题意有60t+120t-360=1800,解得 t=12min.
③依题意,当t=20min时,妈妈从家里出发开始追赶小华,
依题意有--120t+4200=360,解得 t=32min.
∴当t=8,12或32min时,两人相距360m.
15. B
16.(1)设每台 A 型号电脑进价为a 元,每台 B 型号电脑进价为(a-500)元,由题意,得 解得a=2000.经检验a=2000是原方程的解,且符合题意.
∴2000-500=1500(元).
∴每台 A 型号电脑进价为 2000元,每台 B 型号电脑进价为1500元.
(2)由题意得 y=(2500 - 2000)x+(1800 -1500)(20-x)=200x+6000,
∵2000x+1500(20-x)≤36000,∴x≤12.
又∵x≥10,∴10≤x≤12.
∵x是整数,∴x=10,11,12.
∴有三种购买方案.
(3)∵y=200x+6000 是一次函数,y随x的增大而增大,
∴当x=12 时,y有最大值=12×200+6000=8400(元).
设再次购买A型电脑b台,B型电脑c台,
∴2000b+1500c≤8400,且 b,c为非负整数.
∴b=0,c=5或b=1,c=4或b=2,c=2或b=3,c=1或b=4,c=0.
∴捐赠A,B两种型号电脑总数最多是5台.
17.(1)如答图1 所示,过点A作AM⊥x轴于点M,∵点 A 的坐标为((2,2 ),∴OM=2,AM=2
由 勾 股 定 理 得, OA =
∵OD=4,∴MD=2,AD=
∴OA=OD=AD,即△AOD是等边三角形.
(2)如答图1所示,过点 A 作AN⊥BC于点 N.
∵BC⊥OC,AM⊥x轴,
∴∠BCM=∠CMA=∠ANC=90°.
∴四边形ANCM为矩形.∴AN=MC,AM=NC.
∵∠B=60°,AB=4 ,∴在 Rt△ABN中,
∴AN=MC=6,CN=AM=2
∴OC=OM+MC=2+6=8,
∴点 B 的坐标为((8,4 ).
(3)①如答图2 所示, ②如答图3所示,(2,0),( ,0).
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
