5.5 一次函数的简单应用(2) 同步练习(含答案)
文档属性
| 名称 | 5.5 一次函数的简单应用(2) 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 393.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
5.5 一次函数的简单应用(2)
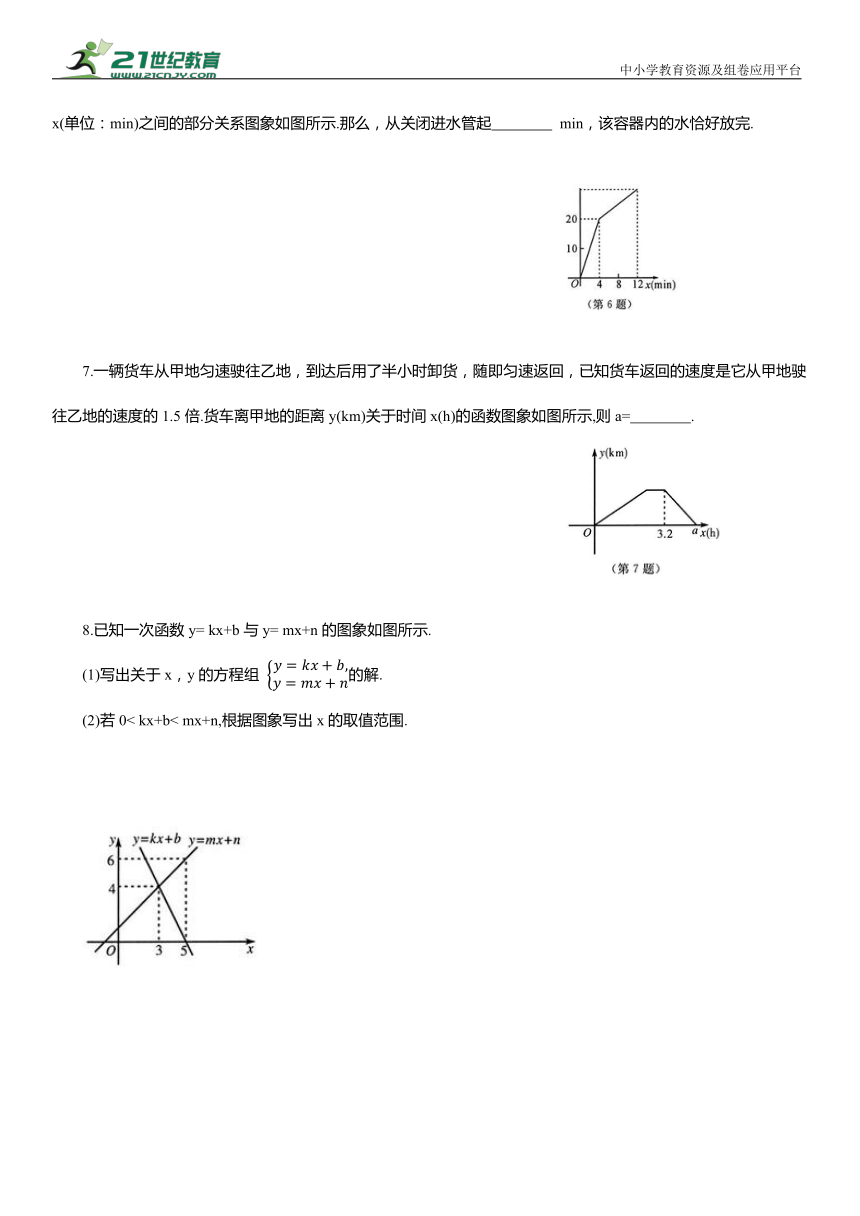
1.某商户以每件8元的价格购进若干件“四季如春植绒窗花”到市场去销售,销售金额y(元)与销售量x(件)之间的函数关系的图象如图所示,则降价后每件商品销售的价格为( ).
A.5元 B.10元 C.12.5元 D.15元
2.如图所示,在同一平面直角坐标系内,直线l :y= kx+b与直线 分别与x轴交于点(-2,0)与(5,0),则不等式组 的解为( ).
A. x<-2 B. x>5
C.-23.已知在平面直角坐标系xOy中,直线y=2x+2和直线 分别交x轴于点A 和点B,则下列直线中,与x轴的交点不在线段AB 上的直线是( ).
A. y=x+2
C. y=4x+2
4.设甲、乙两车在同一条笔直的公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x(s)后两车间的距离为y(m),y关于x的函数图象如图所示,则甲车的速度是( ).
A.25m/s B.20m/s C.45m/s D.15m/s
5.如图所示,一次函数. 的图象l 与 的图象 l 相交于点 P,则关于x的不等式 的解为 .
6.一个装有进水管和出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的部分关系图象如图所示.那么,从关闭进水管起 min,该容器内的水恰好放完.
7.一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a= .
8.已知一次函数y= kx+b与y= mx+n的图象如图所示.
(1)写出关于x,y的方程组 的解.
(2)若0< kx+b< mx+n,根据图象写出x的取值范围.
9.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段 DE 表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元.
(2)求y与x之间的函数表达式,并写出x的取值范围.
(3)日销售利润不低于640元的天数共有多少天 试销售期间,日销售最大利润是多少元
10.如图1所示为深50cm的圆柱形容器,底部放入一个长方体铁块,现在以一定的速度向容器内注水,图2为容器顶部离水面的距离 y(cm)随时间t(min)变化的函数图象,则( ).
A.注水的速度为每分钟注入 cm高水位的水
B.放入的长方体的高度为30cm
C.该容器注满水所用的时间为21min
D.此长方体的体积为此容器体积的
11.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=960;④a=34.以上结论中,正确的有( ).
A.①② B.①②③ C.①③④ D.①②④
12.【鞍山】如图所示,在平面直角坐标系中,点A ,A ,A ,A ,…在x轴正半轴上,点 B ,B ,B ,……在直线 上,若点 A (1,0),且△A B A ,△A B A ,△A B A ,…均为等边三角形,则线段 B B 的长度为( ).
13.小明在解方程组 的过程中错把b 看成了6,他其余的解题过程没有出错,解得此方程组的解为 又已知直线 y= kx+b过点(3,-1),则b的值是 .
14.甲、乙两车分别从A,B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达 B 地后马上以另一速度原路返回A 地(掉头的时间忽略不计),乙车到达 A 地以后即停在原地等待甲车.如图所示为甲、乙两车间的距离y(km)与甲车的行驶时间x(h)之间的函数图象,则当乙车到达A 地时,甲车与A 地之间的距离为 km.
15.如图1所示,水平放置的长方体容器的底面积为( ,其内部水平放置着一个实心长方体,长方体的底面积为20cm .现向容器内匀速注水,注满为止.在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示.
(1)匀速注水的水流速度为 cm /s.
(2)求长方体容器的高.
(3)求注水过程中水面高度h(cm)关于注水时间t(s)的函数表达式;并求注水多长时间,长方体容器内水面高度达到长方体容器高度的一半.
16.某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟,如图所示为两车离甲地的距离y(单位:km)与快递车所用时间x(单位:h)的函数图象,已知货车比快递车早1h出发,到达乙地后用2h装卸货物,按原速、原路返回,货车比快递车最后一次返回甲地晚1h.
(1)求 ME 的函数表达式.
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离乙地的距离.(直接写出答案)
17.甲、乙两动点分别从线段AB 的两端点同时出发,甲从点 A出发,向终点 B 运动,乙从点 B 出发,向终点 A 运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为 y(cm),y关于x的函数图象如图所示,则图中线段 DE所表示的函数表达式为 .(写出自变量的取值范围)
18.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y (元),且 按照方案二所需费用为 y (元),且 其函数图象如图所示.
(1)求k 和b的值,并说明它们的实际意义.
(2)求打折前的每次健身费用和k 的值.
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 请说明理由.
19.在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地.两车同时出发,匀速行驶,客车、货车离服务区的距离. 与行驶时间x(h)的函数关系图象如图1所示.
(1)甲、乙两地相距 km.
(2)求出发3h后,货车离服务区的距离y (km)与行驶时间x(h)之间的函数表达式.
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离y (km)与行驶时间x(h)之间的函数关系图象如图2中的虚线所示,经过多长时间邮政车与客车和货车的距离相等 请直接写出结果.
5.5 一次函数的简单应用(2)
1. B 2. A 3. C 4. B 5. x<-2 6.8 7.5
8.(1){x=y=3,4,(2)39.(1)340--(24-22)×5=330(件),330×(8-6)=660(元).故答案为:330,660.
(2)设线段OD所表示的y与x之间的函数表达式为y= kx,
将(17,340)代入 y= kx得340=17k,解得k=20.
∴线段OD所表示的y与x之间的函数表达式为y=20x.
根据题意得,线段 DE所表示的y与x之间的函数表达式为y=340-5(x-22)=-5x+450.
联立两线段所表示的函数表达式组成方程组得 解得
∴点 D 的坐标为(18,360).∴y与x之间的函数表达式为
(3)当0≤x≤18时,根据题意得(8-6)×20x≥640,解得x≥16.当18∴16≤x≤26.26-16+1=11(天),
∴日销售利润不低于 640元的天数共有11天.
∵点 D 的坐标为(18,360),
∴日最大销售量为360件.
360×(8-6)=720(元),
∴试销售期间,日销售最大利润是720元.
10. C 11. D 12. D 13.-13 14.630
15.(1)120
(2)设长方体容器的高度为 a(cm).
∴(a-30)×60=120×10,解得a=50.
∴长方体容器的高为50cm.
(3)当0当10∴水面高度 h 关于注水时间t 的函数表达式为
当水面高度达到长方体容器高度的一半时,h=25,∵30>25,∴25=3t,解得
∴注水 s时水面高度达到长方体容器高度的一半.
16.(1)设 ME的函数表达式为y= kx+b(k≠0),由 ME经过(0,50),(3,200)可得:
解得
∴ME的函数表达式为y=50x+50.
(2)设 BC的函数表达式为y= mx+n,由 BC经过(4,0),(6,200)可得:
解得
∴BC的函数表达式为y=100x-400.
设 FG 的函数表达式为 y= px+q,由 FG 经过(5,200),(9,0)可得:
解得
∴FG的函数表达式为y=-50x+450.
解方程组 得
设CD 的函数表达式为 y= cx+d,由 CD 经过(8,0),(6,200)可得:
解得
∴CD的函数表达式为y=-100x+800.
解方程组 得
∴快递车第二次往返过程中,与货车相遇的时间是 h或7h.
(3)(7-5)×50=100(km),
∴两车最后一次相遇时离乙地的距离为100km.
17. y=4.5x-90(20≤x≤36)
过点(0,30),(10,180), 解得
表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元;
b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),
则
(3)选择方案一所需费用更少.理由如下:
由题意可知,
当健身8次时,
选择方案一所需费用: (元);
选择方案二所需费用: )(元).
∵150<160,
∴选择方案一所需费用更少.
19.(1)360+120=480(km).故答案为:480.
(2)设3h后,货车离服务区的距离 y 与行驶时间x之间的函数关系式为
由图象可得,货车的速度为120÷3=40(km/h),则点 B 的横坐标为3+360÷40=12,
∴点 B 的坐标为(12,360).
由 得
即3h后,货车离服务区的距离y 与行驶时间x之间的函数关系式为
(3)v客=360÷6=60(km/h),υ邮=360×2÷8=90(km/h).
设当邮政车去甲地的途中时,经过t(h)邮政车与客车和货车的距离相等,
则120+(90-40)t=360--(60+90)t,解得 t=1.2.
设当邮政车从甲地返回乙地时,经过t(h)邮政车与客车和货车的距离相等,
则90t-360-(480-40t)=60t-(90t-360),解得t=7.5.
当客车和货车相遇时,邮政车与客车和货车的距离相等满足条件,即60t+40t=480,解得 t=4.8.
综上所述,经过1.2h或4.8h或7.5h,邮政车与客车和货车的距离相等.
5.5 一次函数的简单应用(2)
1.某商户以每件8元的价格购进若干件“四季如春植绒窗花”到市场去销售,销售金额y(元)与销售量x(件)之间的函数关系的图象如图所示,则降价后每件商品销售的价格为( ).
A.5元 B.10元 C.12.5元 D.15元
2.如图所示,在同一平面直角坐标系内,直线l :y= kx+b与直线 分别与x轴交于点(-2,0)与(5,0),则不等式组 的解为( ).
A. x<-2 B. x>5
C.-2
A. y=x+2
C. y=4x+2
4.设甲、乙两车在同一条笔直的公路上匀速行驶,开始甲车在乙车的前面,当乙车追上甲车后,两车停下来,把乙车的货物转给甲车,然后甲车继续前行,乙车原地返回.设x(s)后两车间的距离为y(m),y关于x的函数图象如图所示,则甲车的速度是( ).
A.25m/s B.20m/s C.45m/s D.15m/s
5.如图所示,一次函数. 的图象l 与 的图象 l 相交于点 P,则关于x的不等式 的解为 .
6.一个装有进水管和出水管的容器,从某时刻开始的4min内只进水不出水,在随后的8min内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的部分关系图象如图所示.那么,从关闭进水管起 min,该容器内的水恰好放完.
7.一辆货车从甲地匀速驶往乙地,到达后用了半小时卸货,随即匀速返回,已知货车返回的速度是它从甲地驶往乙地的速度的1.5倍.货车离甲地的距离y(km)关于时间x(h)的函数图象如图所示,则a= .
8.已知一次函数y= kx+b与y= mx+n的图象如图所示.
(1)写出关于x,y的方程组 的解.
(2)若0< kx+b< mx+n,根据图象写出x的取值范围.
9.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段 DE 表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元.
(2)求y与x之间的函数表达式,并写出x的取值范围.
(3)日销售利润不低于640元的天数共有多少天 试销售期间,日销售最大利润是多少元
10.如图1所示为深50cm的圆柱形容器,底部放入一个长方体铁块,现在以一定的速度向容器内注水,图2为容器顶部离水面的距离 y(cm)随时间t(min)变化的函数图象,则( ).
A.注水的速度为每分钟注入 cm高水位的水
B.放入的长方体的高度为30cm
C.该容器注满水所用的时间为21min
D.此长方体的体积为此容器体积的
11.甲、乙两人分别从A,B两地同时出发,相向而行,匀速前往B地、A地,两人相遇时停留了4min,又各自按原速前往目的地,甲、乙两人之间的距离y(m)与甲所用时间x(min)之间的函数关系如图所示.有下列说法:①A,B之间的距离为1200m;②乙行走的速度是甲的1.5倍;③b=960;④a=34.以上结论中,正确的有( ).
A.①② B.①②③ C.①③④ D.①②④
12.【鞍山】如图所示,在平面直角坐标系中,点A ,A ,A ,A ,…在x轴正半轴上,点 B ,B ,B ,……在直线 上,若点 A (1,0),且△A B A ,△A B A ,△A B A ,…均为等边三角形,则线段 B B 的长度为( ).
13.小明在解方程组 的过程中错把b 看成了6,他其余的解题过程没有出错,解得此方程组的解为 又已知直线 y= kx+b过点(3,-1),则b的值是 .
14.甲、乙两车分别从A,B两地同时出发,相向行驶,已知甲车的速度大于乙车的速度,甲车到达 B 地后马上以另一速度原路返回A 地(掉头的时间忽略不计),乙车到达 A 地以后即停在原地等待甲车.如图所示为甲、乙两车间的距离y(km)与甲车的行驶时间x(h)之间的函数图象,则当乙车到达A 地时,甲车与A 地之间的距离为 km.
15.如图1所示,水平放置的长方体容器的底面积为( ,其内部水平放置着一个实心长方体,长方体的底面积为20cm .现向容器内匀速注水,注满为止.在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图2所示.
(1)匀速注水的水流速度为 cm /s.
(2)求长方体容器的高.
(3)求注水过程中水面高度h(cm)关于注水时间t(s)的函数表达式;并求注水多长时间,长方体容器内水面高度达到长方体容器高度的一半.
16.某物流公司的快递车和货车每天往返于甲、乙两地,快递车比货车多往返一趟,如图所示为两车离甲地的距离y(单位:km)与快递车所用时间x(单位:h)的函数图象,已知货车比快递车早1h出发,到达乙地后用2h装卸货物,按原速、原路返回,货车比快递车最后一次返回甲地晚1h.
(1)求 ME 的函数表达式.
(2)求快递车第二次往返过程中,与货车相遇的时间.
(3)求两车最后一次相遇时离乙地的距离.(直接写出答案)
17.甲、乙两动点分别从线段AB 的两端点同时出发,甲从点 A出发,向终点 B 运动,乙从点 B 出发,向终点 A 运动.已知线段AB长为90cm,甲的速度为2.5cm/s.设运动时间为x(s),甲、乙两点之间的距离为 y(cm),y关于x的函数图象如图所示,则图中线段 DE所表示的函数表达式为 .(写出自变量的取值范围)
18.暑期将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:
方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠;
方案二:不购买学生暑期专享卡,每次健身费用按八折优惠.
设某学生暑期健身x(次),按照方案一所需费用为y (元),且 按照方案二所需费用为 y (元),且 其函数图象如图所示.
(1)求k 和b的值,并说明它们的实际意义.
(2)求打折前的每次健身费用和k 的值.
(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少 请说明理由.
19.在甲、乙两城市之间有一服务区,一辆客车从甲地驶往乙地,一辆货车从乙地驶往甲地.两车同时出发,匀速行驶,客车、货车离服务区的距离. 与行驶时间x(h)的函数关系图象如图1所示.
(1)甲、乙两地相距 km.
(2)求出发3h后,货车离服务区的距离y (km)与行驶时间x(h)之间的函数表达式.
(3)在客车和货车出发的同时,有一辆邮政车从服务区匀速去甲地取货后返回乙地(取货的时间忽略不计),邮政车离服务区的距离y (km)与行驶时间x(h)之间的函数关系图象如图2中的虚线所示,经过多长时间邮政车与客车和货车的距离相等 请直接写出结果.
5.5 一次函数的简单应用(2)
1. B 2. A 3. C 4. B 5. x<-2 6.8 7.5
8.(1){x=y=3,4,(2)3
(2)设线段OD所表示的y与x之间的函数表达式为y= kx,
将(17,340)代入 y= kx得340=17k,解得k=20.
∴线段OD所表示的y与x之间的函数表达式为y=20x.
根据题意得,线段 DE所表示的y与x之间的函数表达式为y=340-5(x-22)=-5x+450.
联立两线段所表示的函数表达式组成方程组得 解得
∴点 D 的坐标为(18,360).∴y与x之间的函数表达式为
(3)当0≤x≤18时,根据题意得(8-6)×20x≥640,解得x≥16.当18
∴日销售利润不低于 640元的天数共有11天.
∵点 D 的坐标为(18,360),
∴日最大销售量为360件.
360×(8-6)=720(元),
∴试销售期间,日销售最大利润是720元.
10. C 11. D 12. D 13.-13 14.630
15.(1)120
(2)设长方体容器的高度为 a(cm).
∴(a-30)×60=120×10,解得a=50.
∴长方体容器的高为50cm.
(3)当0
当水面高度达到长方体容器高度的一半时,h=25,∵30>25,∴25=3t,解得
∴注水 s时水面高度达到长方体容器高度的一半.
16.(1)设 ME的函数表达式为y= kx+b(k≠0),由 ME经过(0,50),(3,200)可得:
解得
∴ME的函数表达式为y=50x+50.
(2)设 BC的函数表达式为y= mx+n,由 BC经过(4,0),(6,200)可得:
解得
∴BC的函数表达式为y=100x-400.
设 FG 的函数表达式为 y= px+q,由 FG 经过(5,200),(9,0)可得:
解得
∴FG的函数表达式为y=-50x+450.
解方程组 得
设CD 的函数表达式为 y= cx+d,由 CD 经过(8,0),(6,200)可得:
解得
∴CD的函数表达式为y=-100x+800.
解方程组 得
∴快递车第二次往返过程中,与货车相遇的时间是 h或7h.
(3)(7-5)×50=100(km),
∴两车最后一次相遇时离乙地的距离为100km.
17. y=4.5x-90(20≤x≤36)
过点(0,30),(10,180), 解得
表示的实际意义是:购买一张学生暑期专享卡后每次健身费用为15元;
b=30表示的实际意义是:购买一张学生暑期专享卡的费用为30元.
(2)由题意可得,打折前的每次健身费用为15÷0.6=25(元),
则
(3)选择方案一所需费用更少.理由如下:
由题意可知,
当健身8次时,
选择方案一所需费用: (元);
选择方案二所需费用: )(元).
∵150<160,
∴选择方案一所需费用更少.
19.(1)360+120=480(km).故答案为:480.
(2)设3h后,货车离服务区的距离 y 与行驶时间x之间的函数关系式为
由图象可得,货车的速度为120÷3=40(km/h),则点 B 的横坐标为3+360÷40=12,
∴点 B 的坐标为(12,360).
由 得
即3h后,货车离服务区的距离y 与行驶时间x之间的函数关系式为
(3)v客=360÷6=60(km/h),υ邮=360×2÷8=90(km/h).
设当邮政车去甲地的途中时,经过t(h)邮政车与客车和货车的距离相等,
则120+(90-40)t=360--(60+90)t,解得 t=1.2.
设当邮政车从甲地返回乙地时,经过t(h)邮政车与客车和货车的距离相等,
则90t-360-(480-40t)=60t-(90t-360),解得t=7.5.
当客车和货车相遇时,邮政车与客车和货车的距离相等满足条件,即60t+40t=480,解得 t=4.8.
综上所述,经过1.2h或4.8h或7.5h,邮政车与客车和货车的距离相等.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
