4.1 列代数式 提优训练(含答案)
文档属性
| 名称 | 4.1 列代数式 提优训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 228.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-26 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.1 列代数式
1. “x与3的差的2 倍”用代数式表示为( ).
A.2x-3 B.2(x-3) C.3(x-2) D.3x-2
2.式子a+b,S= ab,5,m,8+y,m+3=2中,代数式有( ).
A.6个 B.5个 C.4个 D.3个
3.下列叙述中错误的是( ).
A.比a的2倍大1的数是2a+1 B. a的相反数与b的和是-a+b
C.比a的平方小1的数是 D. a的2倍与b的差的3倍是2a-3b
4.用代数式表示“a的5倍与b的 的差”是 .
5.某影院针对一部影片推出了特惠活动:票价每人30元,团体购票超过10人,票价可享受八折优惠.学校计划组织全体教师观看此影片,若观影人数为a(a>10),则应付票价总额为 元(用含a的式子表示).
6.将三个连续的自然数由小到大排列,若中间的一个为n,则第一个为 ,第三个为
7.用代数式表示:
(1)某商品售价为a元,打八折后又降价20元,则现价为 元.
(2)如图所示,图1需4根火柴,图2需 根火柴,图3需 根火柴……图n需 根火柴.
8.用代数式表示:
(1)比a与b的积的2倍小5的数.
(2)a 与b 的平方差.
(3)被5除商是 a,余数是2的数.
9.一个两位数,个位上是x,十位上是y,用代数式表示这个两位数是( ).
A. xy B. yx C.10x+y D.10y+x
10.代数式 的正确解释是( ).
A. a与b 的倒数的差的平方 B. a与b的差的平方的倒数
C. a的平方与b的差的倒数 D. a的平方与b 的倒数的差
11.销售一种礼服和围巾,礼服每套标价800元,围巾每条标价120元,近期商场决定开展促销活动,活动期间向客户提供的优惠方案是买一套礼服送一条围巾.现某客户到该商场买礼服20套,围巾a条(a>20),则需付款 元.
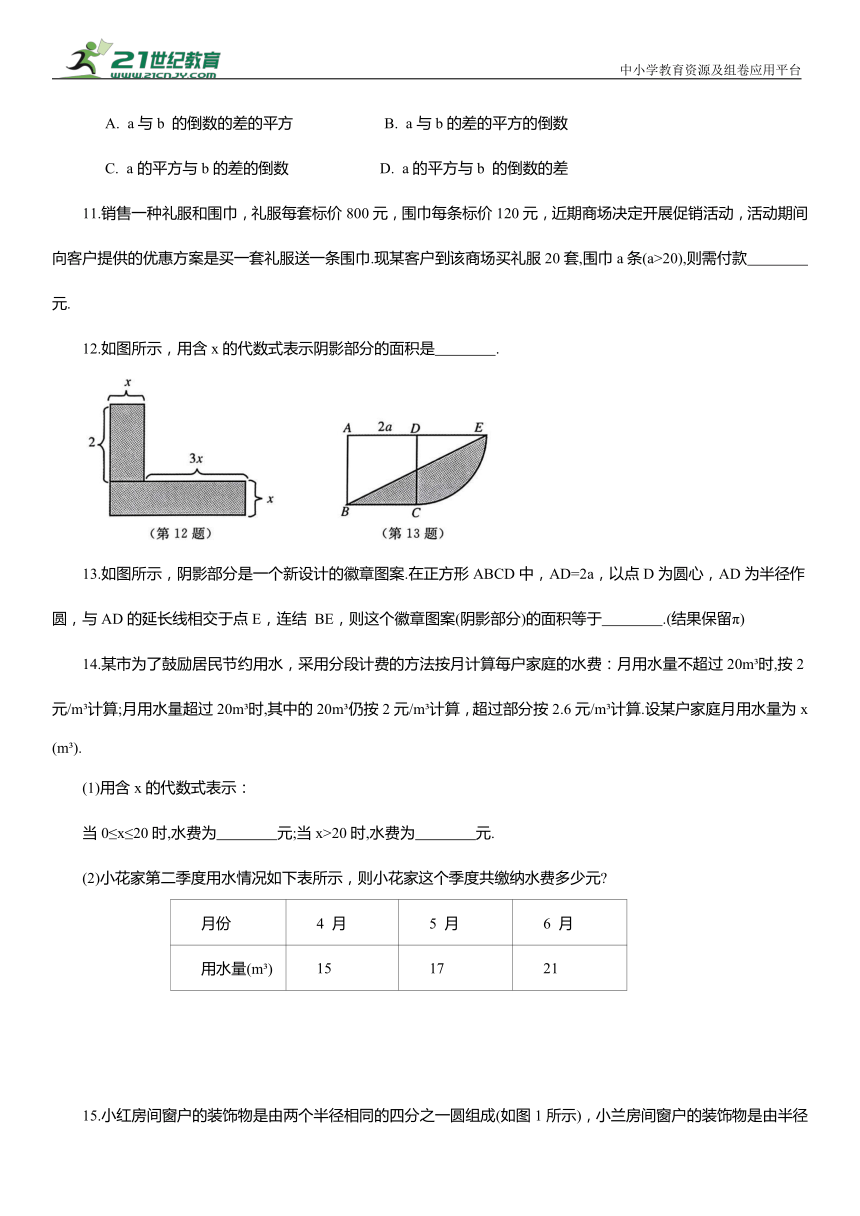
12.如图所示,用含x的代数式表示阴影部分的面积是 .
13.如图所示,阴影部分是一个新设计的徽章图案.在正方形ABCD中,AD=2a,以点D为圆心,AD为半径作圆,与AD的延长线相交于点E,连结 BE,则这个徽章图案(阴影部分)的面积等于 .(结果保留π)
14.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费:月用水量不超过20m 时,按2元/m 计算;月用水量超过20m 时,其中的20m 仍按2元/m 计算,超过部分按2.6元/m 计算.设某户家庭月用水量为x(m ).
(1)用含x的代数式表示:
当0≤x≤20时,水费为 元;当x>20时,水费为 元.
(2)小花家第二季度用水情况如下表所示,则小花家这个季度共缴纳水费多少元
月份 4 月 5 月 6 月
用水量(m ) 15 17 21
15.小红房间窗户的装饰物是由两个半径相同的四分之一圆组成(如图1所示),小兰房间窗户的装饰物是由半径相同的两个四分之一圆和一个半圆组成(如图2所示),小明房间窗户的装饰物是由半径相同的两个四分之一圆和两个半圆组成(如图3所示).
(1)根据装饰物图案变化的规律,设计下一个装饰物图案.
(2)分别求出图1,图2,图3中装饰物所占的面积(结果要求化简).
(3)你能发现装饰物面积变化的规律吗 请用代数式表示出第n个装饰物的面积.
16.如图所示,将边长为3a 的正方形沿虚线剪成两个正方形和两个长方形.若拿掉边长为2b的小正方形后,再将剩下的三块拼成一个长方形,则这个长方形的长为( ).
A.3a+2b B.3a+4b
C.6a+2b D.6a+4b
17.某国家森林公园门票的价格为成人票每张30元,儿童票每张15 元.若购买m张成人票和n张儿童票,则共需花费 元.
18.用如图所示的曲尺形框(有三个方向),可以套住下表中的三个数,设被框住的三个数中最小的数为a.
(1)用含a的式子分别表示出被不同方向的曲尺形框框出的这三个数的和.
(2)若这三个数的和是48,求a的值.
1. B 2. C 3. D 4.5a- b 5.24a
6. n-1 n+1 7.(1)(0.8a-20) (2)7 10 (3n+1)
8.(1)2ab--5. (2)a -b . (3)5a+2.
9. D 10. D 11.(120a+13600) 12.4x +2x
13.πa
14.(1)2x 2.6x--12
(2)15×2+17×2+2.6×21-12
=30+34+54.6-12
=106.6(元).
∴小花家这个季度共缴纳水费106.6元.
15.(1)下一个装饰物图案是半径相同的两个四分之一圆和三个半圆.
(2)图1中装饰物所占的面积是 图2中装饰物所占的面积是
图 3 中 装 饰 物 所 占 的 面积是
(3)第n个装饰物的面积是π/8b (n为正整数).
16. A 17.(30m+15n)
18.(1)设被第一个框框住的三个数中最小的数为a,则a+a+1+a+7=3a+8;
设被第二个框框住的三个数中最小的数为a,则a+a+7+a+8=3a+15;
设被第三个框框住的三个数中最小的数为a,则a+a+1+a+8=3a+9.
(2)设被第一个框框住的三个数的和是48,则3a+8=48,解得 显然不符合题意;设被第二个框框住的三个数的和是48,则3a+15=48,解得a=11,符合题意;设被第三个框框住的三个数的和是48,则3a+9=48,解得a=13,符合题意.综上所述,a的值为11或13.
4.1 列代数式
1. “x与3的差的2 倍”用代数式表示为( ).
A.2x-3 B.2(x-3) C.3(x-2) D.3x-2
2.式子a+b,S= ab,5,m,8+y,m+3=2中,代数式有( ).
A.6个 B.5个 C.4个 D.3个
3.下列叙述中错误的是( ).
A.比a的2倍大1的数是2a+1 B. a的相反数与b的和是-a+b
C.比a的平方小1的数是 D. a的2倍与b的差的3倍是2a-3b
4.用代数式表示“a的5倍与b的 的差”是 .
5.某影院针对一部影片推出了特惠活动:票价每人30元,团体购票超过10人,票价可享受八折优惠.学校计划组织全体教师观看此影片,若观影人数为a(a>10),则应付票价总额为 元(用含a的式子表示).
6.将三个连续的自然数由小到大排列,若中间的一个为n,则第一个为 ,第三个为
7.用代数式表示:
(1)某商品售价为a元,打八折后又降价20元,则现价为 元.
(2)如图所示,图1需4根火柴,图2需 根火柴,图3需 根火柴……图n需 根火柴.
8.用代数式表示:
(1)比a与b的积的2倍小5的数.
(2)a 与b 的平方差.
(3)被5除商是 a,余数是2的数.
9.一个两位数,个位上是x,十位上是y,用代数式表示这个两位数是( ).
A. xy B. yx C.10x+y D.10y+x
10.代数式 的正确解释是( ).
A. a与b 的倒数的差的平方 B. a与b的差的平方的倒数
C. a的平方与b的差的倒数 D. a的平方与b 的倒数的差
11.销售一种礼服和围巾,礼服每套标价800元,围巾每条标价120元,近期商场决定开展促销活动,活动期间向客户提供的优惠方案是买一套礼服送一条围巾.现某客户到该商场买礼服20套,围巾a条(a>20),则需付款 元.
12.如图所示,用含x的代数式表示阴影部分的面积是 .
13.如图所示,阴影部分是一个新设计的徽章图案.在正方形ABCD中,AD=2a,以点D为圆心,AD为半径作圆,与AD的延长线相交于点E,连结 BE,则这个徽章图案(阴影部分)的面积等于 .(结果保留π)
14.某市为了鼓励居民节约用水,采用分段计费的方法按月计算每户家庭的水费:月用水量不超过20m 时,按2元/m 计算;月用水量超过20m 时,其中的20m 仍按2元/m 计算,超过部分按2.6元/m 计算.设某户家庭月用水量为x(m ).
(1)用含x的代数式表示:
当0≤x≤20时,水费为 元;当x>20时,水费为 元.
(2)小花家第二季度用水情况如下表所示,则小花家这个季度共缴纳水费多少元
月份 4 月 5 月 6 月
用水量(m ) 15 17 21
15.小红房间窗户的装饰物是由两个半径相同的四分之一圆组成(如图1所示),小兰房间窗户的装饰物是由半径相同的两个四分之一圆和一个半圆组成(如图2所示),小明房间窗户的装饰物是由半径相同的两个四分之一圆和两个半圆组成(如图3所示).
(1)根据装饰物图案变化的规律,设计下一个装饰物图案.
(2)分别求出图1,图2,图3中装饰物所占的面积(结果要求化简).
(3)你能发现装饰物面积变化的规律吗 请用代数式表示出第n个装饰物的面积.
16.如图所示,将边长为3a 的正方形沿虚线剪成两个正方形和两个长方形.若拿掉边长为2b的小正方形后,再将剩下的三块拼成一个长方形,则这个长方形的长为( ).
A.3a+2b B.3a+4b
C.6a+2b D.6a+4b
17.某国家森林公园门票的价格为成人票每张30元,儿童票每张15 元.若购买m张成人票和n张儿童票,则共需花费 元.
18.用如图所示的曲尺形框(有三个方向),可以套住下表中的三个数,设被框住的三个数中最小的数为a.
(1)用含a的式子分别表示出被不同方向的曲尺形框框出的这三个数的和.
(2)若这三个数的和是48,求a的值.
1. B 2. C 3. D 4.5a- b 5.24a
6. n-1 n+1 7.(1)(0.8a-20) (2)7 10 (3n+1)
8.(1)2ab--5. (2)a -b . (3)5a+2.
9. D 10. D 11.(120a+13600) 12.4x +2x
13.πa
14.(1)2x 2.6x--12
(2)15×2+17×2+2.6×21-12
=30+34+54.6-12
=106.6(元).
∴小花家这个季度共缴纳水费106.6元.
15.(1)下一个装饰物图案是半径相同的两个四分之一圆和三个半圆.
(2)图1中装饰物所占的面积是 图2中装饰物所占的面积是
图 3 中 装 饰 物 所 占 的 面积是
(3)第n个装饰物的面积是π/8b (n为正整数).
16. A 17.(30m+15n)
18.(1)设被第一个框框住的三个数中最小的数为a,则a+a+1+a+7=3a+8;
设被第二个框框住的三个数中最小的数为a,则a+a+7+a+8=3a+15;
设被第三个框框住的三个数中最小的数为a,则a+a+1+a+8=3a+9.
(2)设被第一个框框住的三个数的和是48,则3a+8=48,解得 显然不符合题意;设被第二个框框住的三个数的和是48,则3a+15=48,解得a=11,符合题意;设被第三个框框住的三个数的和是48,则3a+9=48,解得a=13,符合题意.综上所述,a的值为11或13.
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
