专题复习二 与角度有关的计算 提优训练(含答案)
文档属性
| 名称 | 专题复习二 与角度有关的计算 提优训练(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 287.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-27 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题复习二 与角度有关的计算
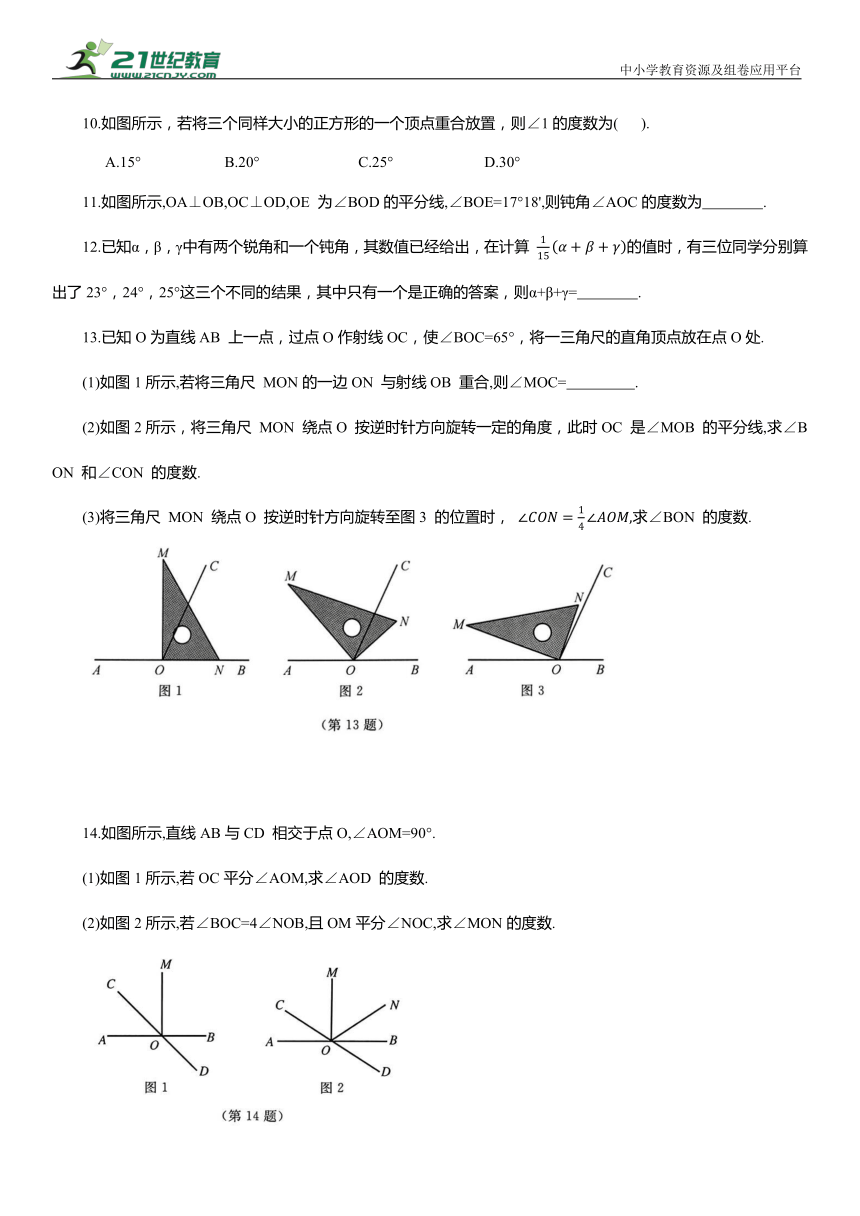
1.如图所示,OA 是北偏东30°方向上的一条射线,若射线OB 与射线OA 垂直,则射线 OB 的方位角是( ).
A.北偏西30° B.北偏西60° C.东偏北 30° D.东偏北60°
2.如图所示,OB是∠AOC 的平分线,OD 是∠COE 的平分线,如果∠AOB=40°,∠COE=60°,那么∠BOD 的度数为( ).
A.50° B.60° C.65° D.70°
3.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON 的度数为( ).
A.35° B.45° C.55° D.65°
4.如图所示,直线 AB,CD 相交于点O,OM⊥AB 于点O.若∠MOD=43°,则∠COB= 度.
5.若一个角的余角比这个角的补角的一半小40°,则这个角为 度.
6.如图所示,AO⊥OC,射线OC 平分∠DOB,∠DOC=20°,则∠AOB=
7.在直线AB上任意取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD= .
8.如图所示,∠AOB=∠COD=90°.
(1)∠AOC等于∠BOD 吗 请说明理由.
(2)若∠BOD=136°,则∠BOC 等于多少度
9.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠MOC=35°,则∠BON 的度数为( ).
A.35° B.45° C.55° D.64°
10.如图所示,若将三个同样大小的正方形的一个顶点重合放置,则∠1的度数为( ).
A.15° B.20° C.25° D.30°
11.如图所示,OA⊥OB,OC⊥OD,OE 为∠BOD的平分线,∠BOE=17°18',则钝角∠AOC的度数为 .
12.已知α,β,γ中有两个锐角和一个钝角,其数值已经给出,在计算 的值时,有三位同学分别算出了23°,24°,25°这三个不同的结果,其中只有一个是正确的答案,则α+β+γ= .
13.已知O为直线AB 上一点,过点O作射线OC,使∠BOC=65°,将一三角尺的直角顶点放在点O处.
(1)如图1所示,若将三角尺 MON的一边ON 与射线OB 重合,则∠MOC= .
(2)如图2所示,将三角尺 MON 绕点O 按逆时针方向旋转一定的角度,此时OC 是∠MOB 的平分线,求∠BON 和∠CON 的度数.
(3)将三角尺 MON 绕点O 按逆时针方向旋转至图3 的位置时, 求∠BON 的度数.
14.如图所示,直线AB与CD 相交于点O,∠AOM=90°.
(1)如图1所示,若OC平分∠AOM,求∠AOD 的度数.
(2)如图2所示,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
15.已知M,N,P,Q四点的位置如图所示,下列结论中正确的是( ).
A.∠NOQ=42° B.∠NOP=132°
C.∠PON 比∠MOQ 大 D.∠MOQ 与∠MOP 互补
16.如图所示,已知∠AOB 是直角,∠AOC是锐角,ON 平分∠AOC,OM平分∠BOC,则∠MON 是( ).
A.45° D.无法计算
7.如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).
(1)如图1所示,O为直线AB 上一点,OC⊥AB于点O,OE⊥OD 于点O,直接指出图中所有互为垂角的角.
(2)若一个角的垂角等于这个角的补角的 ,求这个角的度数.
(3)如图2所示,O为直线AB 上一点,∠AOC=75°,将整个图形绕点O按逆时针方向旋转n°(0专题复习二 与角度有关的计算
1. B 2. D 3. C 4.133 5.80 6.70°
7.60°或120°
8.(1)∠AOC=∠BOD.∵∠AOB=∠COD=90°,∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD.
(2)∵∠BOD+∠COD+∠BOC=360°,即136°+90°+∠BOC=360°,∴∠BOC=134°.
9. C 10. B 11.145°24′ 12.345°
13.(1)25°
(2)∵∠BOC=65°,OC 是∠MOB 的平分线,∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB-∠MON=130°-90°=40°,
∠CON=∠BOC--∠BON=65°-40°=25°.
∵∠BOC=65°,∴∠AOC=180°-65°=115°.
∵∠MON=90°,∴∠AOM+∠CON=∠AOC-∠MON=115°-90°=25°.
∴4∠CON+∠CON=25°.∴∠CON=5°.
∴∠BON=∠CON+∠BOC=70°.
14.(1)∵∠AOM=90°,OC平分∠AOM,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°.
(2)∵∠BOC=4∠NOB,
∴设∠NOB=x°,则∠BOC=4x°.
∴∠CON=∠COB-∠BON=4x°-x°=3x°.
∵OM平分∠CON,
解得x=36.
15. C 16. A
17.(1)互为垂角的角有 4 对:∠EOB 与∠DOB,∠EOB 与∠EOC,∠AOD 与∠COD,∠AOD 与∠AOE.
(2)设这个角的度数为x°,则
①当0②当90综上所述,这个角的度数为 18°或126°.
(3)当n=75时OC'和OA 重合,分两种情况:
①当0∠A'OP=180°-(∠POB+∠BOB')=180°-2n°,
∵∠A'OP 与∠AOC'互为垂角,
∴|(180-2n)-(75-n)|=90,解得n=15或195.
∵0②当75∵∠A'OP 与∠AOC'互为垂直,
∴|(180-2n)-(n-75)|=90,解得n=55或115.
∵75综上所述,当n=15 时,∠A'OP 与∠AOC'互为垂角.
专题复习二 与角度有关的计算
1.如图所示,OA 是北偏东30°方向上的一条射线,若射线OB 与射线OA 垂直,则射线 OB 的方位角是( ).
A.北偏西30° B.北偏西60° C.东偏北 30° D.东偏北60°
2.如图所示,OB是∠AOC 的平分线,OD 是∠COE 的平分线,如果∠AOB=40°,∠COE=60°,那么∠BOD 的度数为( ).
A.50° B.60° C.65° D.70°
3.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON 的度数为( ).
A.35° B.45° C.55° D.65°
4.如图所示,直线 AB,CD 相交于点O,OM⊥AB 于点O.若∠MOD=43°,则∠COB= 度.
5.若一个角的余角比这个角的补角的一半小40°,则这个角为 度.
6.如图所示,AO⊥OC,射线OC 平分∠DOB,∠DOC=20°,则∠AOB=
7.在直线AB上任意取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD= .
8.如图所示,∠AOB=∠COD=90°.
(1)∠AOC等于∠BOD 吗 请说明理由.
(2)若∠BOD=136°,则∠BOC 等于多少度
9.如图所示,直线AB,CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠MOC=35°,则∠BON 的度数为( ).
A.35° B.45° C.55° D.64°
10.如图所示,若将三个同样大小的正方形的一个顶点重合放置,则∠1的度数为( ).
A.15° B.20° C.25° D.30°
11.如图所示,OA⊥OB,OC⊥OD,OE 为∠BOD的平分线,∠BOE=17°18',则钝角∠AOC的度数为 .
12.已知α,β,γ中有两个锐角和一个钝角,其数值已经给出,在计算 的值时,有三位同学分别算出了23°,24°,25°这三个不同的结果,其中只有一个是正确的答案,则α+β+γ= .
13.已知O为直线AB 上一点,过点O作射线OC,使∠BOC=65°,将一三角尺的直角顶点放在点O处.
(1)如图1所示,若将三角尺 MON的一边ON 与射线OB 重合,则∠MOC= .
(2)如图2所示,将三角尺 MON 绕点O 按逆时针方向旋转一定的角度,此时OC 是∠MOB 的平分线,求∠BON 和∠CON 的度数.
(3)将三角尺 MON 绕点O 按逆时针方向旋转至图3 的位置时, 求∠BON 的度数.
14.如图所示,直线AB与CD 相交于点O,∠AOM=90°.
(1)如图1所示,若OC平分∠AOM,求∠AOD 的度数.
(2)如图2所示,若∠BOC=4∠NOB,且OM平分∠NOC,求∠MON的度数.
15.已知M,N,P,Q四点的位置如图所示,下列结论中正确的是( ).
A.∠NOQ=42° B.∠NOP=132°
C.∠PON 比∠MOQ 大 D.∠MOQ 与∠MOP 互补
16.如图所示,已知∠AOB 是直角,∠AOC是锐角,ON 平分∠AOC,OM平分∠BOC,则∠MON 是( ).
A.45° D.无法计算
7.如果两个角的差的绝对值等于90°,就称这两个角互为垂角,例如:∠1=120°,∠2=30°,|∠1-∠2|=90°,则∠1和∠2互为垂角(本题中所有角都是指大于0°且小于180°的角).
(1)如图1所示,O为直线AB 上一点,OC⊥AB于点O,OE⊥OD 于点O,直接指出图中所有互为垂角的角.
(2)若一个角的垂角等于这个角的补角的 ,求这个角的度数.
(3)如图2所示,O为直线AB 上一点,∠AOC=75°,将整个图形绕点O按逆时针方向旋转n°(0
1. B 2. D 3. C 4.133 5.80 6.70°
7.60°或120°
8.(1)∠AOC=∠BOD.∵∠AOB=∠COD=90°,∴∠AOB+∠AOD=∠COD+∠AOD,即∠AOC=∠BOD.
(2)∵∠BOD+∠COD+∠BOC=360°,即136°+90°+∠BOC=360°,∴∠BOC=134°.
9. C 10. B 11.145°24′ 12.345°
13.(1)25°
(2)∵∠BOC=65°,OC 是∠MOB 的平分线,∴∠MOB=2∠BOC=130°.
∴∠BON=∠MOB-∠MON=130°-90°=40°,
∠CON=∠BOC--∠BON=65°-40°=25°.
∵∠BOC=65°,∴∠AOC=180°-65°=115°.
∵∠MON=90°,∴∠AOM+∠CON=∠AOC-∠MON=115°-90°=25°.
∴4∠CON+∠CON=25°.∴∠CON=5°.
∴∠BON=∠CON+∠BOC=70°.
14.(1)∵∠AOM=90°,OC平分∠AOM,
∵∠AOC+∠AOD=180°,
∴∠AOD=180°-∠AOC=180°-45°=135°.
(2)∵∠BOC=4∠NOB,
∴设∠NOB=x°,则∠BOC=4x°.
∴∠CON=∠COB-∠BON=4x°-x°=3x°.
∵OM平分∠CON,
解得x=36.
15. C 16. A
17.(1)互为垂角的角有 4 对:∠EOB 与∠DOB,∠EOB 与∠EOC,∠AOD 与∠COD,∠AOD 与∠AOE.
(2)设这个角的度数为x°,则
①当0
(3)当n=75时OC'和OA 重合,分两种情况:
①当0
∵∠A'OP 与∠AOC'互为垂角,
∴|(180-2n)-(75-n)|=90,解得n=15或195.
∵0
∴|(180-2n)-(n-75)|=90,解得n=55或115.
∵75
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
