专题复习二 二次函数图象与系数的关系 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 专题复习二 二次函数图象与系数的关系 提优训练(含答案)2024-2025学年浙教版九年级数学上册 | 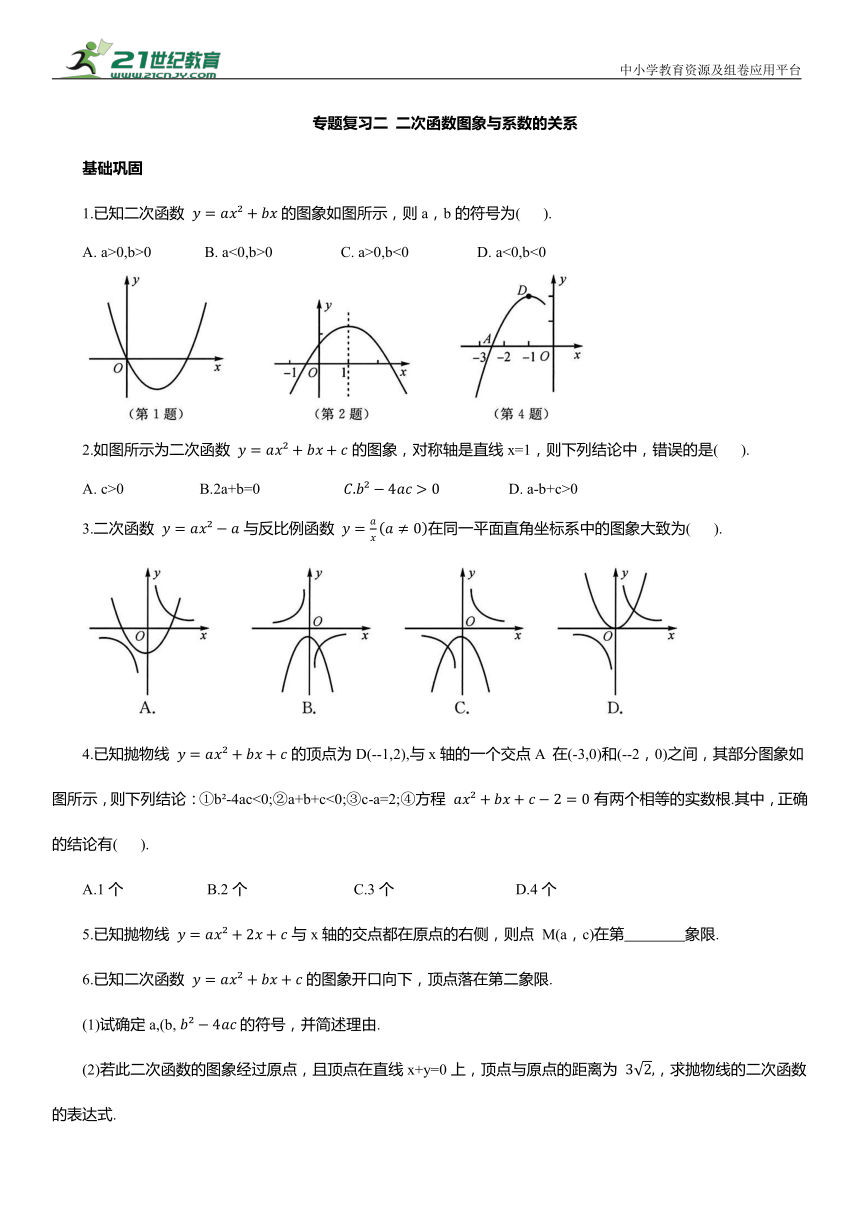 | |
| 格式 | docx | ||
| 文件大小 | 294.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 05:20:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题复习二 二次函数图象与系数的关系
基础巩固
1.已知二次函数 的图象如图所示,则a,b的符号为( ).
A. a>0,b>0 B. a<0,b>0 C. a>0,b<0 D. a<0,b<0
2.如图所示为二次函数 的图象,对称轴是直线x=1,则下列结论中,错误的是( ).
A. c>0 B.2a+b=0 D. a-b+c>0
3.二次函数 与反比例函数 在同一平面直角坐标系中的图象大致为( ).
4.已知抛物线 的顶点为D(--1,2),与x轴的一个交点A 在(-3,0)和(--2,0)之间,其部分图象如图所示,则下列结论:①b -4ac<0;②a+b+c<0;③c-a=2;④方程 有两个相等的实数根.其中,正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
5.已知抛物线 与x轴的交点都在原点的右侧,则点 M(a,c)在第 象限.
6.已知二次函数 的图象开口向下,顶点落在第二象限.
(1)试确定a,(b, 的符号,并简述理由.
(2)若此二次函数的图象经过原点,且顶点在直线x+y=0上,顶点与原点的距离为 ,求抛物线的二次函数的表达式.
7.已知函数 的顶点为点D.
(1)求点 D 的坐标(用含 m 的代数式表示).
(2)求函数 的图象与x轴的交点坐标.
(3)若函数 的图象在直线y=m的上方,求m的取值范围.
能力提升
8.已知抛物线 a是常数且a<0,下列选项中,可能为它的大致图象的是( ).
9.二次函数 的图象如图所示,现有下列结论:①4ac-b <0;②4a+c<2b;③3b+2c<0;④m(am+b)+bA.4个 B.3个
C.2个 D.1个
10.二次函数 的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t的取值范围是 .
11.已知二次函数 的图象如图所示,则 的值为 ,c/a的取值范围是 .
12.如图所示为抛物线 的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则a,b之间满足的关系式为 .
13.对于二次函数 如果当x取任意整数时,函数值y都是整数,那么我们把该函数的图象叫做“整点抛物线”(例如:
(1)请你写出一个二次项系数的绝对值小于1的“整点抛物线”的函数表达式: .(不必证明)
(2)请探索:是否存在二次项系数的绝对值小于 的“整点抛物线” 若存在,请写出其中一条抛物线的表达式;若不存在,请说明理由.
夯实演练
14.已知二次函数 图象的对称轴为直线x=1,其图象如图所示,现有下列结论:①abc>0;②b-2a<0;③a-b+c>0;④a+b>n(an+b)(n≠1);⑤2c<3b.其中,正确的是( ).
A.①③ B.②⑤
C.③④ D.④⑤
15.在平面直角坐标系中,设二次函数 其中a≠0.
(1)若函数 y1 的图象经过点(1,-2),求函数 y1的表达式.
(2)若一次函数 的图象与y2的图象经过x轴上的同一点,探究实数a,b满足的表达式.
(3)已知点 P(x1,m)和点 Q(1,n)在函数 y1的图象上,若 求x1的取值范围.
16.如图所示,二次函数 图象的顶点为 H,与x轴交于A,B两点(点 B在点A 右侧),点 H,B关于直线l: 对称.
(1)求A,B两点的坐标,并证明点 A 在直线l上.
(2)求二次函数的表达式.
(3)过点 B作直线. 交直线l于点K. M,N分别为直线AH 和直线l上的两个动点,连结 HN,NM,MK,求 的最小值.
专题复习二 二次函数图象与系数的关系
1. C 2. D 3. A 4. C 5.三
6.(1)∵抛物线开口向下,∴a<0.
∵顶点在第二象限,
(2)由题意可得c=0,此时顶点坐标为
∵顶点在直线x+y=0上, 此时顶点坐标为
或 (舍去).
∴抛物线的函数表达式为
∴顶点 D(m,-m ).
(2)令 y=0,得 解得
∴函数的图象与x轴的交点坐标为(0,0),(2m,0).
(3)∵函数 的图象在直线y=m的上方,
∴顶点 D 在直线y=m的上方.
即
∴m的取值范围是-18. B 9. B 10.0【解析】∵抛物线的对称轴为直线x=1,
即
由图象知当x=-2时,y>0,即4a-2b+c>0①,
当x=-1时,y<0,即a-b+c<0②,
将b=-2a代入①②,得c>-8a,c<-3a.
又
12. a-b+1=0
(2)假设存在符合条件的抛物线,则对于抛物线 bx+c,
当x=0时,y=c;当x=1时,y=a+b+c.
由整点抛物线定义知:c为整数,a+b+c为整数,∴a+b必为整数.
当x=2时,y=4a+2b+c=2a+2(a+b)+c是整数,∴2a必为整数.
∴不存在二次项系数的绝对值小于 的“整点抛物线”.
14. D 【解析】①由图象可知a<0,b>0,c>0, abc<0,故①错误.
②由于a<0,所以-2a>0.又b>0,所以b-2a>0,故②错误.
③当x=-1时,y=a-b+c<0,故③错误.
④当x=1时,y的值最大,此时y=a+b+c.
而当x=n时,
故 ,即a+b>n(an+b),故④正确.
⑤当x=3时函数值小于0,y=9a+3b+c<0,且该抛物线对称轴是直线 即 代入得 得2c<3b,故⑤正确.
故④⑤正确.故选 D.
15.(1)由函数y 的图象经过点(1,-2),
得(a+1)(-a)=-2,解得(
当 时,
当 时,
综上所述,函数y 的表达式为
(2)当y=0时,(x+a)(x-a-1)=0,解得. =a+1.
∴y 的图象与x轴的交点是(-a,0),(a+1,0).
当 经过(-a,0)时, 即 当y = ax+b经过(a+1,0)时, 即
(3)由题意知,函数 y 的对称轴为直线
当点 P 在对称轴的左侧(含顶点)时,y随x 的增大而减小,
(1,n)与(0,n)关于对称轴对称,
由 m当点 P 在对称轴的右侧时,y随x的增大而增大,由 m综上所述,m16.(1)由题意得ax +2ax-3a=0(a≠0),解得 x =
∴点 A 的坐标为(-3,0),点 B 的坐标为(1,0).
∵直线
当x=-3时
∴点A 在直线l上.
(2)∵点 H,B关于过点A 的直线 对称,∴AH=AB=4.
∵AH=BH,∴△ABH为正三角形.
如答图1所示,过顶点 H 作 HC⊥AB 于点C,则 AC=
∴顶点 H(-1,2 ),代入二次函数表达式,解得 a
∴二次函数表达式为
(3)易求得直线AH的函数表达式为 直线BK 的函数表达式为
日 解得
即 K(3,2 ).∴BK=4.
∵点 H,B关于直线AK 对称,
∴HN+MN的最小值是MB.
如答图2 所示,过点 K 作直线 AH 的对称点 Q,连结QK,交直线AH于点E,
则QM=MK,QE=EK=KD=2 ,则 AE⊥QK.
∴BM+MK 的最小值是BQ,即 BQ的长是HN+NM+MK 的最小值.
∵BK∥AH,∴∠BKQ=∠HEQ=90°.
由勾股定理可求得 QB=8.
∴HN+NM+MK 和的最小值为8.
专题复习二 二次函数图象与系数的关系
基础巩固
1.已知二次函数 的图象如图所示,则a,b的符号为( ).
A. a>0,b>0 B. a<0,b>0 C. a>0,b<0 D. a<0,b<0
2.如图所示为二次函数 的图象,对称轴是直线x=1,则下列结论中,错误的是( ).
A. c>0 B.2a+b=0 D. a-b+c>0
3.二次函数 与反比例函数 在同一平面直角坐标系中的图象大致为( ).
4.已知抛物线 的顶点为D(--1,2),与x轴的一个交点A 在(-3,0)和(--2,0)之间,其部分图象如图所示,则下列结论:①b -4ac<0;②a+b+c<0;③c-a=2;④方程 有两个相等的实数根.其中,正确的结论有( ).
A.1个 B.2个 C.3个 D.4个
5.已知抛物线 与x轴的交点都在原点的右侧,则点 M(a,c)在第 象限.
6.已知二次函数 的图象开口向下,顶点落在第二象限.
(1)试确定a,(b, 的符号,并简述理由.
(2)若此二次函数的图象经过原点,且顶点在直线x+y=0上,顶点与原点的距离为 ,求抛物线的二次函数的表达式.
7.已知函数 的顶点为点D.
(1)求点 D 的坐标(用含 m 的代数式表示).
(2)求函数 的图象与x轴的交点坐标.
(3)若函数 的图象在直线y=m的上方,求m的取值范围.
能力提升
8.已知抛物线 a是常数且a<0,下列选项中,可能为它的大致图象的是( ).
9.二次函数 的图象如图所示,现有下列结论:①4ac-b <0;②4a+c<2b;③3b+2c<0;④m(am+b)+b
C.2个 D.1个
10.二次函数 的图象的顶点在第一象限,且过点(-1,0).设t=a+b+1,则t的取值范围是 .
11.已知二次函数 的图象如图所示,则 的值为 ,c/a的取值范围是 .
12.如图所示为抛物线 的图象,A,B,C为抛物线与坐标轴的交点,且OA=OC=1,则a,b之间满足的关系式为 .
13.对于二次函数 如果当x取任意整数时,函数值y都是整数,那么我们把该函数的图象叫做“整点抛物线”(例如:
(1)请你写出一个二次项系数的绝对值小于1的“整点抛物线”的函数表达式: .(不必证明)
(2)请探索:是否存在二次项系数的绝对值小于 的“整点抛物线” 若存在,请写出其中一条抛物线的表达式;若不存在,请说明理由.
夯实演练
14.已知二次函数 图象的对称轴为直线x=1,其图象如图所示,现有下列结论:①abc>0;②b-2a<0;③a-b+c>0;④a+b>n(an+b)(n≠1);⑤2c<3b.其中,正确的是( ).
A.①③ B.②⑤
C.③④ D.④⑤
15.在平面直角坐标系中,设二次函数 其中a≠0.
(1)若函数 y1 的图象经过点(1,-2),求函数 y1的表达式.
(2)若一次函数 的图象与y2的图象经过x轴上的同一点,探究实数a,b满足的表达式.
(3)已知点 P(x1,m)和点 Q(1,n)在函数 y1的图象上,若 求x1的取值范围.
16.如图所示,二次函数 图象的顶点为 H,与x轴交于A,B两点(点 B在点A 右侧),点 H,B关于直线l: 对称.
(1)求A,B两点的坐标,并证明点 A 在直线l上.
(2)求二次函数的表达式.
(3)过点 B作直线. 交直线l于点K. M,N分别为直线AH 和直线l上的两个动点,连结 HN,NM,MK,求 的最小值.
专题复习二 二次函数图象与系数的关系
1. C 2. D 3. A 4. C 5.三
6.(1)∵抛物线开口向下,∴a<0.
∵顶点在第二象限,
(2)由题意可得c=0,此时顶点坐标为
∵顶点在直线x+y=0上, 此时顶点坐标为
或 (舍去).
∴抛物线的函数表达式为
∴顶点 D(m,-m ).
(2)令 y=0,得 解得
∴函数的图象与x轴的交点坐标为(0,0),(2m,0).
(3)∵函数 的图象在直线y=m的上方,
∴顶点 D 在直线y=m的上方.
即
∴m的取值范围是-1
即
由图象知当x=-2时,y>0,即4a-2b+c>0①,
当x=-1时,y<0,即a-b+c<0②,
将b=-2a代入①②,得c>-8a,c<-3a.
又
12. a-b+1=0
(2)假设存在符合条件的抛物线,则对于抛物线 bx+c,
当x=0时,y=c;当x=1时,y=a+b+c.
由整点抛物线定义知:c为整数,a+b+c为整数,∴a+b必为整数.
当x=2时,y=4a+2b+c=2a+2(a+b)+c是整数,∴2a必为整数.
∴不存在二次项系数的绝对值小于 的“整点抛物线”.
14. D 【解析】①由图象可知a<0,b>0,c>0, abc<0,故①错误.
②由于a<0,所以-2a>0.又b>0,所以b-2a>0,故②错误.
③当x=-1时,y=a-b+c<0,故③错误.
④当x=1时,y的值最大,此时y=a+b+c.
而当x=n时,
故 ,即a+b>n(an+b),故④正确.
⑤当x=3时函数值小于0,y=9a+3b+c<0,且该抛物线对称轴是直线 即 代入得 得2c<3b,故⑤正确.
故④⑤正确.故选 D.
15.(1)由函数y 的图象经过点(1,-2),
得(a+1)(-a)=-2,解得(
当 时,
当 时,
综上所述,函数y 的表达式为
(2)当y=0时,(x+a)(x-a-1)=0,解得. =a+1.
∴y 的图象与x轴的交点是(-a,0),(a+1,0).
当 经过(-a,0)时, 即 当y = ax+b经过(a+1,0)时, 即
(3)由题意知,函数 y 的对称轴为直线
当点 P 在对称轴的左侧(含顶点)时,y随x 的增大而减小,
(1,n)与(0,n)关于对称轴对称,
由 m
∴点 A 的坐标为(-3,0),点 B 的坐标为(1,0).
∵直线
当x=-3时
∴点A 在直线l上.
(2)∵点 H,B关于过点A 的直线 对称,∴AH=AB=4.
∵AH=BH,∴△ABH为正三角形.
如答图1所示,过顶点 H 作 HC⊥AB 于点C,则 AC=
∴顶点 H(-1,2 ),代入二次函数表达式,解得 a
∴二次函数表达式为
(3)易求得直线AH的函数表达式为 直线BK 的函数表达式为
日 解得
即 K(3,2 ).∴BK=4.
∵点 H,B关于直线AK 对称,
∴HN+MN的最小值是MB.
如答图2 所示,过点 K 作直线 AH 的对称点 Q,连结QK,交直线AH于点E,
则QM=MK,QE=EK=KD=2 ,则 AE⊥QK.
∴BM+MK 的最小值是BQ,即 BQ的长是HN+NM+MK 的最小值.
∵BK∥AH,∴∠BKQ=∠HEQ=90°.
由勾股定理可求得 QB=8.
∴HN+NM+MK 和的最小值为8.
同课章节目录
