第1章二次函数 单元测试卷 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 第1章二次函数 单元测试卷 提优训练(含答案)2024-2025学年浙教版九年级数学上册 | 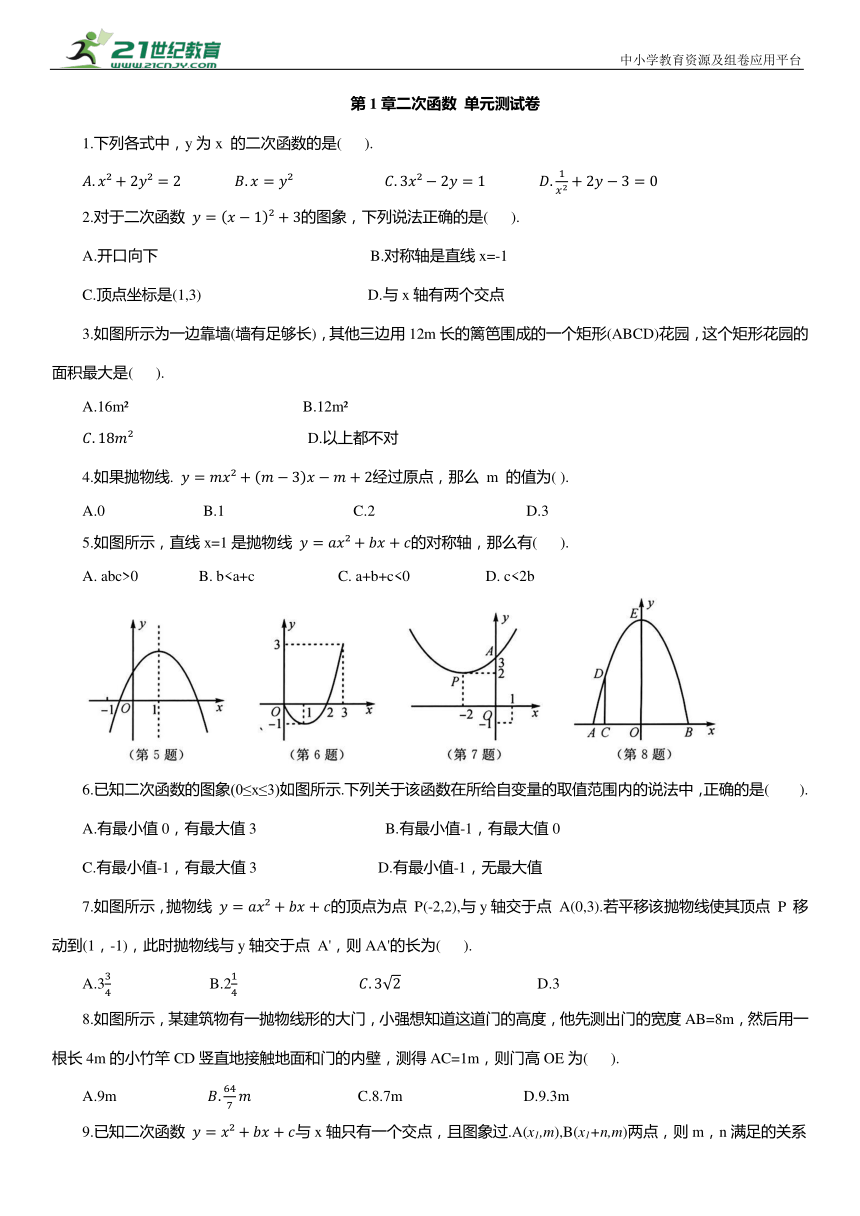 | |
| 格式 | docx | ||
| 文件大小 | 310.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 09:46:12 | ||
图片预览





文档简介
第1章二次函数 单元测试卷
1.下列各式中,y为x 的二次函数的是( ).
2.对于二次函数 的图象,下列说法正确的是( ).
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,3) D.与x轴有两个交点
3.如图所示为一边靠墙(墙有足够长),其他三边用12m长的篱笆围成的一个矩形(ABCD)花园,这个矩形花园的面积最大是( ).
A.16m B.12m
D.以上都不对
4.如果抛物线. 经过原点,那么 m 的值为( ).
A.0 B.1 C.2 D.3
5.如图所示,直线x=1是抛物线 的对称轴,那么有( ).
A. abc>0 B. b6.已知二次函数的图象(0≤x≤3)如图所示.下列关于该函数在所给自变量的取值范围内的说法中,正确的是( ).
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
7.如图所示,抛物线 的顶点为点 P(-2,2),与y轴交于点 A(0,3).若平移该抛物线使其顶点 P 移动到(1,-1),此时抛物线与y轴交于点 A',则AA'的长为( ).
A.3 B.2 D.3
8.如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长4m的小竹竿CD竖直地接触地面和门的内壁,测得AC=1m,则门高OE为( ).
A.9m C.8.7m D.9.3m
9.已知二次函数 与x轴只有一个交点,且图象过.A(x1,m),B(x1+n,m)两点,则m,n满足的关系为( ).
10.已知二次函数 ,当m≤x≤n且 mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( ).
A. B.2 C. D.
11.如果某个二次函数的图象经过平移后能与 的图象重合,那么这个二次函数的表达式为 (只需写出一个).
12.如图所示,抛物线 的对称轴是过点(1,0)且平行于 y轴的直线.若点 P(5,0)在抛物线上,则9a-3b+c的值为 .
13.如图所示,抛物线 与x 轴相交于点A,B(m+2,0),与y轴相交于点C,点D 在该抛物线上,坐标为(m,c),则点 A 的坐标是 .
14.某公司的新产品上市30天全部售完,图1表示该产品上市后的日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则该产品的最大日销售利润是 元.
15.二次函数 的图象如图所示,若线段AB在x轴上,且AB 为2 个单位,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为 .
16.如图所示,过点A(1,0),B(3,0)作x轴的垂线,分别交直线y=4-x于C,D两点,连结OC,OD,抛物线 经过O,C,D三点.若将△AOC沿CD 方向平移(点C在线段CD 上,且不与点 D 重合),在平移的过程中,△AOC与△OBD重叠部分的面积记为S,则S的最大值为 .
17.已知抛物线的顶点坐标是(2,-3),且经过点
(1)求这个抛物线的函数表达式,并作出这个函数的大致图象.
(2)当x在什么范围内时,y随x的增大而增大 当x在什么范围内时,y随x的增大而减小
18.今有网球从斜坡点O处抛出,网球的运动轨迹是抛物线 的图象的一段,斜坡的截线OA 是一次函数 的图象的一段,建立如图所示的平面直角坐标系.
(1)求网球抛出的最高点的坐标.
(2)求网球在斜坡上的落点 A 的竖直高度.
19.若直线 与二次函数 的图象交于A,B两点(点A 在点 B 的左侧).
(1)求 A,B两点的坐标.
(2)求 的面积.
(3)x为何值时,一次函数的值大于二次函数的值
20.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫的距离为x(km),乘坐地铁的时间. 是关于x的一次函数,其关系如下表所示:
地铁站 A B C D E
x(km) 8 9 10 11.5 13
y1(min) 18 20 22 25 28
(1)求 y1关于x的函数表达式.
(2)李华骑单车的时间也受x的影响,其关系可以用 来描述,问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短 并求出最短时间.
21.已知二次函数 的图象与x轴只有一个公共点A.
(1)当 时,求点 A 的坐标.
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥-1时,求点 B的横坐标m 的取值范围.
22.在平面直角坐标系中,已知抛物线 的顶点为A,点B 的坐标为(3,5).
(1)求抛物线过点 B 时顶点 A 的坐标.
(2)将点 A 的坐标记为(x,y),求y关于x的函数表达式.
(3)已知点C的坐标为(0,2),当m取何值时,抛物线 与线段 BC 只有一个交点.
23.如图所示,抛物线 的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求该抛物线的函数表达式.
(2)抛物线的顶点M与对称轴l上的点 N关于x轴对称,直线 AN 交抛物线于点 D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点 E 的坐标.
(3)在(2)的条件下,P为抛物线上一动点,Q为对称轴上一动点,抛物线上是否存在一点P,使以A,D,P,Q为顶点的四边形为平行四边形 若存在,求出点 P 的坐标;若不存在,请说明理由.
1. C 2. C 3. C 4. C 5. D 6. C 7. A 8. B 9. D
10. D 【解析】二次函数. 的大致图象如答图所示:
①当m≤0≤x≤n<1时,当x=m时y取最小值,即 2m=--(m- ,解得m=-2 或m=2(舍去).
当x=n时y 取最大值,即 2n=
解得n=2或n=-2(均不合题意,舍去).
②当m≤0≤x≤1≤n时,当x=m时y取最小值,由①知m=-2.
当x=1时y取最大值,
即 解得
或x=n时y取最小值,x=1时y取最大值,
∵m<0,∴此种情形不合题意.
故选 D.
11. y=3(x+2) +3 12.0 13.(-2,0) 14.1800
15.(2,-3)或(
16. 【解析】∵过点 A(1,0),B(3,0)作x轴的垂线,分别交直线 y=4-x于C,D两点,∴C(1,3),D(3,1).∴直线OC 的函数表达式为y=3x,直线OD 的函数表达式为 设平移后的三角形为△A'O'C',点 C'在线段CD 上,设O'C'与x轴交于点E,与直线OD交于点 P,设A'C'与x轴交于点F,与直线OD交于点Q,如答图所示.设水平方向的平移距离为 t(0≤t<2),则AF=t,F(1+t,0), 设直线O'C'的函数表达式为y=3x+b,将( 代入得b=-4t,∴直线O'C'的函数表达式为y=3x-4t.
由 解得
过点 P 作PG⊥x轴于点G,则 .∴当t=1时,S有最大值
17.(1)设抛物线的函数表达式为 把((1, 代入,得 即
∴抛物线的函数表达式为 图略.
(2)∵抛物线对称轴为直线x=2,且a>0,∴当x≥2时,y随x的增大而增大;当x≤2时,y随x的增大而减小.
∴网球抛出的最高点的坐标为(4,8).
(2)由题意得 解得x=0或x=7.
中小学教育资源及组卷应用平台
当x=7时,
∴网球在斜坡的落点 A 的垂直高度为-
19.(1)由题意得 解得 或
∴A,B两点的坐标分别为(0,3),(1,4).
(2)∵A,B 两点的坐标分别是(0,3),(1,4),
∴OA=3,OA边上的高线长是1.
(3)当x<0或x>1时,一次函数的值大于二次函数的值.
20.(1)设 y = kx+b,将(8,18),(9,20)代入,
得 解得
∴y 关于x的函数表达式为
(2)设李华从文化宫回到家所需的时间为 y.
则
∴当x=9时,y有最小值.
∴李华应选择在B站出地铁,才能使他从文化宫回到家所需的时间最短,最短为 39.5min.
21.(1)∵二次函数 的图象与x轴只有一个公共点A,.
∴二次函数的表达式为
当y=0时, 解得x =x =1,∴A(1,0).
当y=0时,
将点 代入y=x+k,得
F 消去y得 解得
∵点 A 的横坐标为 点 B 的横坐标
∵2>0,∴当 时,m随 的增大而减小.
即:m≥3.
22.(1)∵抛物线 过点 B(3,5),∴把 B(3,5)代入 整理得 解得
当m=1时, 顶点 A 的坐标为(1,1).
当m=3时, 顶点 A 的坐标为(3,5).
综上所述,顶点 A 的坐标为(1,1)或(3,5).
∴顶点 A 的坐标为(m,2m-1).
∵点 A 的坐标记为(x,y),∴x=m. ∴y=2x-1.
(3)由(2)可知,抛物线的顶点在直线y=2x-1上运动,且抛物线形状不变,由(1)知,当m=1或3时,抛物线过点 B(3,5).
把C(0,2)代入 得 1=2,解得m=1或-3.
∴当m=1或-3时,抛物线经过点 C(0,2).
如答图所示,当m=-3或3时,抛物线与线段 BC 只有一个交点(即线段CB的端点).
当m=1时,抛物线同时过点 B,C,不合题意.
∴m的取值范围是-3≤m≤3且m≠1.
23.(1)∵抛物线 的图象经过A(1,0),B(3,0),
∴设抛物线的函数表达式为y=a(x-1)(x-3).
∵抛物线y=a(x-1)(x-3)(a≠0)的图象经过点 C(0,6),
∴6=a(0-1)(0-3).∴a=2.
∴抛物线的函数表达式为 +6.
∴顶点 M 的坐标为(2,-2).
∵抛物线的顶点 M与对称轴l上的点 N 关于x轴对称,∴点 N(2,2).
设直线 AN的函数表达式为y= kx+b.
由题意得 解得
∴直线 AN的函数表达式为y=2x-2.
联立方程组 解得
设点 E(m,2m-2).
∵直线 BE将△ABD的面积分为1:2两部分,
或
或
∴m=2 或3.∴点 E的坐标为(2,2)或(3,4).
(3)若AD为平行四边形的边:
∵以A,D,P,Q为顶点的四边形为平行四边形,
或
或 xp=2-4+1=-1.
∴点 P 坐标为(5,16)或(-1,16).
若AD为平行四边形的对角线:
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD与PQ互相平分.
·点 P 坐标为(3,0).
综上所述,当点 P 坐标为(5,16)或(-1,16)或(3,0)时,以A,D,P,Q为顶点的四边形为平行四边形.
1.下列各式中,y为x 的二次函数的是( ).
2.对于二次函数 的图象,下列说法正确的是( ).
A.开口向下 B.对称轴是直线x=-1
C.顶点坐标是(1,3) D.与x轴有两个交点
3.如图所示为一边靠墙(墙有足够长),其他三边用12m长的篱笆围成的一个矩形(ABCD)花园,这个矩形花园的面积最大是( ).
A.16m B.12m
D.以上都不对
4.如果抛物线. 经过原点,那么 m 的值为( ).
A.0 B.1 C.2 D.3
5.如图所示,直线x=1是抛物线 的对称轴,那么有( ).
A. abc>0 B. b
A.有最小值0,有最大值3 B.有最小值-1,有最大值0
C.有最小值-1,有最大值3 D.有最小值-1,无最大值
7.如图所示,抛物线 的顶点为点 P(-2,2),与y轴交于点 A(0,3).若平移该抛物线使其顶点 P 移动到(1,-1),此时抛物线与y轴交于点 A',则AA'的长为( ).
A.3 B.2 D.3
8.如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长4m的小竹竿CD竖直地接触地面和门的内壁,测得AC=1m,则门高OE为( ).
A.9m C.8.7m D.9.3m
9.已知二次函数 与x轴只有一个交点,且图象过.A(x1,m),B(x1+n,m)两点,则m,n满足的关系为( ).
10.已知二次函数 ,当m≤x≤n且 mn<0时,y的最小值为2m,最大值为2n,则m+n的值为( ).
A. B.2 C. D.
11.如果某个二次函数的图象经过平移后能与 的图象重合,那么这个二次函数的表达式为 (只需写出一个).
12.如图所示,抛物线 的对称轴是过点(1,0)且平行于 y轴的直线.若点 P(5,0)在抛物线上,则9a-3b+c的值为 .
13.如图所示,抛物线 与x 轴相交于点A,B(m+2,0),与y轴相交于点C,点D 在该抛物线上,坐标为(m,c),则点 A 的坐标是 .
14.某公司的新产品上市30天全部售完,图1表示该产品上市后的日销售量与上市时间之间的关系,图2表示单件产品的销售利润与上市时间之间的关系,则该产品的最大日销售利润是 元.
15.二次函数 的图象如图所示,若线段AB在x轴上,且AB 为2 个单位,以AB为边作等边△ABC,使点C落在该函数y轴右侧的图象上,则点C的坐标为 .
16.如图所示,过点A(1,0),B(3,0)作x轴的垂线,分别交直线y=4-x于C,D两点,连结OC,OD,抛物线 经过O,C,D三点.若将△AOC沿CD 方向平移(点C在线段CD 上,且不与点 D 重合),在平移的过程中,△AOC与△OBD重叠部分的面积记为S,则S的最大值为 .
17.已知抛物线的顶点坐标是(2,-3),且经过点
(1)求这个抛物线的函数表达式,并作出这个函数的大致图象.
(2)当x在什么范围内时,y随x的增大而增大 当x在什么范围内时,y随x的增大而减小
18.今有网球从斜坡点O处抛出,网球的运动轨迹是抛物线 的图象的一段,斜坡的截线OA 是一次函数 的图象的一段,建立如图所示的平面直角坐标系.
(1)求网球抛出的最高点的坐标.
(2)求网球在斜坡上的落点 A 的竖直高度.
19.若直线 与二次函数 的图象交于A,B两点(点A 在点 B 的左侧).
(1)求 A,B两点的坐标.
(2)求 的面积.
(3)x为何值时,一次函数的值大于二次函数的值
20.随着地铁和共享单车的发展,“地铁+单车”已成为很多市民出行的选择,李华从文化宫站出发,先乘坐地铁,准备在离家较近的A,B,C,D,E中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与文化宫的距离为x(km),乘坐地铁的时间. 是关于x的一次函数,其关系如下表所示:
地铁站 A B C D E
x(km) 8 9 10 11.5 13
y1(min) 18 20 22 25 28
(1)求 y1关于x的函数表达式.
(2)李华骑单车的时间也受x的影响,其关系可以用 来描述,问:李华应选择在哪一站出地铁,才能使他从文化宫回到家所需的时间最短 并求出最短时间.
21.已知二次函数 的图象与x轴只有一个公共点A.
(1)当 时,求点 A 的坐标.
(2)过点A的直线y=x+k与二次函数的图象相交于另一点B,当b≥-1时,求点 B的横坐标m 的取值范围.
22.在平面直角坐标系中,已知抛物线 的顶点为A,点B 的坐标为(3,5).
(1)求抛物线过点 B 时顶点 A 的坐标.
(2)将点 A 的坐标记为(x,y),求y关于x的函数表达式.
(3)已知点C的坐标为(0,2),当m取何值时,抛物线 与线段 BC 只有一个交点.
23.如图所示,抛物线 的图象经过A(1,0),B(3,0),C(0,6)三点.
(1)求该抛物线的函数表达式.
(2)抛物线的顶点M与对称轴l上的点 N关于x轴对称,直线 AN 交抛物线于点 D,直线BE交AD于点E,若直线BE将△ABD的面积分为1:2两部分,求点 E 的坐标.
(3)在(2)的条件下,P为抛物线上一动点,Q为对称轴上一动点,抛物线上是否存在一点P,使以A,D,P,Q为顶点的四边形为平行四边形 若存在,求出点 P 的坐标;若不存在,请说明理由.
1. C 2. C 3. C 4. C 5. D 6. C 7. A 8. B 9. D
10. D 【解析】二次函数. 的大致图象如答图所示:
①当m≤0≤x≤n<1时,当x=m时y取最小值,即 2m=--(m- ,解得m=-2 或m=2(舍去).
当x=n时y 取最大值,即 2n=
解得n=2或n=-2(均不合题意,舍去).
②当m≤0≤x≤1≤n时,当x=m时y取最小值,由①知m=-2.
当x=1时y取最大值,
即 解得
或x=n时y取最小值,x=1时y取最大值,
∵m<0,∴此种情形不合题意.
故选 D.
11. y=3(x+2) +3 12.0 13.(-2,0) 14.1800
15.(2,-3)或(
16. 【解析】∵过点 A(1,0),B(3,0)作x轴的垂线,分别交直线 y=4-x于C,D两点,∴C(1,3),D(3,1).∴直线OC 的函数表达式为y=3x,直线OD 的函数表达式为 设平移后的三角形为△A'O'C',点 C'在线段CD 上,设O'C'与x轴交于点E,与直线OD交于点 P,设A'C'与x轴交于点F,与直线OD交于点Q,如答图所示.设水平方向的平移距离为 t(0≤t<2),则AF=t,F(1+t,0), 设直线O'C'的函数表达式为y=3x+b,将( 代入得b=-4t,∴直线O'C'的函数表达式为y=3x-4t.
由 解得
过点 P 作PG⊥x轴于点G,则 .∴当t=1时,S有最大值
17.(1)设抛物线的函数表达式为 把((1, 代入,得 即
∴抛物线的函数表达式为 图略.
(2)∵抛物线对称轴为直线x=2,且a>0,∴当x≥2时,y随x的增大而增大;当x≤2时,y随x的增大而减小.
∴网球抛出的最高点的坐标为(4,8).
(2)由题意得 解得x=0或x=7.
中小学教育资源及组卷应用平台
当x=7时,
∴网球在斜坡的落点 A 的垂直高度为-
19.(1)由题意得 解得 或
∴A,B两点的坐标分别为(0,3),(1,4).
(2)∵A,B 两点的坐标分别是(0,3),(1,4),
∴OA=3,OA边上的高线长是1.
(3)当x<0或x>1时,一次函数的值大于二次函数的值.
20.(1)设 y = kx+b,将(8,18),(9,20)代入,
得 解得
∴y 关于x的函数表达式为
(2)设李华从文化宫回到家所需的时间为 y.
则
∴当x=9时,y有最小值.
∴李华应选择在B站出地铁,才能使他从文化宫回到家所需的时间最短,最短为 39.5min.
21.(1)∵二次函数 的图象与x轴只有一个公共点A,.
∴二次函数的表达式为
当y=0时, 解得x =x =1,∴A(1,0).
当y=0时,
将点 代入y=x+k,得
F 消去y得 解得
∵点 A 的横坐标为 点 B 的横坐标
∵2>0,∴当 时,m随 的增大而减小.
即:m≥3.
22.(1)∵抛物线 过点 B(3,5),∴把 B(3,5)代入 整理得 解得
当m=1时, 顶点 A 的坐标为(1,1).
当m=3时, 顶点 A 的坐标为(3,5).
综上所述,顶点 A 的坐标为(1,1)或(3,5).
∴顶点 A 的坐标为(m,2m-1).
∵点 A 的坐标记为(x,y),∴x=m. ∴y=2x-1.
(3)由(2)可知,抛物线的顶点在直线y=2x-1上运动,且抛物线形状不变,由(1)知,当m=1或3时,抛物线过点 B(3,5).
把C(0,2)代入 得 1=2,解得m=1或-3.
∴当m=1或-3时,抛物线经过点 C(0,2).
如答图所示,当m=-3或3时,抛物线与线段 BC 只有一个交点(即线段CB的端点).
当m=1时,抛物线同时过点 B,C,不合题意.
∴m的取值范围是-3≤m≤3且m≠1.
23.(1)∵抛物线 的图象经过A(1,0),B(3,0),
∴设抛物线的函数表达式为y=a(x-1)(x-3).
∵抛物线y=a(x-1)(x-3)(a≠0)的图象经过点 C(0,6),
∴6=a(0-1)(0-3).∴a=2.
∴抛物线的函数表达式为 +6.
∴顶点 M 的坐标为(2,-2).
∵抛物线的顶点 M与对称轴l上的点 N 关于x轴对称,∴点 N(2,2).
设直线 AN的函数表达式为y= kx+b.
由题意得 解得
∴直线 AN的函数表达式为y=2x-2.
联立方程组 解得
设点 E(m,2m-2).
∵直线 BE将△ABD的面积分为1:2两部分,
或
或
∴m=2 或3.∴点 E的坐标为(2,2)或(3,4).
(3)若AD为平行四边形的边:
∵以A,D,P,Q为顶点的四边形为平行四边形,
或
或 xp=2-4+1=-1.
∴点 P 坐标为(5,16)或(-1,16).
若AD为平行四边形的对角线:
∵以A,D,P,Q为顶点的四边形为平行四边形,
∴AD与PQ互相平分.
·点 P 坐标为(3,0).
综上所述,当点 P 坐标为(5,16)或(-1,16)或(3,0)时,以A,D,P,Q为顶点的四边形为平行四边形.
同课章节目录
