3.1 圆(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.1 圆(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 319.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 21:17:28 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.1 圆(2)
基础巩固
1.确定一个圆的条件是( ).
A.已知圆心 B.已知半径
C.已知直径 D.过一个三角形的三个顶点
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( ).
A.第①块 B.第②块 C.第③块 D.第④块
3.如图所示,点A,B,C分别表示三个村庄,AB=1000m,BC=600m,AC=800m,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心 P 的位置应在( ).
A. AB中点 B. BC中点
C. AC中点 D.∠C的平分线与AB 的交点
4.如图所示,在平面直角坐标中,△ABC为直角三角形,∠ABC=90°,AB垂直于x轴,点M为Rt△ABC的外心.若点A 的坐标为(3,4),点 M 的坐标为(-1,1),则点 B 的坐标为( ).
A.(3,-1) B.(3,-2) C.(3,-3) D.(3,-4)
5.如图所示,平面直角坐标系中一条圆弧经过网格点 A,B,C,其中点 B 的坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
6.如图所示,正方形网格中的每个小正方形的边长都相等.△ABC的三个顶点A,B,C都在格点上,若格点 D(点 D 与点A,B,C均不重合)在△ABC外接圆上,则图中符合条件的点 D 有 个.
7.阅读材料:对于平面图形A,若存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A 被这个圆所覆盖.根据以上材料,回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是 cm.
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是 cm.
8.作图题:
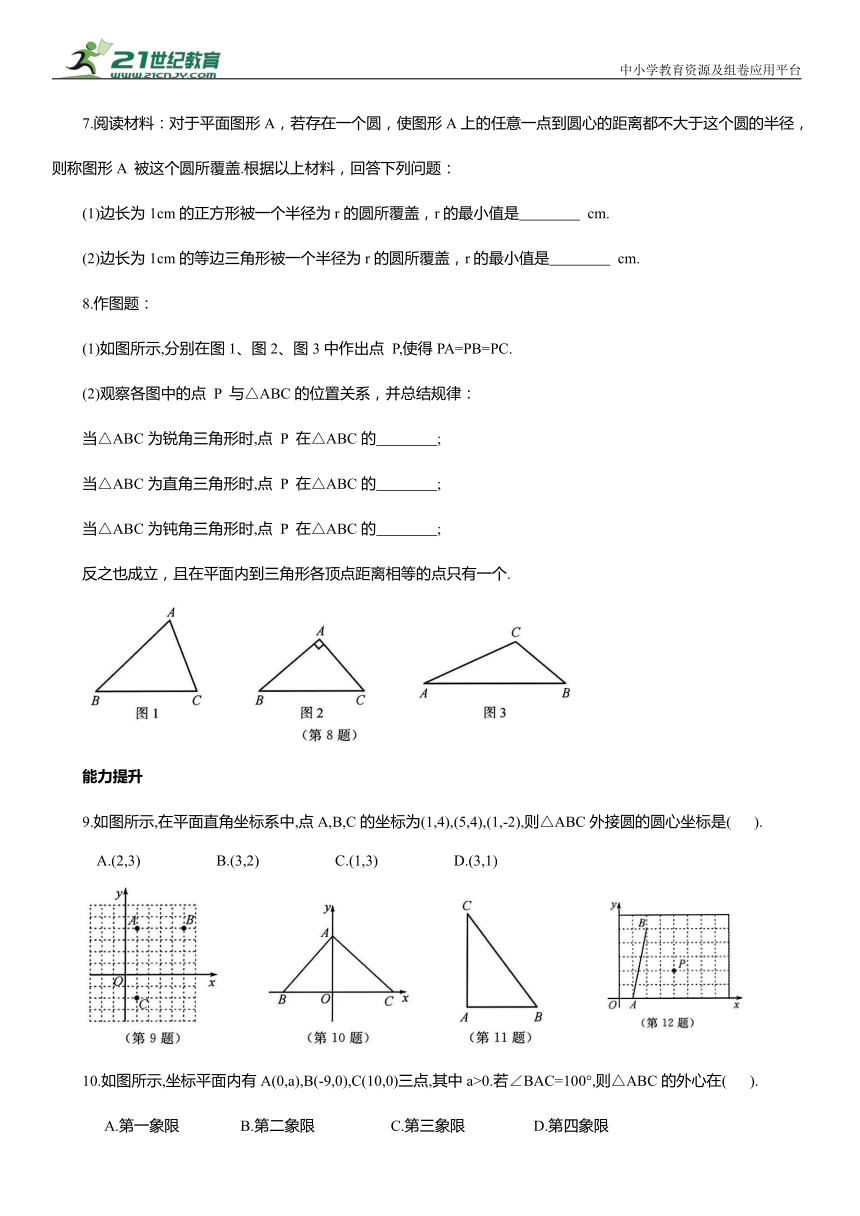
(1)如图所示,分别在图1、图2、图3中作出点 P,使得PA=PB=PC.
(2)观察各图中的点 P 与△ABC的位置关系,并总结规律:
当△ABC为锐角三角形时,点 P 在△ABC的 ;
当△ABC为直角三角形时,点 P 在△ABC的 ;
当△ABC为钝角三角形时,点 P 在△ABC的 ;
反之也成立,且在平面内到三角形各顶点距离相等的点只有一个.
能力提升
9.如图所示,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( ).
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
10.如图所示,坐标平面内有A(0,a),B(-9,0),C(10,0)三点,其中a>0.若∠BAC=100°,则△ABC的外心在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.根据三角形外心的概念,我们可以引入一个新定义:到三角形的两个顶点距离相等的点,叫做三角形的“准外心”.根据“准外心”的定义,探究如下问题:如图所示,在 Rt△ABC中,∠A=90°,BC=10,AB=6,若“准外心”点 P在AC边上,则 PA 的长为 .
12.如图所示,在平面直角坐标系中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,点 P 是△ABC的外心,则点 C的坐标为 .
13.如图1所示,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE.
(2)如图2所示,当点 D 是△ABC外接圆的圆心时,请判断四边形 BDCE的形状,并证明你的结论.
夯实演练
14.如图所示,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
15.已知半径为5 的⊙O是锐角三角形ABC 的外接圆,AB=AC,连结OB,OC,延长CO交弦AB 于点 D.若△OBD是直角三角形,则弦 BC的长为 .
16.如图所示,已知点 H 是△ABC的垂心,点O是外心,OL⊥BC 于点L.求证:AH=2OL.
3.1 圆(2)
1. D 2. B 3. A 4. B 5.(2,0) 6.5
7.(1)π/2(2)
8.(1)略 (2)内部 斜边的中点上外部
9. D 10. D 11.4或 12.(7,4)或(6,5)或(1,4)
13.(1)∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD.
∴∠ABD=∠CBE.
在△ABD与△CBE中,∴
∴△ABD≌△CBE.
(2)四边形 BDCE是菱形.
证明:同(1)可证△ABD≌△CBE,∴CE=AD.
∵点 D 是△ABC外接圆圆心,∴DA=DB=DC.
∵BD=BE,∴BD=BE=CE=CD.
∴四边形 BDCE是菱形.
14.5
15.5 或5 【解析】如答图1 所示,当∠ODB=90°时,CD⊥AB,∴AD=BD.∴AC=BC.
∵AB=AC,∴△ABC是等边三角形.∴∠DBO=30°.
如答图2所示,当∠DOB=90°时,∠BOC=90°,∴△BOC是等腰直角三角形.
综上所述,若△OBD是直角三角形,则弦 BC的长为5 或5
16.如答图所示,作 OM⊥AC 于点M,取 CH 的中点 K,连结 MK,LK,则有 MK∥AH∥OL,LK ∥BH∥OM,
∴四边形OLKM为平行四边形.
∴MK=OL.
3.1 圆(2)
基础巩固
1.确定一个圆的条件是( ).
A.已知圆心 B.已知半径
C.已知直径 D.过一个三角形的三个顶点
2.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是( ).
A.第①块 B.第②块 C.第③块 D.第④块
3.如图所示,点A,B,C分别表示三个村庄,AB=1000m,BC=600m,AC=800m,在社会主义新农村建设中,为了丰富群众生活,拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心 P 的位置应在( ).
A. AB中点 B. BC中点
C. AC中点 D.∠C的平分线与AB 的交点
4.如图所示,在平面直角坐标中,△ABC为直角三角形,∠ABC=90°,AB垂直于x轴,点M为Rt△ABC的外心.若点A 的坐标为(3,4),点 M 的坐标为(-1,1),则点 B 的坐标为( ).
A.(3,-1) B.(3,-2) C.(3,-3) D.(3,-4)
5.如图所示,平面直角坐标系中一条圆弧经过网格点 A,B,C,其中点 B 的坐标为(4,4),则该圆弧所在圆的圆心坐标为 .
6.如图所示,正方形网格中的每个小正方形的边长都相等.△ABC的三个顶点A,B,C都在格点上,若格点 D(点 D 与点A,B,C均不重合)在△ABC外接圆上,则图中符合条件的点 D 有 个.
7.阅读材料:对于平面图形A,若存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称图形A 被这个圆所覆盖.根据以上材料,回答下列问题:
(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是 cm.
(2)边长为1cm的等边三角形被一个半径为r的圆所覆盖,r的最小值是 cm.
8.作图题:
(1)如图所示,分别在图1、图2、图3中作出点 P,使得PA=PB=PC.
(2)观察各图中的点 P 与△ABC的位置关系,并总结规律:
当△ABC为锐角三角形时,点 P 在△ABC的 ;
当△ABC为直角三角形时,点 P 在△ABC的 ;
当△ABC为钝角三角形时,点 P 在△ABC的 ;
反之也成立,且在平面内到三角形各顶点距离相等的点只有一个.
能力提升
9.如图所示,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( ).
A.(2,3) B.(3,2) C.(1,3) D.(3,1)
10.如图所示,坐标平面内有A(0,a),B(-9,0),C(10,0)三点,其中a>0.若∠BAC=100°,则△ABC的外心在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
11.根据三角形外心的概念,我们可以引入一个新定义:到三角形的两个顶点距离相等的点,叫做三角形的“准外心”.根据“准外心”的定义,探究如下问题:如图所示,在 Rt△ABC中,∠A=90°,BC=10,AB=6,若“准外心”点 P在AC边上,则 PA 的长为 .
12.如图所示,在平面直角坐标系中,点A,B,P的坐标分别为(1,0),(2,5),(4,2).若点C在第一象限内,且横坐标、纵坐标均为整数,点 P 是△ABC的外心,则点 C的坐标为 .
13.如图1所示,在△ABC中,BA=BC,D是平面内不与点A,B,C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE.
(2)如图2所示,当点 D 是△ABC外接圆的圆心时,请判断四边形 BDCE的形状,并证明你的结论.
夯实演练
14.如图所示,点A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为 .
15.已知半径为5 的⊙O是锐角三角形ABC 的外接圆,AB=AC,连结OB,OC,延长CO交弦AB 于点 D.若△OBD是直角三角形,则弦 BC的长为 .
16.如图所示,已知点 H 是△ABC的垂心,点O是外心,OL⊥BC 于点L.求证:AH=2OL.
3.1 圆(2)
1. D 2. B 3. A 4. B 5.(2,0) 6.5
7.(1)π/2(2)
8.(1)略 (2)内部 斜边的中点上外部
9. D 10. D 11.4或 12.(7,4)或(6,5)或(1,4)
13.(1)∵∠ABC=∠DBE,
∴∠ABC+∠CBD=∠DBE+∠CBD.
∴∠ABD=∠CBE.
在△ABD与△CBE中,∴
∴△ABD≌△CBE.
(2)四边形 BDCE是菱形.
证明:同(1)可证△ABD≌△CBE,∴CE=AD.
∵点 D 是△ABC外接圆圆心,∴DA=DB=DC.
∵BD=BE,∴BD=BE=CE=CD.
∴四边形 BDCE是菱形.
14.5
15.5 或5 【解析】如答图1 所示,当∠ODB=90°时,CD⊥AB,∴AD=BD.∴AC=BC.
∵AB=AC,∴△ABC是等边三角形.∴∠DBO=30°.
如答图2所示,当∠DOB=90°时,∠BOC=90°,∴△BOC是等腰直角三角形.
综上所述,若△OBD是直角三角形,则弦 BC的长为5 或5
16.如答图所示,作 OM⊥AC 于点M,取 CH 的中点 K,连结 MK,LK,则有 MK∥AH∥OL,LK ∥BH∥OM,
∴四边形OLKM为平行四边形.
∴MK=OL.
同课章节目录
