3.5 圆周角(1) 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.5 圆周角(1) 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 337.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 21:14:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.5 圆周角(1)
基础巩固
1.如图所示,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数为( ).
A.15° B.20° C.25° D.30°
2.如图所示,AB 是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( ).
A.100° B.110° C.115° D.120°
3.如图所示,在⊙O中,AB是直径,BC是弦,点 P 是上任意一点.若AB=5,BC=3,则AP 的长不可能为( ).
A.3 B.4 C. D.5
4.如图所示,AB是⊙O的直径,CD 是⊙O的弦,∠ACD=30°,则∠BAD 的度数为( ).
A.30° B.50° C.60° D.70°
5.如图所示,在△ABC中,AB=AC.以AB 为直径作半⊙O,交 BC 于点D.若∠BAC=40°,则 的度数是 .
6.如图所示,△ABD是⊙O的内接三角形,圆心O在边AB 上,C为的中点,AD分别与BC,OC交于E,F两点.求证:
(1)OF∥BD.
(2)若∠C=30°,则AD平分OC.
能力提升
7.如图所示,A,B,C,D是⊙O上的四个点,B是 的中点,M是半径OD 上任意一点.若∠BDC=40°,则∠AMB 的度数不可能是( ).
A.45° B.60° C.75° D.85°
8.如图所示,⊙O的直径AB 为8,P 是上半圆(点A,B除外)上任一点,∠APB的平分线交⊙O于点C,弦EF过AC,BC的中点M,N,则EF 的长是( ).
C.6
9. AB为半圆O的直径,现将一把等腰直角三角尺按如图所示的方式放置,锐角顶点 P 在半圆上,斜边过点 B,一条直角边交该半圆于点 Q. 若AB=2,则线段 BQ 的长为 .
10.我们把1°的圆心角所对的弧叫做1°的弧.圆心角∠AOB的度数等于它所对的弧 的度数,记为: 由此可知:命题“圆周角的度数等于其所对的弧的度数的一半”是真命题,请结合图1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题.
(1)如图2所示,⊙O的两条弦AB,CD相交于圆内一点 P,求证:
(2)如图3所示,若⊙O的两条弦AB,CD相交于圆外一点 P,则(1)中的结论是否成立 如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明).
夯实演练
11.如图所示,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,∠ACD=45°,则∠ADB 的度数为( ).
A.55° B.60°
C.65° D.70°
12.如图所示,∠BAC 的平分线交△ABC 的外接圆于点 D,∠ABC的平分线交AD 于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
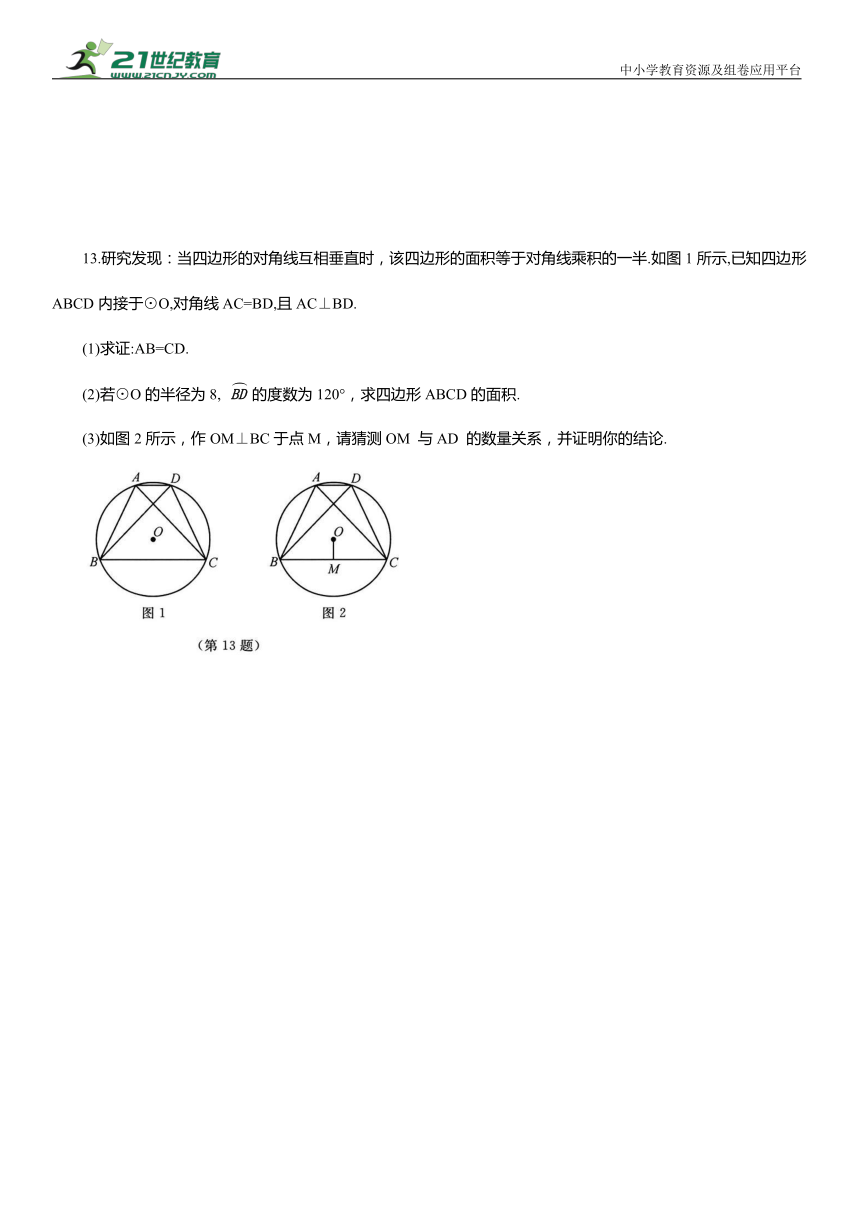
13.研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图1所示,已知四边形ABCD内接于⊙O,对角线AC=BD,且AC⊥BD.
(1)求证:AB=CD.
(2)若⊙O的半径为8, 的度数为120°,求四边形ABCD的面积.
(3)如图2所示,作OM⊥BC于点M,请猜测OM 与AD 的数量关系,并证明你的结论.
3.5 圆周角(1)
1. D 2. B 3. A 4. C 5.140°
6.(1)∵OC为半径,点C为AD中点,∴AF=DF.
∵AO=BO,∴OF∥BD.
(2)如答图所示,延长 CO 交⊙O于点 N.
∵∠C=30°,∴∠BON=60°.
∵∠AOC=∠BON,
∵OC为半径,C为AD中点,
∴OF⊥AD.∴∠OFA=90°.∴∠A=30°.
即 AD平分OC.
7. D 8. A 9.
即圆周角的度数等于其所对的弧的度数的一半.
(1)如答图所示,连结 BC,则∠APC=∠PCB+∠PBC.
(2)(1)中的结论不成立.
类似的结论为:
11. C
12.(1)∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵∠DBC=∠CAD,∴∠DBC=∠BAD.
∵BE平分∠ABC,∴∠ABE=∠CBE.
又∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAD,
∴∠DBE=∠DEB.∴DE=DB.
(2)如答图所示,连结CD.
由(1)得
∴CD=BD=4.
∵∠BAC=90°,∴BC是直径.
∴∠BDC=90°.
∴△ABC外接圆的半径
13.(1)∵AC=BD,∴AC=BD.则AB=DC,∴AB=CD.
(2)如答图所示,连结OB,OD,作OH⊥BD于点 H,
的度数为120°,
∴∠BOD=120°.∴∠BOH=60°.
则
则四边形ABCD的面积
(3)AD=2OM.
证明:如答图2所示,连结OB,OC,OA,OD,作 OE⊥AD于点E.
∵OE⊥AD,∴AE=DE.
∵∠BOC=2∠BAC,而∠BOC=2∠BOM,
∴∠BOM=∠BAC.
同理可得∠AOE=∠ABD.
∵BD⊥AC,∴∠BAC+∠ABD=90°.
∴∠BOM+∠AOE=90°.
∵∠BOM+∠OBM=90°,∴∠OBM=∠AOE.
在△BOM和△OAE中,·
∴△BOM≌△OAE.
∴OM=AE.∴AD=2OM.
3.5 圆周角(1)
基础巩固
1.如图所示,在⊙O中,OD⊥BC,∠BOD=60°,则∠CAD的度数为( ).
A.15° B.20° C.25° D.30°
2.如图所示,AB 是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( ).
A.100° B.110° C.115° D.120°
3.如图所示,在⊙O中,AB是直径,BC是弦,点 P 是上任意一点.若AB=5,BC=3,则AP 的长不可能为( ).
A.3 B.4 C. D.5
4.如图所示,AB是⊙O的直径,CD 是⊙O的弦,∠ACD=30°,则∠BAD 的度数为( ).
A.30° B.50° C.60° D.70°
5.如图所示,在△ABC中,AB=AC.以AB 为直径作半⊙O,交 BC 于点D.若∠BAC=40°,则 的度数是 .
6.如图所示,△ABD是⊙O的内接三角形,圆心O在边AB 上,C为的中点,AD分别与BC,OC交于E,F两点.求证:
(1)OF∥BD.
(2)若∠C=30°,则AD平分OC.
能力提升
7.如图所示,A,B,C,D是⊙O上的四个点,B是 的中点,M是半径OD 上任意一点.若∠BDC=40°,则∠AMB 的度数不可能是( ).
A.45° B.60° C.75° D.85°
8.如图所示,⊙O的直径AB 为8,P 是上半圆(点A,B除外)上任一点,∠APB的平分线交⊙O于点C,弦EF过AC,BC的中点M,N,则EF 的长是( ).
C.6
9. AB为半圆O的直径,现将一把等腰直角三角尺按如图所示的方式放置,锐角顶点 P 在半圆上,斜边过点 B,一条直角边交该半圆于点 Q. 若AB=2,则线段 BQ 的长为 .
10.我们把1°的圆心角所对的弧叫做1°的弧.圆心角∠AOB的度数等于它所对的弧 的度数,记为: 由此可知:命题“圆周角的度数等于其所对的弧的度数的一半”是真命题,请结合图1给予证明(不要求写已知、求证,只需直接证明),并解决以下的问题.
(1)如图2所示,⊙O的两条弦AB,CD相交于圆内一点 P,求证:
(2)如图3所示,若⊙O的两条弦AB,CD相交于圆外一点 P,则(1)中的结论是否成立 如果成立,给予证明;如果不成立,写出一个类似的结论(不要求证明).
夯实演练
11.如图所示,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,∠ACD=45°,则∠ADB 的度数为( ).
A.55° B.60°
C.65° D.70°
12.如图所示,∠BAC 的平分线交△ABC 的外接圆于点 D,∠ABC的平分线交AD 于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径.
13.研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半.如图1所示,已知四边形ABCD内接于⊙O,对角线AC=BD,且AC⊥BD.
(1)求证:AB=CD.
(2)若⊙O的半径为8, 的度数为120°,求四边形ABCD的面积.
(3)如图2所示,作OM⊥BC于点M,请猜测OM 与AD 的数量关系,并证明你的结论.
3.5 圆周角(1)
1. D 2. B 3. A 4. C 5.140°
6.(1)∵OC为半径,点C为AD中点,∴AF=DF.
∵AO=BO,∴OF∥BD.
(2)如答图所示,延长 CO 交⊙O于点 N.
∵∠C=30°,∴∠BON=60°.
∵∠AOC=∠BON,
∵OC为半径,C为AD中点,
∴OF⊥AD.∴∠OFA=90°.∴∠A=30°.
即 AD平分OC.
7. D 8. A 9.
即圆周角的度数等于其所对的弧的度数的一半.
(1)如答图所示,连结 BC,则∠APC=∠PCB+∠PBC.
(2)(1)中的结论不成立.
类似的结论为:
11. C
12.(1)∵AD平分∠BAC,∴∠BAD=∠CAD.
又∵∠DBC=∠CAD,∴∠DBC=∠BAD.
∵BE平分∠ABC,∴∠ABE=∠CBE.
又∵∠DBE=∠CBE+∠DBC,∠DEB=∠ABE+∠BAD,
∴∠DBE=∠DEB.∴DE=DB.
(2)如答图所示,连结CD.
由(1)得
∴CD=BD=4.
∵∠BAC=90°,∴BC是直径.
∴∠BDC=90°.
∴△ABC外接圆的半径
13.(1)∵AC=BD,∴AC=BD.则AB=DC,∴AB=CD.
(2)如答图所示,连结OB,OD,作OH⊥BD于点 H,
的度数为120°,
∴∠BOD=120°.∴∠BOH=60°.
则
则四边形ABCD的面积
(3)AD=2OM.
证明:如答图2所示,连结OB,OC,OA,OD,作 OE⊥AD于点E.
∵OE⊥AD,∴AE=DE.
∵∠BOC=2∠BAC,而∠BOC=2∠BOM,
∴∠BOM=∠BAC.
同理可得∠AOE=∠ABD.
∵BD⊥AC,∴∠BAC+∠ABD=90°.
∴∠BOM+∠AOE=90°.
∵∠BOM+∠OBM=90°,∴∠OBM=∠AOE.
在△BOM和△OAE中,·
∴△BOM≌△OAE.
∴OM=AE.∴AD=2OM.
同课章节目录
