3.6 圆内接四边形 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.6 圆内接四边形 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 383.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.6 圆内接四边形
基础巩固
1.在圆内接四边形 ABCD中,已知∠A=70°,则∠C的度数为( ).
A.20° B.30° C.70° D.110°
2.如图所示,四边形 ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的度数为( ).
A.80° B.100° C.60° D.40°
3.如图所示,四边形 ABCD是⊙O的内接四边形,AD与BC 的延长线交于点E,BA与CD 的延长线交于点F,∠DCE=80°,∠F=25°,则∠E 的度数为( ).
A.55° B.50° C.45° D.40°
4.如图所示,圆心角∠AOB=120°,P 是 上任意一点(不与点A,B重合),点C在线段AP 的延长线上,则∠BPC 的度数为( ).
A.45° B.60° C.75° D.85°
5.如图所示,BC为半圆O的直径,A,D为半圆上两点,若A为半圆弧 的中点,则∠ADC 的度数为 .
6.如图所示,⊙O是四边形ABCD 的外接圆,CE∥AD交AB于点E,BE=BC,∠BCD=122°,则∠ADC的度数为 .
7.如图所示,已知四边形 ABCD内一点E,若EA=EB=EC=ED,∠BAD=70°,则∠BCD的度数为 .
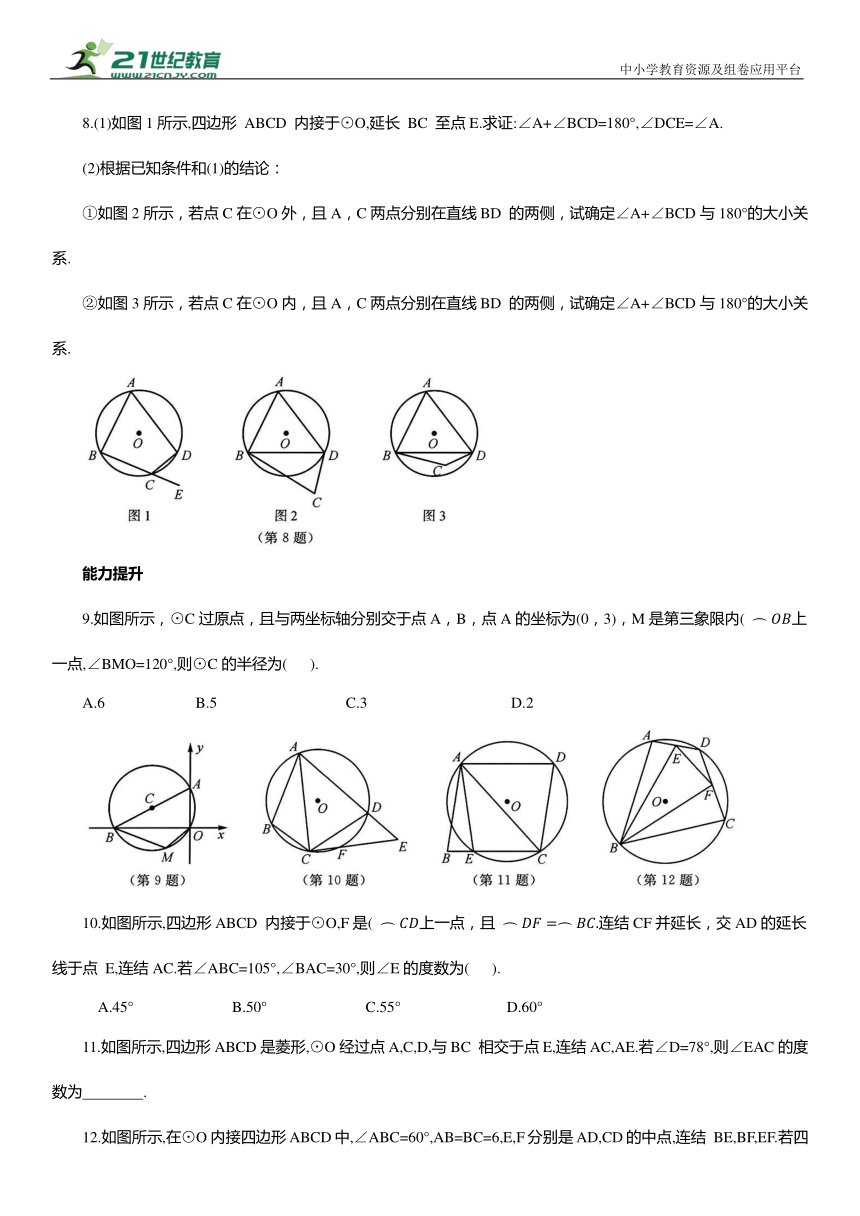
8.(1)如图1所示,四边形 ABCD 内接于⊙O,延长 BC 至点E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)根据已知条件和(1)的结论:
①如图2所示,若点C在⊙O外,且A,C两点分别在直线BD 的两侧,试确定∠A+∠BCD与180°的大小关系.
②如图3所示,若点C在⊙O内,且A,C两点分别在直线BD 的两侧,试确定∠A+∠BCD与180°的大小关系.
能力提升
9.如图所示,⊙C过原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是第三象限内( 上一点,∠BMO=120°,则⊙C的半径为( ).
A.6 B.5 C.3 D.2
10.如图所示,四边形ABCD 内接于⊙O,F是( 上一点,且 连结CF并延长,交AD的延长线于点 E,连结AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( ).
A.45° B.50° C.55° D.60°
11.如图所示,四边形ABCD是菱形,⊙O经过点A,C,D,与BC 相交于点E,连结AC,AE.若∠D=78°,则∠EAC的度数为 .
12.如图所示,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E,F分别是AD,CD的中点,连结 BE,BF,EF.若四边形 ABCD 的面积为 则△BEF 的面积为 .
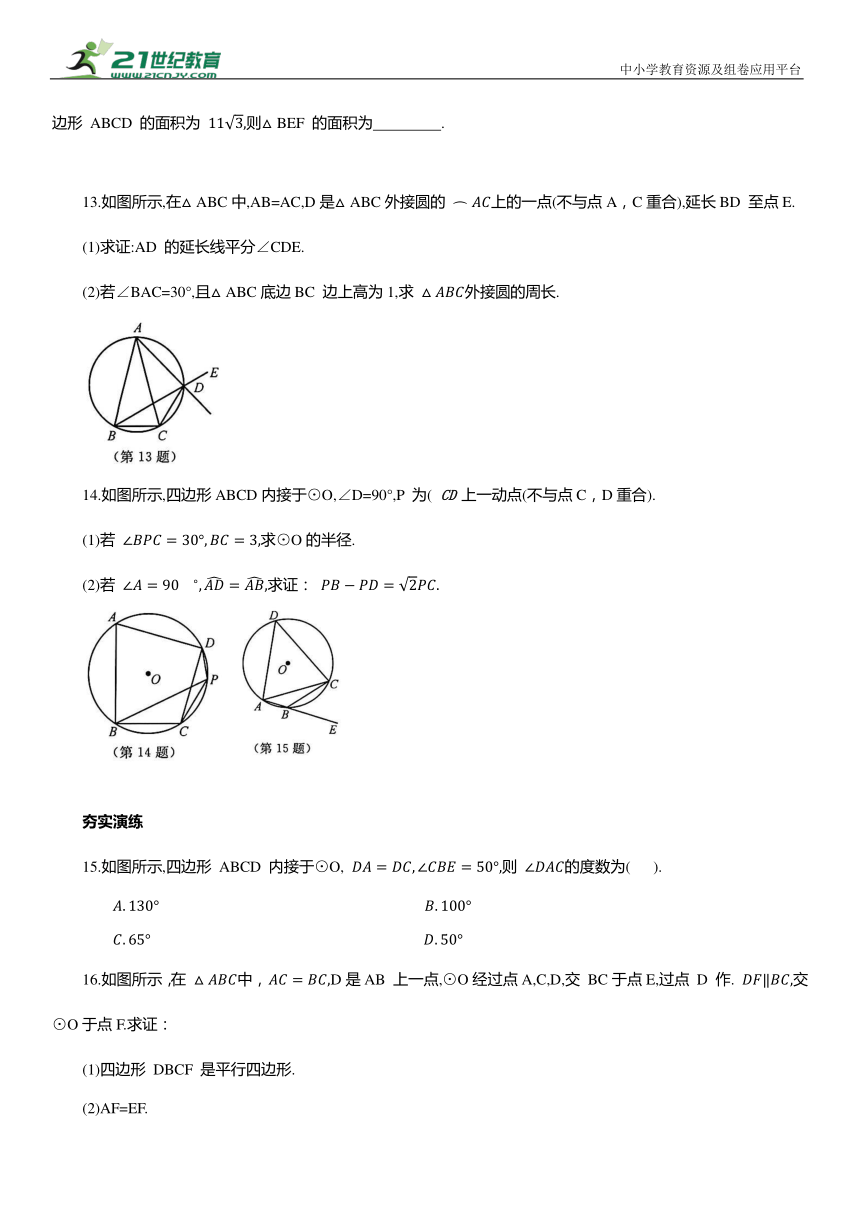
13.如图所示,在△ABC中,AB=AC,D是△ABC外接圆的 上的一点(不与点A,C重合),延长BD 至点E.
(1)求证:AD 的延长线平分∠CDE.
(2)若∠BAC=30°,且△ABC底边BC 边上高为1,求 外接圆的周长.
14.如图所示,四边形ABCD内接于⊙O,∠D=90°,P 为( 上一动点(不与点C,D重合).
(1)若 求⊙O的半径.
(2)若 求证:
夯实演练
15.如图所示,四边形 ABCD 内接于⊙O, 则 的度数为( ).
16.如图所示,在 中, D是AB 上一点,⊙O经过点A,C,D,交 BC于点E,过点 D 作. 交⊙O于点F.求证:
(1)四边形 DBCF 是平行四边形.
(2)AF=EF.
17.如图所示,四边形ABCD是⊙O的内接四边形,F是CD 延长线上的一点,且AD平分 于点E.
(1)求证:
(2)若 求CD的长.
1. D 2. A 3. C 4. B 5.135° 6.116° 7.110°
∵∠DCE+∠BCD=180°,∴∠DCE=∠A.
(2)①如答图1所示,连结 DE.
∵∠A+∠BED=180°,∠BED>∠BCD,
∴∠A+∠BCD<180°.
②如答图2所示,延长 DC交⊙O于点E,连结 BE.
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°.
9. C 10. A 11.27°
12.5 【解析】如答图所示,连结 AC,作 BM 垂直EF于点M,交 AC于点 N.
∵AE=ED,DF=FC,∴EF∥AC,EF= AC.
∵BM⊥EF,∴BM⊥AC.
∵BA=BC,∠ABC=60°,∴△ABC是等边三角形.
∵四边形 ABCD 的面积为
又‘
13.(1)如答图所示,设 F 为AD 延长线上一点.
∵A,B,C,D四点共圆,∴∠CDF=∠ABC.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ADB=∠ACB,∴∠ADB=∠CDF.
∵∠ADB=∠EDF,
∴∠EDF=∠CDF,即AD的延长线平分∠CDE.
(2)如答图所示,设O为外接圆圆心,连结 AO并延长,交 BC 于点H,连结OC.
∴AH⊥BC.
∴∠COH=2∠OAC=30°.
设圆半径为r,则
∵△ABC中BC 边上的高为1,
解得
∴△ABC的外接圆的周长为
14.(1)如答图所示,连结AC.
∵∠D=90°,
∴AC是⊙O的直径.
∵∠BAC=∠P=30°,
∴AC=2BC=6.
∴⊙O的半径为3.
(2)∵∠A=90°,∴∠BCD=90°.
∵AC为⊙O直径,∴∠D=∠ABC=90°.
∴四边形 ABCD为矩形.
∵AD=AB,∴AB=AD.∴矩形ABCD为正方形.
在 BP上截取BE=DP,
由 SAS易证△BCE≌△DCP.
∴PC=CE,∠BCE=∠DCP.
∵∠ECP=∠ECD+∠DCP=∠ECD+∠BCE=90°,
∴△CPE为等腰直角三角形.
即
15. C
16.(1)∵AC=BC,∴∠BAC=∠B.
∵DF∥BC,∴∠ADF=∠B.
∵∠BAC=∠CFD,∴∠ADF=∠CFD.∴BD∥CF.
∵DF∥BC,∴四边形 DBCF是平行四边形.
(2)连结 AE.
∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B.
∵四边形 AECF是⊙O的内接四边形,
∵BD∥CF,∴∠ECF+∠B=180°.∴∠EAF=∠B.
∴∠AEF=∠EAF.∴AF=EF.
17.(1)∵AD平分∠BDF,∴∠ADF=∠ADB.
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC.
∵∠ACB=∠ADB,∴∠ABC=∠ACB.∴AB=AC.
(2)如答图所示,过点A作AG⊥BD,垂足为点 G.
∵AD 平 分 ∠BDF, AE ⊥CF, AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°.
在 Rt△AED 和 Rt△AGD 中,
∴Rt△AED≌Rt△AGD.∴GD=ED=2.
在 Rt△AEC和 Rt△AGB中
∴Rt△AEC≌Rt△AGB.∴CE=BG.
∵BD=11,∴BG=BD-GD=11-2=9.
∴CE=BG=9.∴CD=CE-DE=9-2=7.
3.6 圆内接四边形
基础巩固
1.在圆内接四边形 ABCD中,已知∠A=70°,则∠C的度数为( ).
A.20° B.30° C.70° D.110°
2.如图所示,四边形 ABCD内接于⊙O,已知∠ADC=140°,则∠AOC的度数为( ).
A.80° B.100° C.60° D.40°
3.如图所示,四边形 ABCD是⊙O的内接四边形,AD与BC 的延长线交于点E,BA与CD 的延长线交于点F,∠DCE=80°,∠F=25°,则∠E 的度数为( ).
A.55° B.50° C.45° D.40°
4.如图所示,圆心角∠AOB=120°,P 是 上任意一点(不与点A,B重合),点C在线段AP 的延长线上,则∠BPC 的度数为( ).
A.45° B.60° C.75° D.85°
5.如图所示,BC为半圆O的直径,A,D为半圆上两点,若A为半圆弧 的中点,则∠ADC 的度数为 .
6.如图所示,⊙O是四边形ABCD 的外接圆,CE∥AD交AB于点E,BE=BC,∠BCD=122°,则∠ADC的度数为 .
7.如图所示,已知四边形 ABCD内一点E,若EA=EB=EC=ED,∠BAD=70°,则∠BCD的度数为 .
8.(1)如图1所示,四边形 ABCD 内接于⊙O,延长 BC 至点E.求证:∠A+∠BCD=180°,∠DCE=∠A.
(2)根据已知条件和(1)的结论:
①如图2所示,若点C在⊙O外,且A,C两点分别在直线BD 的两侧,试确定∠A+∠BCD与180°的大小关系.
②如图3所示,若点C在⊙O内,且A,C两点分别在直线BD 的两侧,试确定∠A+∠BCD与180°的大小关系.
能力提升
9.如图所示,⊙C过原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,3),M是第三象限内( 上一点,∠BMO=120°,则⊙C的半径为( ).
A.6 B.5 C.3 D.2
10.如图所示,四边形ABCD 内接于⊙O,F是( 上一点,且 连结CF并延长,交AD的延长线于点 E,连结AC.若∠ABC=105°,∠BAC=30°,则∠E的度数为( ).
A.45° B.50° C.55° D.60°
11.如图所示,四边形ABCD是菱形,⊙O经过点A,C,D,与BC 相交于点E,连结AC,AE.若∠D=78°,则∠EAC的度数为 .
12.如图所示,在⊙O内接四边形ABCD中,∠ABC=60°,AB=BC=6,E,F分别是AD,CD的中点,连结 BE,BF,EF.若四边形 ABCD 的面积为 则△BEF 的面积为 .
13.如图所示,在△ABC中,AB=AC,D是△ABC外接圆的 上的一点(不与点A,C重合),延长BD 至点E.
(1)求证:AD 的延长线平分∠CDE.
(2)若∠BAC=30°,且△ABC底边BC 边上高为1,求 外接圆的周长.
14.如图所示,四边形ABCD内接于⊙O,∠D=90°,P 为( 上一动点(不与点C,D重合).
(1)若 求⊙O的半径.
(2)若 求证:
夯实演练
15.如图所示,四边形 ABCD 内接于⊙O, 则 的度数为( ).
16.如图所示,在 中, D是AB 上一点,⊙O经过点A,C,D,交 BC于点E,过点 D 作. 交⊙O于点F.求证:
(1)四边形 DBCF 是平行四边形.
(2)AF=EF.
17.如图所示,四边形ABCD是⊙O的内接四边形,F是CD 延长线上的一点,且AD平分 于点E.
(1)求证:
(2)若 求CD的长.
1. D 2. A 3. C 4. B 5.135° 6.116° 7.110°
∵∠DCE+∠BCD=180°,∴∠DCE=∠A.
(2)①如答图1所示,连结 DE.
∵∠A+∠BED=180°,∠BED>∠BCD,
∴∠A+∠BCD<180°.
②如答图2所示,延长 DC交⊙O于点E,连结 BE.
∵∠A+∠E=180°,∠BCD>∠E,
∴∠A+∠BCD>180°.
9. C 10. A 11.27°
12.5 【解析】如答图所示,连结 AC,作 BM 垂直EF于点M,交 AC于点 N.
∵AE=ED,DF=FC,∴EF∥AC,EF= AC.
∵BM⊥EF,∴BM⊥AC.
∵BA=BC,∠ABC=60°,∴△ABC是等边三角形.
∵四边形 ABCD 的面积为
又‘
13.(1)如答图所示,设 F 为AD 延长线上一点.
∵A,B,C,D四点共圆,∴∠CDF=∠ABC.
∵AB=AC,∴∠ABC=∠ACB.
∵∠ADB=∠ACB,∴∠ADB=∠CDF.
∵∠ADB=∠EDF,
∴∠EDF=∠CDF,即AD的延长线平分∠CDE.
(2)如答图所示,设O为外接圆圆心,连结 AO并延长,交 BC 于点H,连结OC.
∴AH⊥BC.
∴∠COH=2∠OAC=30°.
设圆半径为r,则
∵△ABC中BC 边上的高为1,
解得
∴△ABC的外接圆的周长为
14.(1)如答图所示,连结AC.
∵∠D=90°,
∴AC是⊙O的直径.
∵∠BAC=∠P=30°,
∴AC=2BC=6.
∴⊙O的半径为3.
(2)∵∠A=90°,∴∠BCD=90°.
∵AC为⊙O直径,∴∠D=∠ABC=90°.
∴四边形 ABCD为矩形.
∵AD=AB,∴AB=AD.∴矩形ABCD为正方形.
在 BP上截取BE=DP,
由 SAS易证△BCE≌△DCP.
∴PC=CE,∠BCE=∠DCP.
∵∠ECP=∠ECD+∠DCP=∠ECD+∠BCE=90°,
∴△CPE为等腰直角三角形.
即
15. C
16.(1)∵AC=BC,∴∠BAC=∠B.
∵DF∥BC,∴∠ADF=∠B.
∵∠BAC=∠CFD,∴∠ADF=∠CFD.∴BD∥CF.
∵DF∥BC,∴四边形 DBCF是平行四边形.
(2)连结 AE.
∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B.
∵四边形 AECF是⊙O的内接四边形,
∵BD∥CF,∴∠ECF+∠B=180°.∴∠EAF=∠B.
∴∠AEF=∠EAF.∴AF=EF.
17.(1)∵AD平分∠BDF,∴∠ADF=∠ADB.
∵∠ABC+∠ADC=180°,∠ADC+∠ADF=180°,
∴∠ADF=∠ABC.
∵∠ACB=∠ADB,∴∠ABC=∠ACB.∴AB=AC.
(2)如答图所示,过点A作AG⊥BD,垂足为点 G.
∵AD 平 分 ∠BDF, AE ⊥CF, AG⊥BD,
∴AG=AE,∠AGB=∠AEC=90°.
在 Rt△AED 和 Rt△AGD 中,
∴Rt△AED≌Rt△AGD.∴GD=ED=2.
在 Rt△AEC和 Rt△AGB中
∴Rt△AEC≌Rt△AGB.∴CE=BG.
∵BD=11,∴BG=BD-GD=11-2=9.
∴CE=BG=9.∴CD=CE-DE=9-2=7.
同课章节目录
