3.5 圆周角(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.5 圆周角(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 377.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.5 圆周角(2)
基础巩固
1.如图所示,已知在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的度数为( ).
A.43° B.35° C.34° D.44°
2.如图所示,正方形 ABCD 内接于⊙O,E是 上任一点,则∠DEC的度数是( ).
A.30° B.45° C.60° D.80°
3.如图所示,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( ).
A.1 C.2 D.
4.已知在半径为2的⊙O中,圆内接△ABC的边 ,则∠C的度数为( ).
A.60° B.30° C.60°或120° D.30°或150°
5.如图所示,OB是⊙O的半径,AB=OB,直径CD⊥AB.若点 P 是线段OD 上的动点,连结 PA,则∠PAB 的度数可以是 (写出一个即可).
6.如图所示,⊙P 经过点A(0, ),O(0,0),B(1,0),点 C 在第一象限的 上,则∠BCO的度数为 .
7.如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点 D,AC交⊙O于点 E,∠BAC=45°.
(1)求∠EBC的度数.
(2)求证:BD=CD.
能力提升
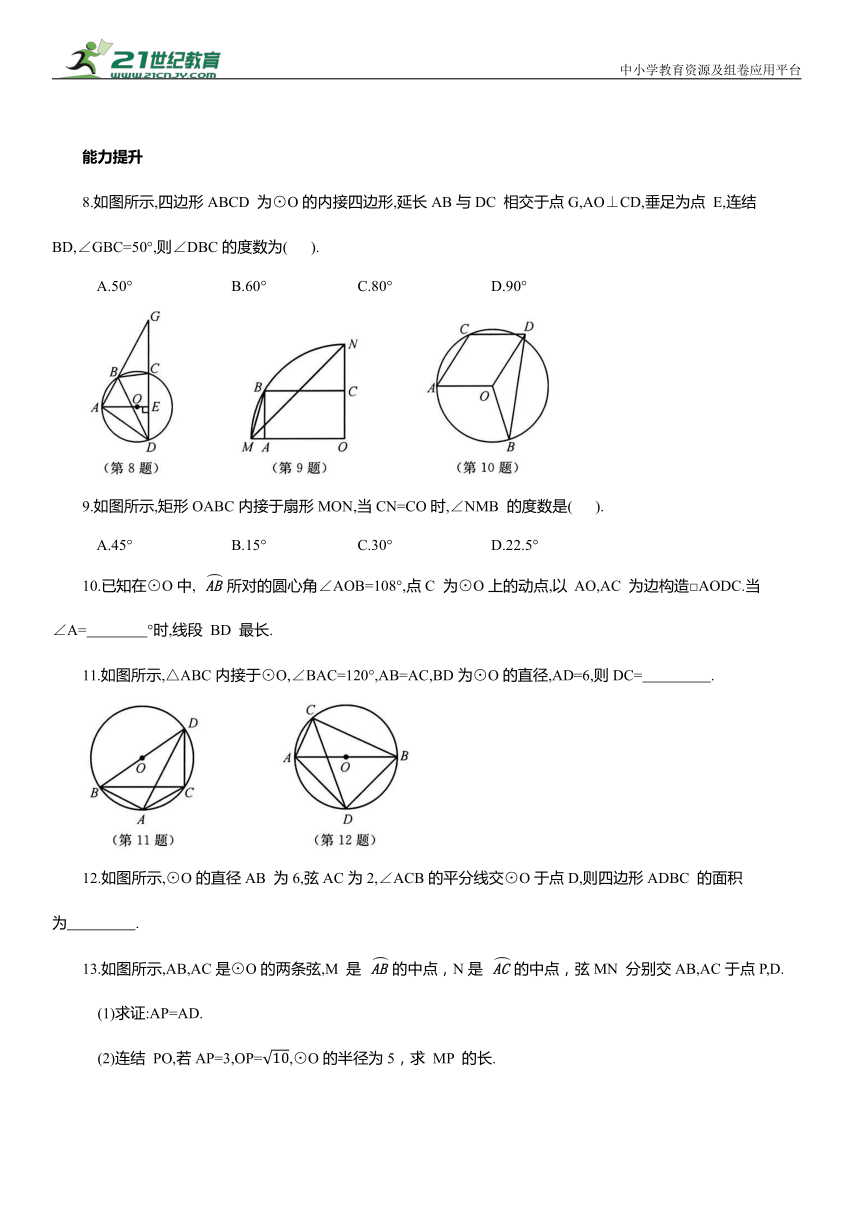
8.如图所示,四边形ABCD 为⊙O的内接四边形,延长AB与DC 相交于点G,AO⊥CD,垂足为点 E,连结 BD,∠GBC=50°,则∠DBC的度数为( ).
A.50° B.60° C.80° D.90°
9.如图所示,矩形OABC内接于扇形MON,当CN=CO时,∠NMB 的度数是( ).
A.45° B.15° C.30° D.22.5°
10.已知在⊙O中, 所对的圆心角∠AOB=108°,点C 为⊙O上的动点,以 AO,AC 为边构造□AODC.当∠A= °时,线段 BD 最长.
11.如图所示,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
12.如图所示,⊙O的直径AB 为6,弦AC为2,∠ACB的平分线交⊙O于点D,则四边形ADBC 的面积为 .
13.如图所示,AB,AC是⊙O的两条弦,M 是 的中点,N是 的中点,弦MN 分别交AB,AC于点P,D.
(1)求证:AP=AD.
(2)连结 PO,若AP=3,OP=,⊙O的半径为5,求 MP 的长.
夯实演练
14.如图所示,BD是⊙O 的直径,点 A,C在⊙O上, AC交BD 于点G.若∠COD=126°,则∠AGB的度数为( ).
A.99° B.108°
C.110° D.117°
15.如图所示,在⊙O中,弦AB与CD 相交于点E,AB=CD,连结AD,BC.求证:
(2)AE=CE.
16.如图1所示,⊙O中AB 是直径,C是⊙O上一点,∠ABC=45°,在等腰直角三角形DCE 中∠DCE 是直角,点 D 在线段AC 上.
(1)证明:B,C,E三点共线.
(2)若M 是线段BE 的中点,N 是线段AD 的中点,证明:
(3)如图2所示,将△DCE绕点C 按逆时针方向旋转 后,记为 若M1 是线段 BE1的中点,N1 是线段 AD1的中点, 是否成立 若成立,请证明;若不成立,请说明理由.
3.5 圆周角(2)
1. B 2. B 3. D 4. C 5.70° 6.30°
7.(1)∵AB是⊙O的直径,∴∠AEB=90°.
∵∠BAC=45°,∴∠ABE=45°.
∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°.
(2)如答图所示,连结AD.
∵AB是⊙O的直径,∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,∴BD=CD.
8. C 9. C
10.27 【解析】如答图所示,连结OC,延长AO交⊙O于点 F,连结 DF.
∵四边形 ACDO 是平行四 边 形, ∴ ∠DOF =∠CAO,DO=AC.
∵OF=AO,∴△DOF≌△CAO.
∴DF=OC.
∴点 D 的运动轨迹是以点 F 为圆心、OC为半径的圆.
∴当点 D在BF 的延长线上时,BD 的值最大.
∵∠AOB=108°,∴∠FOB=72°.
∵OF=OB,∴∠OFB=54°.
11.2 12.9+4
13.(1)如答图所示,连结AM,AN.
∴∠BAM=∠ANM,∠AMN=∠CAN.
∵∠APD =∠AMN +∠BAM,∠ADP =∠CAN +∠ANM,∴∠APD=∠ADP.∴AP=AD.
(2)如答图所示,连结AO,OM交AB 于点E,设PE=x.
∵AM=BM,∴OM⊥AB.∴∠AEO=90°.
解得x=1.
∴AE=4,OE=3,ME=2.
14. B
15.(1)∵AB=CD,∴AB=CD,|即
(2)由(1)知
∴∠ADE=∠CBE,∠DAE=∠BCE.
∴△ADE≌△CBE.∴AE=CE.
16.(1)∵AB是直径,∴∠BCA=90°.
∵在等腰直角三角形 DCE中∠DCE是直角,
∴∠BCA=∠DCE=90°.
∴∠BCA+∠DCE=180°.
∴B,C,E三点共线.
(2)如答图1所示,连结 BD,AE,ON,延长 BD交AE 于点F.
∵∠ABC=45°,∴CB=CA.
∵CD=CE,∴Rt△BCD≌Rt△ACE.
∴BD=AE,∠EBD=∠CAE.∴∠CAE+∠ADF=∠CBD+∠BDC=90°,即 BF⊥AE.
∵M是线段BE的中点,N是线段AD 的中点,O为AB的中点,
∴ON=OM,ON⊥OM.
∴△ONM为等腰直角三角形.
(3)成立.理由如下:如答图2所示,连结 BD ,AE ,ON .
与(2)同理可证△ON M 为等腰直角三角形,
3.5 圆周角(2)
基础巩固
1.如图所示,已知在⊙O中,弦AB,CD相交于点P,∠A=42°,∠APD=77°,则∠B的度数为( ).
A.43° B.35° C.34° D.44°
2.如图所示,正方形 ABCD 内接于⊙O,E是 上任一点,则∠DEC的度数是( ).
A.30° B.45° C.60° D.80°
3.如图所示,△ABC内接于⊙O,∠C=45°,AB=2,则⊙O的半径为( ).
A.1 C.2 D.
4.已知在半径为2的⊙O中,圆内接△ABC的边 ,则∠C的度数为( ).
A.60° B.30° C.60°或120° D.30°或150°
5.如图所示,OB是⊙O的半径,AB=OB,直径CD⊥AB.若点 P 是线段OD 上的动点,连结 PA,则∠PAB 的度数可以是 (写出一个即可).
6.如图所示,⊙P 经过点A(0, ),O(0,0),B(1,0),点 C 在第一象限的 上,则∠BCO的度数为 .
7.如图所示,AB为⊙O的直径,AB=AC,BC交⊙O于点 D,AC交⊙O于点 E,∠BAC=45°.
(1)求∠EBC的度数.
(2)求证:BD=CD.
能力提升
8.如图所示,四边形ABCD 为⊙O的内接四边形,延长AB与DC 相交于点G,AO⊥CD,垂足为点 E,连结 BD,∠GBC=50°,则∠DBC的度数为( ).
A.50° B.60° C.80° D.90°
9.如图所示,矩形OABC内接于扇形MON,当CN=CO时,∠NMB 的度数是( ).
A.45° B.15° C.30° D.22.5°
10.已知在⊙O中, 所对的圆心角∠AOB=108°,点C 为⊙O上的动点,以 AO,AC 为边构造□AODC.当∠A= °时,线段 BD 最长.
11.如图所示,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
12.如图所示,⊙O的直径AB 为6,弦AC为2,∠ACB的平分线交⊙O于点D,则四边形ADBC 的面积为 .
13.如图所示,AB,AC是⊙O的两条弦,M 是 的中点,N是 的中点,弦MN 分别交AB,AC于点P,D.
(1)求证:AP=AD.
(2)连结 PO,若AP=3,OP=,⊙O的半径为5,求 MP 的长.
夯实演练
14.如图所示,BD是⊙O 的直径,点 A,C在⊙O上, AC交BD 于点G.若∠COD=126°,则∠AGB的度数为( ).
A.99° B.108°
C.110° D.117°
15.如图所示,在⊙O中,弦AB与CD 相交于点E,AB=CD,连结AD,BC.求证:
(2)AE=CE.
16.如图1所示,⊙O中AB 是直径,C是⊙O上一点,∠ABC=45°,在等腰直角三角形DCE 中∠DCE 是直角,点 D 在线段AC 上.
(1)证明:B,C,E三点共线.
(2)若M 是线段BE 的中点,N 是线段AD 的中点,证明:
(3)如图2所示,将△DCE绕点C 按逆时针方向旋转 后,记为 若M1 是线段 BE1的中点,N1 是线段 AD1的中点, 是否成立 若成立,请证明;若不成立,请说明理由.
3.5 圆周角(2)
1. B 2. B 3. D 4. C 5.70° 6.30°
7.(1)∵AB是⊙O的直径,∴∠AEB=90°.
∵∠BAC=45°,∴∠ABE=45°.
∵AB=AC,
∴∠ABC=∠C=67.5°.
∴∠EBC=22.5°.
(2)如答图所示,连结AD.
∵AB是⊙O的直径,∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,∴BD=CD.
8. C 9. C
10.27 【解析】如答图所示,连结OC,延长AO交⊙O于点 F,连结 DF.
∵四边形 ACDO 是平行四 边 形, ∴ ∠DOF =∠CAO,DO=AC.
∵OF=AO,∴△DOF≌△CAO.
∴DF=OC.
∴点 D 的运动轨迹是以点 F 为圆心、OC为半径的圆.
∴当点 D在BF 的延长线上时,BD 的值最大.
∵∠AOB=108°,∴∠FOB=72°.
∵OF=OB,∴∠OFB=54°.
11.2 12.9+4
13.(1)如答图所示,连结AM,AN.
∴∠BAM=∠ANM,∠AMN=∠CAN.
∵∠APD =∠AMN +∠BAM,∠ADP =∠CAN +∠ANM,∴∠APD=∠ADP.∴AP=AD.
(2)如答图所示,连结AO,OM交AB 于点E,设PE=x.
∵AM=BM,∴OM⊥AB.∴∠AEO=90°.
解得x=1.
∴AE=4,OE=3,ME=2.
14. B
15.(1)∵AB=CD,∴AB=CD,|即
(2)由(1)知
∴∠ADE=∠CBE,∠DAE=∠BCE.
∴△ADE≌△CBE.∴AE=CE.
16.(1)∵AB是直径,∴∠BCA=90°.
∵在等腰直角三角形 DCE中∠DCE是直角,
∴∠BCA=∠DCE=90°.
∴∠BCA+∠DCE=180°.
∴B,C,E三点共线.
(2)如答图1所示,连结 BD,AE,ON,延长 BD交AE 于点F.
∵∠ABC=45°,∴CB=CA.
∵CD=CE,∴Rt△BCD≌Rt△ACE.
∴BD=AE,∠EBD=∠CAE.∴∠CAE+∠ADF=∠CBD+∠BDC=90°,即 BF⊥AE.
∵M是线段BE的中点,N是线段AD 的中点,O为AB的中点,
∴ON=OM,ON⊥OM.
∴△ONM为等腰直角三角形.
(3)成立.理由如下:如答图2所示,连结 BD ,AE ,ON .
与(2)同理可证△ON M 为等腰直角三角形,
同课章节目录
