第3章 圆的基本性质单元测试卷 (含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 第3章 圆的基本性质单元测试卷 (含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 607.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 22:00:12 | ||
图片预览



文档简介
第3章 圆的基本性质单元测试卷
1.在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,D是AB 边的中点,以点C为圆心、2.4cm为半径作圆,则点 D与⊙C的位置关系是( ).
A.点 D 在⊙C上 B.点 D 在⊙C外 C.点 D 在⊙C内 D.不能确定
2.如图所示,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( ).
A.40° B.50° C.80° D.100°
3.如图所示,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC的度数为( ).
A.100° B.112.5° C.120° D.135°
4.运用图形变化的方法研究下列问题:如图所示,AB是⊙O 的直径,CD,EF 是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( ).
B.10π C.24+4π D.24+5π
5.如图所示,在⊙O中,半径OC⊥弦AB,垂足为D,且AB=8,OC=5,则CD的长为( ).
A.3 B.2.5 C.2 D.1
6.观察下列图片及相应推理,其中正确的是( ).
∵∠AOB=∠A'OB', ∵AD=BC, 的度数为40°, ∵MN 垂直平分AD,
∴AB=CD. ∴∠AOB=80°.
7.如图所示,正六边形硬纸片ABCDEF 在桌面上由图1的起始位置沿直线不滑行地翻滚一周后到图 2位置.若正六边形的边长为2cm,则正六边形的中心O运动的路程为( ).
A.πcm B.2πcm
C.3πcm D.4πcm
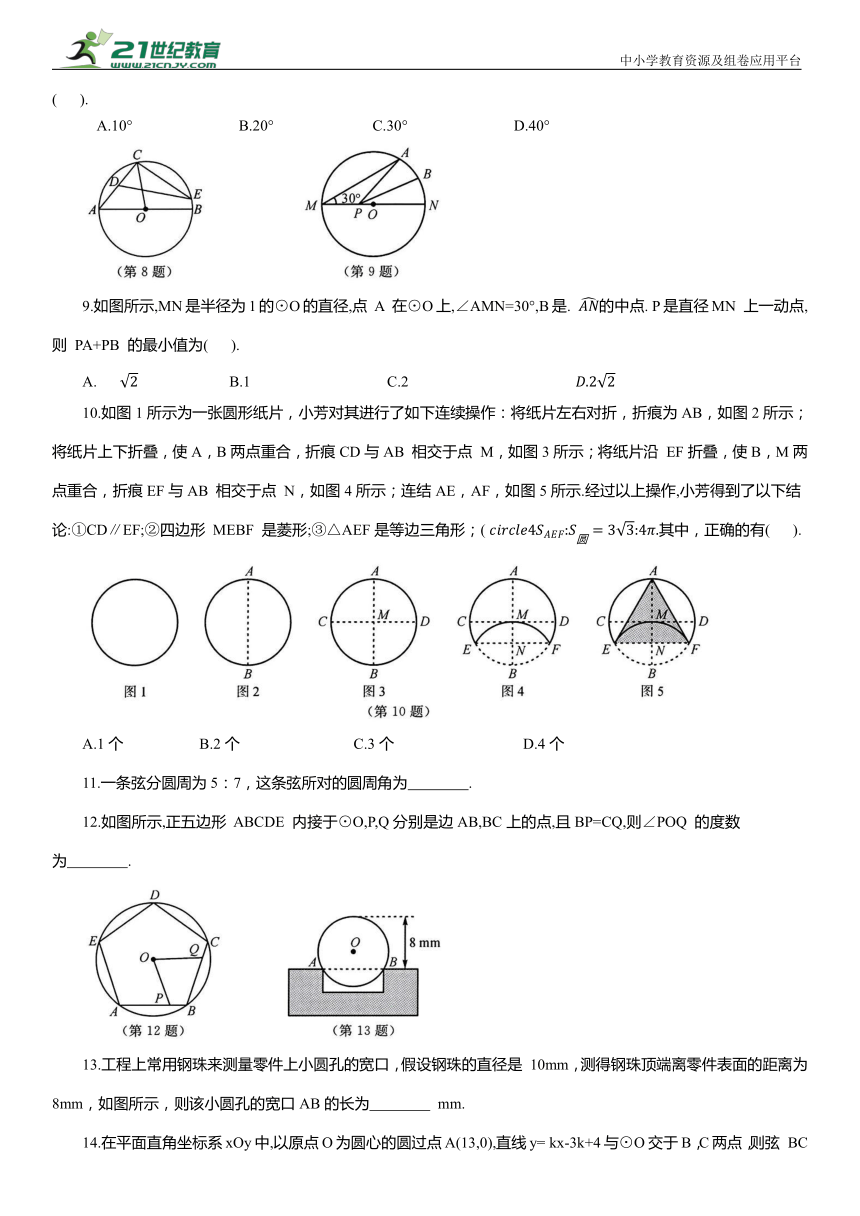
8.如图所示,在⊙O中,AB 为直径,∠AOC=80°,D为弦AC 的中点,E为 上任意一点,则∠CED 的度数可能是( ).
A.10° B.20° C.30° D.40°
9.如图所示,MN是半径为1的⊙O的直径,点 A 在⊙O上,∠AMN=30°,B是. 的中点. P是直径MN 上一动点,则 PA+PB 的最小值为( ).
A. B.1 C.2
10.如图1所示为一张圆形纸片,小芳对其进行了如下连续操作:将纸片左右对折,折痕为AB,如图2所示;将纸片上下折叠,使A,B两点重合,折痕CD与AB 相交于点 M,如图3所示;将纸片沿 EF折叠,使B,M两点重合,折痕EF与AB 相交于点 N,如图4所示;连结AE,AF,如图5所示.经过以上操作,小芳得到了以下结论:①CD∥EF;②四边形 MEBF 是菱形;③△AEF是等边三角形;( 其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
11.一条弦分圆周为5:7,这条弦所对的圆周角为 .
12.如图所示,正五边形 ABCDE 内接于⊙O,P,Q分别是边AB,BC上的点,且BP=CQ,则∠POQ 的度数为 .
13.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则该小圆孔的宽口AB的长为 mm.
14.在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y= kx-3k+4与⊙O交于B,C两点,则弦 BC 的长的最小值为 .
15.如图所示,在扇形 AOB中,∠AOB=90°,C是. 上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点 D,E.若DE=1,则扇形 AOB的面积为 .
16.正方形和圆都是人们比较喜欢的图形,给人以美感.某校数学兴趣小组在学习中发现:
(1)如图1所示,研究在以AB为直径的半圆中,裁剪出面积最大的正方形 CDEF时惊喜地发现,点C和点 F 其实分别是线段AF 和BC的黄金分割点.如果设圆的半径为r,那么此时正方形的边长(
(2)如图2所示,如果在半径为r的半圆中裁剪出两个同样大小且分别面积最大的正方形的边长( .如图3所示,并列n个正方形时的边长(
(3)如图4所示,当n=9时,我们还可以在第一层的上面再裁剪出同样大小的正方形,也可以再在第二层的上面再裁剪出第三层同样大小的正方形,则最多可以裁剪到第 层.
17.如图所示,在扇形AOB中,∠AOB=90°,正方形CDEF 的顶点C是 的中点,点 D在OB上,点E在OB的延长线上,当正方形CDEF 的边长为2 时,求阴影部分的面积.
18.如图所示,在平面直角坐标系中,直线l经过原点O,且与x轴正半轴的夹角为 点M在x轴上,⊙M半径为2,⊙M 与直线l相交于A,B两点,若 为等腰直角三角形,求点 M 的坐标.
19.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.若桥跨度AB约为40m,主拱高CD约10m.
(1)如图1所示,请通过尺规作图找到桥弧所在圆的圆心O(保留作图痕迹).
(2)如图2所示,求桥弧AB 所在圆的半径R.
20.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,延长CA交⊙O于点E,连结ED交AB 于点 F.
(1)求证:△CDE是等腰三角形.
(2)当 时,求 的值.
21.如图1所示,正方形ABCD内接于⊙O,E为上任意一点,连结DE,AE.
(1)求∠AED的度数.
(2)如图2所示,过点B作BF∥DE交⊙O于点 F,连结AF,AF=1,AE=4,求 DE的长.
22.已知⊙O中,AB=AC,P是 所对弧上一动点,连结 PB,PA.
(1)如图1所示,把 绕点A 按逆时针方向旋转到 求证:P,C,Q三点在同一条直线上.
(2)如图2所示,连结 PC,若 试探究 PA,PB,PC之间的关系,并说明理由.
(3)若∠BAC=120°,(2)中的结论是否成立 若成立,请证明;若不成立,请直接写出它们之间的数量关系,不需证明.
23.某班学习小组对无盖的纸杯进行制作与探究,所要制作的纸杯如图1所示,规格要求:杯口直径AB=6cm,杯底直径CD=4cm,杯壁母线AC=BD=6cm.请你和他们一起解决下列问题:
(1)小顾同学先画出了纸杯的侧面展开示意图(如图2中实线部分,忽略拼接部分),得到图形是圆环的一部分.
①图2中 的长为________,. 的长为___________,ME=NF=_______
②要想准确画出纸杯侧面的设计图,需要确定 所在圆的圆心O,如图2所示.小顾同学发现 之间存在以下关系 请你帮她证明这一结论.
③根据②中的结论,求 所在圆的半径r 及它所对的圆心角的度数n°.
(2)小顾同学计划利用矩形、正方形纸各一张,分别按如图3、图4所示的方式剪出这个纸杯的侧面,求矩形纸片的长和宽以及正方形纸片的边长.
1. B 2. D 3. B 4. A 5. C 6. B 7. D
8. C 【解析】如答图所示,连结OD,OE,BC.∵OC=OA,∴△OAC 是等腰三角形.∵D为弦AC 的中点,∴∠AOC=80°.
∴∠DOC=40°,∠BOC=100°.设∠BOE=x,则. +40°.
∵OC=OE,∠COE=100°-x,
∴∠OED<20°+ x.∴∠CED=∠OEC-∠OED>
中小学教育资源及组卷应用平台
∵∠CED<∠ABC=40°,∴20°<∠CED<40°.
故选 C.
9. A 10. D
11.75°或105° 12.72° 13.8 14.24 15.π/2
16.(1) , (2) , =,((3)5
17.如答图所示,连结OC.∵在扇形 AOB 中,∠AOB=90°,正方形 CDEF 的顶点C是AB的中点,
18.如答图所示,过点 M作MC⊥l于点C.
∵△MAB是等腰直角三角形,∴MA=MB.
∴∠BAM=∠ABM=45°.
∵MC⊥直线 l,
∴∠BAM=∠CMA=45°.∴AC=CM.
在Rt△ACM中,∵AC +CM =AM ,
即
在 Rt△OCM中,∠COM=30°,
根据对称性,在负半轴的点M(-2 ,0)也满足条件.
∴点 M 的坐标为(2 ,0)或(
19.(1)如答图所示.
(2)由(1)中的作图可知:△AOD为直角三角形,D是AB的中点.
∵CD=10m,∴OD=(R-10)m.
在 Rt△AOD中,由勾股定理得( 即 ,解得R=25.
∴桥弧 AB所在圆的半径R 为25m.
20.(1)∵AB=AC,∴∠ABC=∠C.
∵AD=AD,∴∠AED=∠ABC.
∴∠C=∠AED.∴△CDE是等腰三角形.
(2)如答图所示,连结AD,过点 D作DH⊥AE于点 H.
设
∵AB是直径,∴∠ADC=90°.
21.(1)如答图1 所示,连结OA,OD.
∵四边形ABCD是正方形,∴∠AOD=90°.
(2)如答图2所示,连结CF,CE,CA,BD,过点 D 作DH⊥AE 于点 H.
∵BF∥DE,∴∠FBD=∠EDB.
∵四边形ABCD是正方形,∴AB∥CD.
∴∠ABD=∠CDB.∴∠ABF=∠CDE.
∵∠CFA=∠AEC=90°,∴∠DEC=∠AFB=135°.
∵CD=AB,∴△CDE≌△ABF.∴CE=AF=1.
∵∠DHE=90°,∴∠HDE=∠HED=45°.
∴DH=HE.
设 DH=EH=x.
在 Rt△ADH 中,
解得 或
或
22.(1)如答图1所示,连结 PC.
∵把△ABP 绕点A 按逆时针方向旋转到△ACQ,
∴∠ABP=∠ACQ.
∵四边形ABPC为⊙O的内接四边形,
∴∠ABP+∠ACP=180°.∴∠ACQ+∠ACP=180°.
∴P,C,Q三点在同一条直线上.
(2)PA=PB+PC.
理由如下:如答图2 所示,把△ABP 绕点A 按逆时针方向旋转到△ACQ.
∴P,C,Q三点在同一条直线上,∠BAP=∠CAQ,AP=AQ,PB=CQ.
即∠BAP+∠PAC=60°,
∴∠PAC+∠CAQ=60°,即∠PAQ=60°.
∴△APQ为等边三角形.∴PQ=PA.
∴PA=PC+CQ=PC+PB.
(3)(2)中的结论不成立.
23.(1)6πcm 4πcm6cm
②设MN所在圆的半径为r,所对的圆心角度数为n°,则
解得 r=12.
解得n=60.
所在圆的半径r为12cm,它所对的圆心角的度数为60°.
(2)如答图所示,连结EF,延长 EM,FN交于点O,设RS与EF交于点 P,OP 交ZX 于点Q.
∵∠MON=60°,
∴△MON 和△EOF 是等边三角形,
∴EF=12+6=18,
∵OQ⊥MN,MQ=QN,∴∠QON=30°.∴OQ=6
∴长方形的宽为(
设正方形边长为x(cm).
∵EF=18,∴BE=BF=9
在 Rt△AOE 中,
即 ,解得
∴正方形边长为
1.在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,D是AB 边的中点,以点C为圆心、2.4cm为半径作圆,则点 D与⊙C的位置关系是( ).
A.点 D 在⊙C上 B.点 D 在⊙C外 C.点 D 在⊙C内 D.不能确定
2.如图所示,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( ).
A.40° B.50° C.80° D.100°
3.如图所示,四边形ABCD内接于⊙O,AB经过圆心,∠B=3∠BAC,则∠ADC的度数为( ).
A.100° B.112.5° C.120° D.135°
4.运用图形变化的方法研究下列问题:如图所示,AB是⊙O 的直径,CD,EF 是⊙O的弦,且AB∥CD∥EF,AB=10,CD=6,EF=8,则图中阴影部分的面积是( ).
B.10π C.24+4π D.24+5π
5.如图所示,在⊙O中,半径OC⊥弦AB,垂足为D,且AB=8,OC=5,则CD的长为( ).
A.3 B.2.5 C.2 D.1
6.观察下列图片及相应推理,其中正确的是( ).
∵∠AOB=∠A'OB', ∵AD=BC, 的度数为40°, ∵MN 垂直平分AD,
∴AB=CD. ∴∠AOB=80°.
7.如图所示,正六边形硬纸片ABCDEF 在桌面上由图1的起始位置沿直线不滑行地翻滚一周后到图 2位置.若正六边形的边长为2cm,则正六边形的中心O运动的路程为( ).
A.πcm B.2πcm
C.3πcm D.4πcm
8.如图所示,在⊙O中,AB 为直径,∠AOC=80°,D为弦AC 的中点,E为 上任意一点,则∠CED 的度数可能是( ).
A.10° B.20° C.30° D.40°
9.如图所示,MN是半径为1的⊙O的直径,点 A 在⊙O上,∠AMN=30°,B是. 的中点. P是直径MN 上一动点,则 PA+PB 的最小值为( ).
A. B.1 C.2
10.如图1所示为一张圆形纸片,小芳对其进行了如下连续操作:将纸片左右对折,折痕为AB,如图2所示;将纸片上下折叠,使A,B两点重合,折痕CD与AB 相交于点 M,如图3所示;将纸片沿 EF折叠,使B,M两点重合,折痕EF与AB 相交于点 N,如图4所示;连结AE,AF,如图5所示.经过以上操作,小芳得到了以下结论:①CD∥EF;②四边形 MEBF 是菱形;③△AEF是等边三角形;( 其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
11.一条弦分圆周为5:7,这条弦所对的圆周角为 .
12.如图所示,正五边形 ABCDE 内接于⊙O,P,Q分别是边AB,BC上的点,且BP=CQ,则∠POQ 的度数为 .
13.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则该小圆孔的宽口AB的长为 mm.
14.在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y= kx-3k+4与⊙O交于B,C两点,则弦 BC 的长的最小值为 .
15.如图所示,在扇形 AOB中,∠AOB=90°,C是. 上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点 D,E.若DE=1,则扇形 AOB的面积为 .
16.正方形和圆都是人们比较喜欢的图形,给人以美感.某校数学兴趣小组在学习中发现:
(1)如图1所示,研究在以AB为直径的半圆中,裁剪出面积最大的正方形 CDEF时惊喜地发现,点C和点 F 其实分别是线段AF 和BC的黄金分割点.如果设圆的半径为r,那么此时正方形的边长(
(2)如图2所示,如果在半径为r的半圆中裁剪出两个同样大小且分别面积最大的正方形的边长( .如图3所示,并列n个正方形时的边长(
(3)如图4所示,当n=9时,我们还可以在第一层的上面再裁剪出同样大小的正方形,也可以再在第二层的上面再裁剪出第三层同样大小的正方形,则最多可以裁剪到第 层.
17.如图所示,在扇形AOB中,∠AOB=90°,正方形CDEF 的顶点C是 的中点,点 D在OB上,点E在OB的延长线上,当正方形CDEF 的边长为2 时,求阴影部分的面积.
18.如图所示,在平面直角坐标系中,直线l经过原点O,且与x轴正半轴的夹角为 点M在x轴上,⊙M半径为2,⊙M 与直线l相交于A,B两点,若 为等腰直角三角形,求点 M 的坐标.
19.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.若桥跨度AB约为40m,主拱高CD约10m.
(1)如图1所示,请通过尺规作图找到桥弧所在圆的圆心O(保留作图痕迹).
(2)如图2所示,求桥弧AB 所在圆的半径R.
20.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O交BC 于点D,延长CA交⊙O于点E,连结ED交AB 于点 F.
(1)求证:△CDE是等腰三角形.
(2)当 时,求 的值.
21.如图1所示,正方形ABCD内接于⊙O,E为上任意一点,连结DE,AE.
(1)求∠AED的度数.
(2)如图2所示,过点B作BF∥DE交⊙O于点 F,连结AF,AF=1,AE=4,求 DE的长.
22.已知⊙O中,AB=AC,P是 所对弧上一动点,连结 PB,PA.
(1)如图1所示,把 绕点A 按逆时针方向旋转到 求证:P,C,Q三点在同一条直线上.
(2)如图2所示,连结 PC,若 试探究 PA,PB,PC之间的关系,并说明理由.
(3)若∠BAC=120°,(2)中的结论是否成立 若成立,请证明;若不成立,请直接写出它们之间的数量关系,不需证明.
23.某班学习小组对无盖的纸杯进行制作与探究,所要制作的纸杯如图1所示,规格要求:杯口直径AB=6cm,杯底直径CD=4cm,杯壁母线AC=BD=6cm.请你和他们一起解决下列问题:
(1)小顾同学先画出了纸杯的侧面展开示意图(如图2中实线部分,忽略拼接部分),得到图形是圆环的一部分.
①图2中 的长为________,. 的长为___________,ME=NF=_______
②要想准确画出纸杯侧面的设计图,需要确定 所在圆的圆心O,如图2所示.小顾同学发现 之间存在以下关系 请你帮她证明这一结论.
③根据②中的结论,求 所在圆的半径r 及它所对的圆心角的度数n°.
(2)小顾同学计划利用矩形、正方形纸各一张,分别按如图3、图4所示的方式剪出这个纸杯的侧面,求矩形纸片的长和宽以及正方形纸片的边长.
1. B 2. D 3. B 4. A 5. C 6. B 7. D
8. C 【解析】如答图所示,连结OD,OE,BC.∵OC=OA,∴△OAC 是等腰三角形.∵D为弦AC 的中点,∴∠AOC=80°.
∴∠DOC=40°,∠BOC=100°.设∠BOE=x,则. +40°.
∵OC=OE,∠COE=100°-x,
∴∠OED<20°+ x.∴∠CED=∠OEC-∠OED>
中小学教育资源及组卷应用平台
∵∠CED<∠ABC=40°,∴20°<∠CED<40°.
故选 C.
9. A 10. D
11.75°或105° 12.72° 13.8 14.24 15.π/2
16.(1) , (2) , =,((3)5
17.如答图所示,连结OC.∵在扇形 AOB 中,∠AOB=90°,正方形 CDEF 的顶点C是AB的中点,
18.如答图所示,过点 M作MC⊥l于点C.
∵△MAB是等腰直角三角形,∴MA=MB.
∴∠BAM=∠ABM=45°.
∵MC⊥直线 l,
∴∠BAM=∠CMA=45°.∴AC=CM.
在Rt△ACM中,∵AC +CM =AM ,
即
在 Rt△OCM中,∠COM=30°,
根据对称性,在负半轴的点M(-2 ,0)也满足条件.
∴点 M 的坐标为(2 ,0)或(
19.(1)如答图所示.
(2)由(1)中的作图可知:△AOD为直角三角形,D是AB的中点.
∵CD=10m,∴OD=(R-10)m.
在 Rt△AOD中,由勾股定理得( 即 ,解得R=25.
∴桥弧 AB所在圆的半径R 为25m.
20.(1)∵AB=AC,∴∠ABC=∠C.
∵AD=AD,∴∠AED=∠ABC.
∴∠C=∠AED.∴△CDE是等腰三角形.
(2)如答图所示,连结AD,过点 D作DH⊥AE于点 H.
设
∵AB是直径,∴∠ADC=90°.
21.(1)如答图1 所示,连结OA,OD.
∵四边形ABCD是正方形,∴∠AOD=90°.
(2)如答图2所示,连结CF,CE,CA,BD,过点 D 作DH⊥AE 于点 H.
∵BF∥DE,∴∠FBD=∠EDB.
∵四边形ABCD是正方形,∴AB∥CD.
∴∠ABD=∠CDB.∴∠ABF=∠CDE.
∵∠CFA=∠AEC=90°,∴∠DEC=∠AFB=135°.
∵CD=AB,∴△CDE≌△ABF.∴CE=AF=1.
∵∠DHE=90°,∴∠HDE=∠HED=45°.
∴DH=HE.
设 DH=EH=x.
在 Rt△ADH 中,
解得 或
或
22.(1)如答图1所示,连结 PC.
∵把△ABP 绕点A 按逆时针方向旋转到△ACQ,
∴∠ABP=∠ACQ.
∵四边形ABPC为⊙O的内接四边形,
∴∠ABP+∠ACP=180°.∴∠ACQ+∠ACP=180°.
∴P,C,Q三点在同一条直线上.
(2)PA=PB+PC.
理由如下:如答图2 所示,把△ABP 绕点A 按逆时针方向旋转到△ACQ.
∴P,C,Q三点在同一条直线上,∠BAP=∠CAQ,AP=AQ,PB=CQ.
即∠BAP+∠PAC=60°,
∴∠PAC+∠CAQ=60°,即∠PAQ=60°.
∴△APQ为等边三角形.∴PQ=PA.
∴PA=PC+CQ=PC+PB.
(3)(2)中的结论不成立.
23.(1)6πcm 4πcm6cm
②设MN所在圆的半径为r,所对的圆心角度数为n°,则
解得 r=12.
解得n=60.
所在圆的半径r为12cm,它所对的圆心角的度数为60°.
(2)如答图所示,连结EF,延长 EM,FN交于点O,设RS与EF交于点 P,OP 交ZX 于点Q.
∵∠MON=60°,
∴△MON 和△EOF 是等边三角形,
∴EF=12+6=18,
∵OQ⊥MN,MQ=QN,∴∠QON=30°.∴OQ=6
∴长方形的宽为(
设正方形边长为x(cm).
∵EF=18,∴BE=BF=9
在 Rt△AOE 中,
即 ,解得
∴正方形边长为
同课章节目录
