专题复习二 与圆有关的角 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 专题复习二 与圆有关的角 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 386.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 21:46:37 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习二 与圆有关的角
1.如图所示,AB 是⊙O的一条弦,且OD⊥AB 于点 C,BD所对的圆周角∠DEB=35°,则∠AOD 的度数是( ).
A.35° B.55°
C.70° D.110°
2.如图所示,在⊙O中,O到AB的距离 则弦AB 所对圆心角的度数为( ).
A.60° B.90° C.120° D.150°
3.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O分别交 BC,AC 于点 D,E,则下列判断:①BD=CD;②BD=DE;③AE=DE;④△ABC为锐角三角形.其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,⊙O的圆心O在正方形网格的格点上,A,B两点在⊙O上,并且也在格点上,C为⊙O上一点,则∠ACB 的度数为 .
5.如图所示, ,AD为⊙O的弦,若∠BAD=50°,则∠AED的度数为 .
6.如图所示,⊙O是△ABC的外接圆, 点 D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE.
(2)如果点G 在线段DC 上(不与点 D 重合),且AG=AD,求证:四边形 AGCE 是平行四边形.
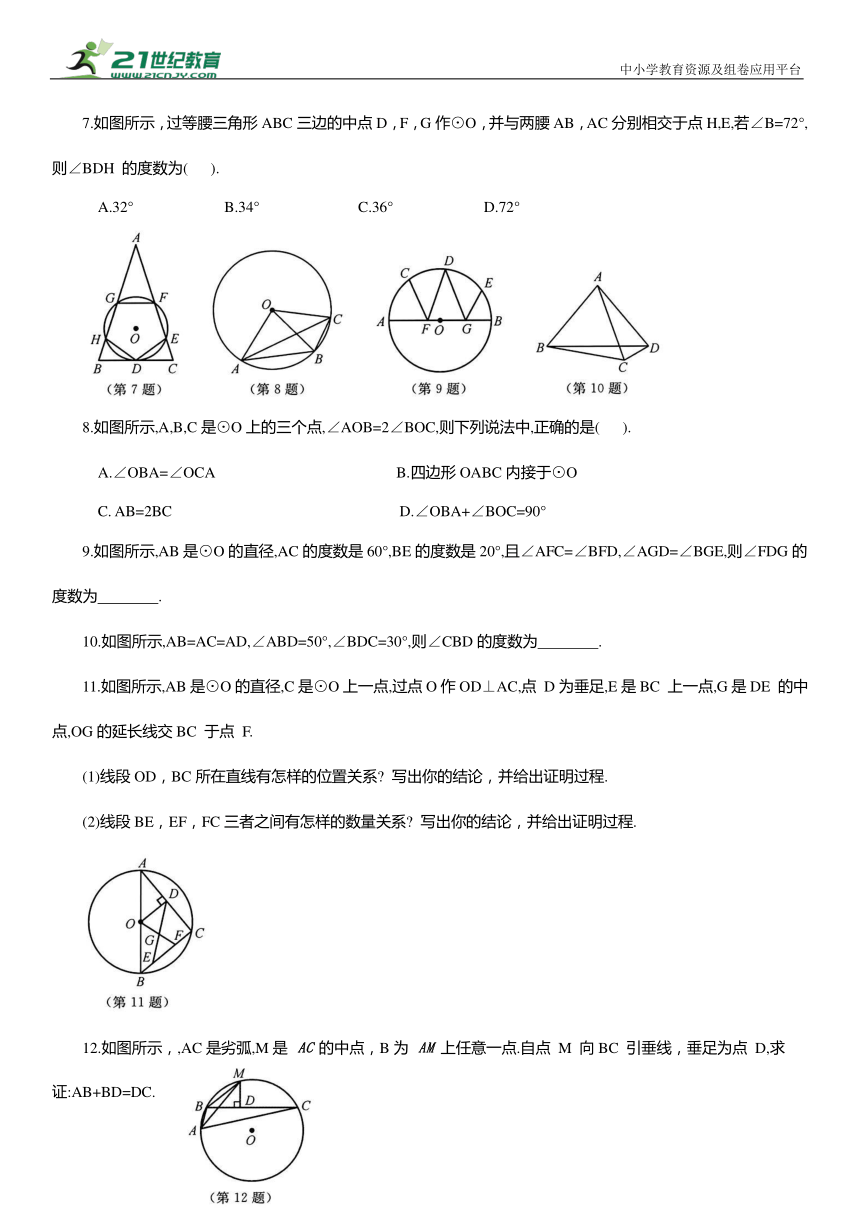
7.如图所示,过等腰三角形ABC三边的中点D,F,G作⊙O,并与两腰AB,AC分别相交于点H,E,若∠B=72°,则∠BDH 的度数为( ).
A.32° B.34° C.36° D.72°
8.如图所示,A,B,C是⊙O上的三个点,∠AOB=2∠BOC,则下列说法中,正确的是( ).
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C. AB=2BC D.∠OBA+∠BOC=90°
9.如图所示,AB是⊙O的直径,AC的度数是60°,BE的度数是20°,且∠AFC=∠BFD,∠AGD=∠BGE,则∠FDG的度数为 .
10.如图所示,AB=AC=AD,∠ABD=50°,∠BDC=30°,则∠CBD的度数为 .
11.如图所示,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AC,点 D为垂足,E是BC 上一点,G是DE 的中点,OG的延长线交BC 于点 F.
(1)线段OD,BC所在直线有怎样的位置关系 写出你的结论,并给出证明过程.
(2)线段BE,EF,FC三者之间有怎样的数量关系 写出你的结论,并给出证明过程.
12.如图所示,,AC是劣弧,M是 的中点,B为 上任意一点.自点 M 向BC 引垂线,垂足为点 D,求证:AB+BD=DC.
13.如图所示,四边形 ABCD 内接于⊙O,连结 BD.若 ∠BDC=50°,则∠ADC的度数是( ).
A.125° B.130°
C.135° D.140°
14.如图所示,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC 弦BM平分∠ABC交AC 于点D,连结MA,MC.
(1)求⊙O半径的长.
(2)求证:AB+BC=BM.
15.如图1所示,已知AB 是⊙O的直径,C 是 上的一个动点(点C 与点 A,B不重合),连结AC,D是 的中点,作弦DE⊥AB,垂足为点 F.
(1)若点C和点E 不重合,连结BC,CE和EB,当△BCE是等腰三角形时,求∠CAB的度数.
(2)若点C和点E 重合,如图2所示,试探索 AB与AC 的数量关系并说明理由.
专题复习二 与圆有关的角
1. C 2. C 3. C 4.45° 5.75°
6.(1)在⊙O中,∵AB=AC,∴AB=AC.
∴∠B=∠ACB.
∵AE∥BC,∴∠EAC=∠ACB.∴∠B=∠EAC.
在△ABD和△CAE中,
∴△ABD≌△CAE(SAS).
∴AD=CE.
(2)如答图所示,连结 AO 并延长,交边 BC于点 H.
OA为半径,
∴AH⊥BC.∴BH=CH.
∵AD=AG,∴DH=HG.
∴BH-DH=CH-GH,即 BD=CG.
∵BD=AE,∴CG=AE.
∵CG∥AE,∴四边形 AGCE 是平行四边形.
7. C 8. D 9.50° 10.10°
11.(1)OD∥BC.
证明:∵AB是⊙O直径,C是⊙O上一点,
∴∠ACB=90°,即 BC⊥AC.
∵OD⊥AC,∴OD∥BC.
(2)EF=BE+FC.
证明:∵OD⊥AC,∴AD=DC.
∵O为AB 的中点,∴OD 是△ABC的中位线.
∴BC=2OD.
∵∠ODG=∠FEG,DG=EG,∠GOD=∠GFE,
∴△ODG≌△FEG.∴OD=EF.
∴BC=BE+EF+FC=2OD=2EF.∴EF=BE+FC.
12.如答图所示,在 CD 上取点 N,使 CN=AB,连结CM,MN.
∵M是AC的中点,
∴AM=CM.
∵AB = CN,∠BAM= ∠BCM,AM=CM,
∴△ABM≌△CNM.∴BM=MN.
∵MD⊥BN,∴BD=DN.
∴AB+BD=CN+DN=CD.
13. B
14.(1)如答图1所示,连结OA,OC,过点O作OH⊥AC于点 H.
∵∠ABC=120°,∴∠AMC=180°-∠ABC=60°.
∴∠AOC=2∠AMC=120°.∴∠AOH= ∠AOC=
∴⊙O的半径为2.
(2)如答图2所示,在 BM上截取BE=BC,连结CE.
∵∠MBC=60°,BE=BC,∴△EBC是等边三角形.
∴CE=CB=BE,∠BCE=60°.
∴∠BCD+∠DCE=60°.
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°.
∴∠CAM=∠CBM=60°,∠ACM=∠ABM=60°.
∴△ACM是等边三角形.∴AC=CM.
∵∠ACM=60°,∴∠ECM+∠DCE=60°.
∴∠ECM=∠BCD.
∴△ACB≌△MCE.∴AB=ME.
∵ME+EB=BM,∴AB+BC=BM.
15.(1)连结OC,当△BCE是等腰三角形时,分两种情况:
①当CE=BC时,如答图1所示,.
设 的度数为x°,则CE的度数为x°,BE的度数为2x°.
∵DE⊥AB,AB为直径,
的度数为3x°.
∵D是ABC的中点, 的度数为6x°.
∴AB的度数为
又∵AB的度数为180°,∴5x=180,解得x=36.
②当CE=BE时,如答图2 所示..
设的度数为x°,则CE的度数为x°.
∵DE⊥AB,AB为直径,.
∴CD的度数为3x°.
∵D是ABC的中点,∴ABC的度数为6x°.
∴AB的度数为4x°.
又∵AB的的度数为180°,∴4x=180,解得x=45.
∴BC的度数为
综上所述,当△BCE 是等腰三角形时,∠CAB的度数是18°或45°.
∵D是ABC的中点,
且其度数为2x°.∴AB的度数为3x°.
∵AB的度数为180°,∴3x=180,解得x=60.
∵AB为⊙O的直径,.
专题复习二 与圆有关的角
1.如图所示,AB 是⊙O的一条弦,且OD⊥AB 于点 C,BD所对的圆周角∠DEB=35°,则∠AOD 的度数是( ).
A.35° B.55°
C.70° D.110°
2.如图所示,在⊙O中,O到AB的距离 则弦AB 所对圆心角的度数为( ).
A.60° B.90° C.120° D.150°
3.如图所示,在△ABC中,AB=AC,以AB为直径的⊙O分别交 BC,AC 于点 D,E,则下列判断:①BD=CD;②BD=DE;③AE=DE;④△ABC为锐角三角形.其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,⊙O的圆心O在正方形网格的格点上,A,B两点在⊙O上,并且也在格点上,C为⊙O上一点,则∠ACB 的度数为 .
5.如图所示, ,AD为⊙O的弦,若∠BAD=50°,则∠AED的度数为 .
6.如图所示,⊙O是△ABC的外接圆, 点 D在边BC上,AE∥BC,AE=BD.
(1)求证:AD=CE.
(2)如果点G 在线段DC 上(不与点 D 重合),且AG=AD,求证:四边形 AGCE 是平行四边形.
7.如图所示,过等腰三角形ABC三边的中点D,F,G作⊙O,并与两腰AB,AC分别相交于点H,E,若∠B=72°,则∠BDH 的度数为( ).
A.32° B.34° C.36° D.72°
8.如图所示,A,B,C是⊙O上的三个点,∠AOB=2∠BOC,则下列说法中,正确的是( ).
A.∠OBA=∠OCA B.四边形OABC内接于⊙O
C. AB=2BC D.∠OBA+∠BOC=90°
9.如图所示,AB是⊙O的直径,AC的度数是60°,BE的度数是20°,且∠AFC=∠BFD,∠AGD=∠BGE,则∠FDG的度数为 .
10.如图所示,AB=AC=AD,∠ABD=50°,∠BDC=30°,则∠CBD的度数为 .
11.如图所示,AB是⊙O的直径,C是⊙O上一点,过点O作OD⊥AC,点 D为垂足,E是BC 上一点,G是DE 的中点,OG的延长线交BC 于点 F.
(1)线段OD,BC所在直线有怎样的位置关系 写出你的结论,并给出证明过程.
(2)线段BE,EF,FC三者之间有怎样的数量关系 写出你的结论,并给出证明过程.
12.如图所示,,AC是劣弧,M是 的中点,B为 上任意一点.自点 M 向BC 引垂线,垂足为点 D,求证:AB+BD=DC.
13.如图所示,四边形 ABCD 内接于⊙O,连结 BD.若 ∠BDC=50°,则∠ADC的度数是( ).
A.125° B.130°
C.135° D.140°
14.如图所示,在⊙O中,B是⊙O上的一点,∠ABC=120°,弦AC 弦BM平分∠ABC交AC 于点D,连结MA,MC.
(1)求⊙O半径的长.
(2)求证:AB+BC=BM.
15.如图1所示,已知AB 是⊙O的直径,C 是 上的一个动点(点C 与点 A,B不重合),连结AC,D是 的中点,作弦DE⊥AB,垂足为点 F.
(1)若点C和点E 不重合,连结BC,CE和EB,当△BCE是等腰三角形时,求∠CAB的度数.
(2)若点C和点E 重合,如图2所示,试探索 AB与AC 的数量关系并说明理由.
专题复习二 与圆有关的角
1. C 2. C 3. C 4.45° 5.75°
6.(1)在⊙O中,∵AB=AC,∴AB=AC.
∴∠B=∠ACB.
∵AE∥BC,∴∠EAC=∠ACB.∴∠B=∠EAC.
在△ABD和△CAE中,
∴△ABD≌△CAE(SAS).
∴AD=CE.
(2)如答图所示,连结 AO 并延长,交边 BC于点 H.
OA为半径,
∴AH⊥BC.∴BH=CH.
∵AD=AG,∴DH=HG.
∴BH-DH=CH-GH,即 BD=CG.
∵BD=AE,∴CG=AE.
∵CG∥AE,∴四边形 AGCE 是平行四边形.
7. C 8. D 9.50° 10.10°
11.(1)OD∥BC.
证明:∵AB是⊙O直径,C是⊙O上一点,
∴∠ACB=90°,即 BC⊥AC.
∵OD⊥AC,∴OD∥BC.
(2)EF=BE+FC.
证明:∵OD⊥AC,∴AD=DC.
∵O为AB 的中点,∴OD 是△ABC的中位线.
∴BC=2OD.
∵∠ODG=∠FEG,DG=EG,∠GOD=∠GFE,
∴△ODG≌△FEG.∴OD=EF.
∴BC=BE+EF+FC=2OD=2EF.∴EF=BE+FC.
12.如答图所示,在 CD 上取点 N,使 CN=AB,连结CM,MN.
∵M是AC的中点,
∴AM=CM.
∵AB = CN,∠BAM= ∠BCM,AM=CM,
∴△ABM≌△CNM.∴BM=MN.
∵MD⊥BN,∴BD=DN.
∴AB+BD=CN+DN=CD.
13. B
14.(1)如答图1所示,连结OA,OC,过点O作OH⊥AC于点 H.
∵∠ABC=120°,∴∠AMC=180°-∠ABC=60°.
∴∠AOC=2∠AMC=120°.∴∠AOH= ∠AOC=
∴⊙O的半径为2.
(2)如答图2所示,在 BM上截取BE=BC,连结CE.
∵∠MBC=60°,BE=BC,∴△EBC是等边三角形.
∴CE=CB=BE,∠BCE=60°.
∴∠BCD+∠DCE=60°.
∵∠ABC=120°,BM平分∠ABC,
∴∠ABM=∠CBM=60°.
∴∠CAM=∠CBM=60°,∠ACM=∠ABM=60°.
∴△ACM是等边三角形.∴AC=CM.
∵∠ACM=60°,∴∠ECM+∠DCE=60°.
∴∠ECM=∠BCD.
∴△ACB≌△MCE.∴AB=ME.
∵ME+EB=BM,∴AB+BC=BM.
15.(1)连结OC,当△BCE是等腰三角形时,分两种情况:
①当CE=BC时,如答图1所示,.
设 的度数为x°,则CE的度数为x°,BE的度数为2x°.
∵DE⊥AB,AB为直径,
的度数为3x°.
∵D是ABC的中点, 的度数为6x°.
∴AB的度数为
又∵AB的度数为180°,∴5x=180,解得x=36.
②当CE=BE时,如答图2 所示..
设的度数为x°,则CE的度数为x°.
∵DE⊥AB,AB为直径,.
∴CD的度数为3x°.
∵D是ABC的中点,∴ABC的度数为6x°.
∴AB的度数为4x°.
又∵AB的的度数为180°,∴4x=180,解得x=45.
∴BC的度数为
综上所述,当△BCE 是等腰三角形时,∠CAB的度数是18°或45°.
∵D是ABC的中点,
且其度数为2x°.∴AB的度数为3x°.
∵AB的度数为180°,∴3x=180,解得x=60.
∵AB为⊙O的直径,.
同课章节目录
