专题复习三 运动路径及不规则图形面积的计算 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 专题复习三 运动路径及不规则图形面积的计算 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 403.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 21:59:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习三 运动路径及不规则图形面积的计算
基础巩固
1.如图所示的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从点 A 到点 B,甲虫沿 路线爬行,乙虫沿 路线爬行,则下列结论中,正确的是( ).
A.甲先到点 B B.乙先到点 B
C.甲、乙同时到点 B D.无法确定
2.如图所示,Rt△AB'C'是 Rt△ABC以点A 为中心按逆时针方向旋转90°而得到的,其中AB=1,BC=2,则旋转过程中CC的长为( ).
C.5π D.
如图所示,⊙O的半径为2,AB,CD是互相垂直的两条直径,P 是⊙O上任意一点(P与点A,B,C,D不重合),过点 P作PM⊥AB于点M,PN⊥CD于点N,Q是MN 的中点.当点 P 沿着圆周转过45°时,点Q 走过的路径
长为( ).
A.π/4 B.π/2 C.π/6 D.π/3
4.如图所示,分别以五边形 ABCDE的顶点为圆心、1为半径作圆,则图中阴影部分的面积之和为( ).
B.3π D.2π
5.如图1所示为以AB为直径的半圆形纸片,AB=6cm,沿着垂直于AB 的半径OC 剪开,将扇形 AOC 沿AB 方向平移至扇形A'O'C',如图2所示.其中O'是OB 的中点,O'C'交. 于点F,则的长为 cm.
6.如图所示,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM,ON分别与⊙O交于点E,F,与正方形ABCD的边交于点G,H,则阴影部分的面积S= .
7.如图所示,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A 按逆时针方向旋转90°得到线段AC.
(1)请你用尺规在所给的网格中画出线段AC 及点B 经过的路径.
(2)若将此网格放在一平面直角坐标系中,已知点 A 的坐标为(1,3),点 B 的坐标为(-2,-1),则点 C的坐标为 .
(3)在线段AB 旋转到线段AC 的过程中,线段 AB 扫过的区域的面积为 .
8.如图所示,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的⊙O交BC于点D,且
(1)求证:AB为⊙O的直径.
(2)若AB=8,∠BAC=45°,求图中阴影部分的面积.
能力提升
9.如图所示,在平面直角坐标系中放置一个边长为1的正方形ABCD,将正方形 ABCD 沿x轴的正方向无滑动地在x轴上滚动,当点 A 离开原点后第一次落在x轴上时,点A 运动的路径线与x 轴围成的图形面积为( ).
C.π+1
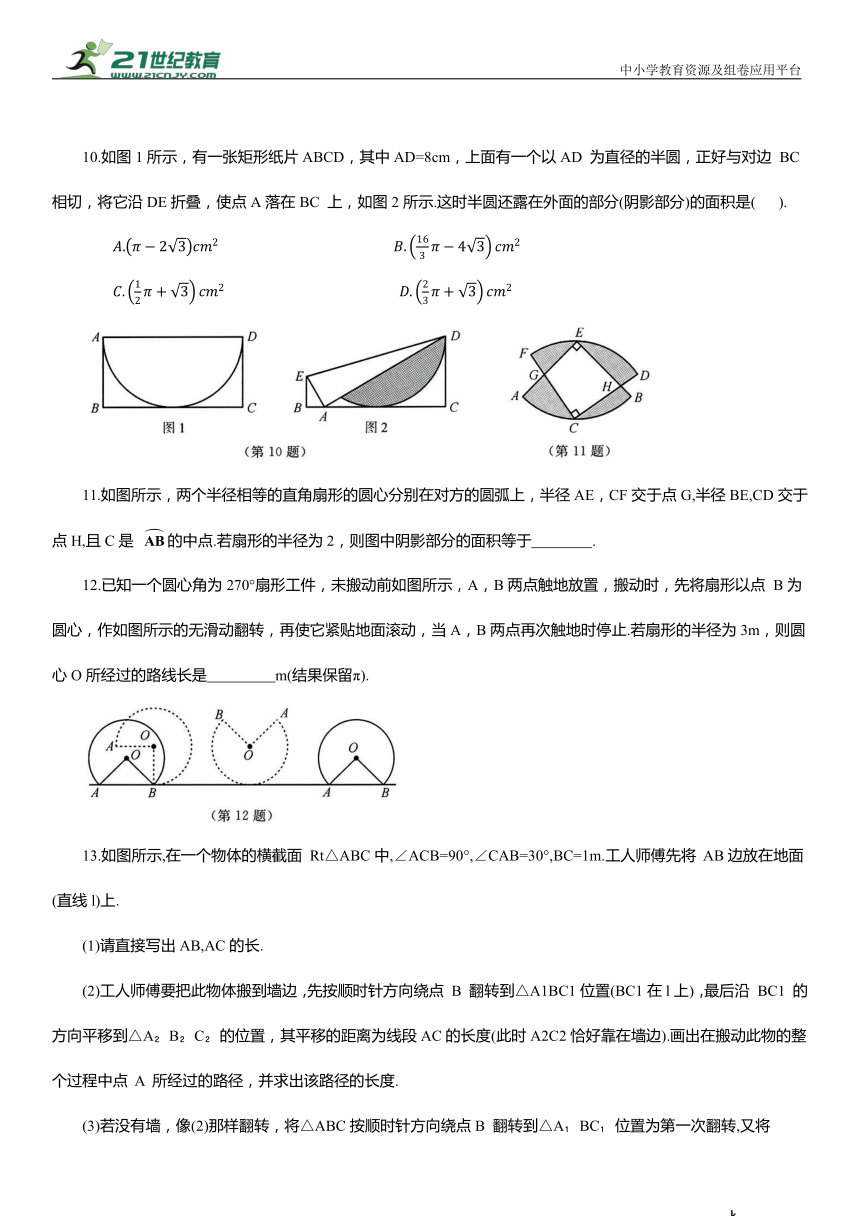
10.如图1所示,有一张矩形纸片ABCD,其中AD=8cm,上面有一个以AD 为直径的半圆,正好与对边 BC相切,将它沿DE折叠,使点A落在BC 上,如图2所示.这时半圆还露在外面的部分(阴影部分)的面积是( ).
11.如图所示,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE,CF交于点G,半径BE,CD交于点H,且C是 的中点.若扇形的半径为2,则图中阴影部分的面积等于 .
12.已知一个圆心角为270°扇形工件,未搬动前如图所示,A,B两点触地放置,搬动时,先将扇形以点 B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止.若扇形的半径为3m,则圆心O所经过的路线长是 m(结果保留π).
13.如图所示,在一个物体的横截面 Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=1m.工人师傅先将 AB边放在地面(直线l)上.
(1)请直接写出AB,AC的长.
(2)工人师傅要把此物体搬到墙边,先按顺时针方向绕点 B 翻转到△A1BC1位置(BC1在l上),最后沿 BC1 的方向平移到△A B C 的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).画出在搬动此物的整个过程中点 A 所经过的路径,并求出该路径的长度.
(3)若没有墙,像(2)那样翻转,将△ABC按顺时针方向绕点B 翻转到△A BC 位置为第一次翻转,又将△A BC 按顺时针方向绕点 C 翻转到△A B C (A C 在l上)为第二次翻转,求两次翻转此物的整个过程中点 A 经过路径的长度.
夯实演练
14.如图所示,已知C,D是以AB 为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( ).
15.如图所示为由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点 D按下列步骤移动:第一步:点D 绕点A 按顺时针方向旋转180°得到点 D1;第二步:点 D1绕点B 按顺时针方向旋转90°得到点 D2;第三步:点 D2绕点 C按顺时针方向旋转90°回到点 D.
(1)请用圆规画出点. 经过的路径.
(2)所画图形是 对称图形.
(3)求所画图形的周长(结果保留π).
16.如图所示,正方形ABCD的边长为1,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画圆弧,求图中阴影部分的面积.
专题复习三 运动路径及不规则图形面积的计算
1. C 2. A 3. A 4. C 5.π 6.π-2
7.(1)图略(2)(5,0)
8.(1)如答图所示,连结AD.
∵BD=DE,∴∠BAD=∠CAD.
又∵AB=AC,∴AD⊥BC.
∴AB为⊙O的直径.
(2)连结OE.
∵∠BAC=45°,∴∠BOE=90°.
∴∠AOE=90°.
∵AB为⊙O的直径,∴∠AEB=90°.
∴阴影部分的面积为
9. C 10. B 11.2π-4 12.6π
13.(1)AB=2m,AC= m.
(2)如答图所示,点A 经过的路径为
∴点A 所经过的路径长为
(3)点A 经过的路径为
∴点 A 经过的路径长度为
14. A 【解析】如答图所示,连结CD,OC,OD.
∵C,D是以AB 为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD.
又∵OA=OC=OD,∴△OAC,△OCD均是等边三角形.
∴∠AOC=∠OCD.∴CD∥AB.∴S△ACD=S△OCD.
∵弧CD 的长为 解得 r=1.
故选 A.
15.(1)点. 经过的路径如答图所示.
(2)轴
(3)周长为
16.如答图所示,设正方形的各部分不规则图形的面积分别为x,y,z. S正方形ABCD =x+4y+4z 可解得
∴图中阴影部分的面积为
专题复习三 运动路径及不规则图形面积的计算
基础巩固
1.如图所示的五个半圆,邻近的两半圆相切,两只小虫同时出发,以相同的速度从点 A 到点 B,甲虫沿 路线爬行,乙虫沿 路线爬行,则下列结论中,正确的是( ).
A.甲先到点 B B.乙先到点 B
C.甲、乙同时到点 B D.无法确定
2.如图所示,Rt△AB'C'是 Rt△ABC以点A 为中心按逆时针方向旋转90°而得到的,其中AB=1,BC=2,则旋转过程中CC的长为( ).
C.5π D.
如图所示,⊙O的半径为2,AB,CD是互相垂直的两条直径,P 是⊙O上任意一点(P与点A,B,C,D不重合),过点 P作PM⊥AB于点M,PN⊥CD于点N,Q是MN 的中点.当点 P 沿着圆周转过45°时,点Q 走过的路径
长为( ).
A.π/4 B.π/2 C.π/6 D.π/3
4.如图所示,分别以五边形 ABCDE的顶点为圆心、1为半径作圆,则图中阴影部分的面积之和为( ).
B.3π D.2π
5.如图1所示为以AB为直径的半圆形纸片,AB=6cm,沿着垂直于AB 的半径OC 剪开,将扇形 AOC 沿AB 方向平移至扇形A'O'C',如图2所示.其中O'是OB 的中点,O'C'交. 于点F,则的长为 cm.
6.如图所示,正方形ABCD内接于⊙O,⊙O的半径为2,以圆心O为顶点作∠MON,使∠MON=90°,OM,ON分别与⊙O交于点E,F,与正方形ABCD的边交于点G,H,则阴影部分的面积S= .
7.如图所示,线段AB的端点在边长为1的正方形网格的格点上,现将线段AB绕点A 按逆时针方向旋转90°得到线段AC.
(1)请你用尺规在所给的网格中画出线段AC 及点B 经过的路径.
(2)若将此网格放在一平面直角坐标系中,已知点 A 的坐标为(1,3),点 B 的坐标为(-2,-1),则点 C的坐标为 .
(3)在线段AB 旋转到线段AC 的过程中,线段 AB 扫过的区域的面积为 .
8.如图所示,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的⊙O交BC于点D,且
(1)求证:AB为⊙O的直径.
(2)若AB=8,∠BAC=45°,求图中阴影部分的面积.
能力提升
9.如图所示,在平面直角坐标系中放置一个边长为1的正方形ABCD,将正方形 ABCD 沿x轴的正方向无滑动地在x轴上滚动,当点 A 离开原点后第一次落在x轴上时,点A 运动的路径线与x 轴围成的图形面积为( ).
C.π+1
10.如图1所示,有一张矩形纸片ABCD,其中AD=8cm,上面有一个以AD 为直径的半圆,正好与对边 BC相切,将它沿DE折叠,使点A落在BC 上,如图2所示.这时半圆还露在外面的部分(阴影部分)的面积是( ).
11.如图所示,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE,CF交于点G,半径BE,CD交于点H,且C是 的中点.若扇形的半径为2,则图中阴影部分的面积等于 .
12.已知一个圆心角为270°扇形工件,未搬动前如图所示,A,B两点触地放置,搬动时,先将扇形以点 B为圆心,作如图所示的无滑动翻转,再使它紧贴地面滚动,当A,B两点再次触地时停止.若扇形的半径为3m,则圆心O所经过的路线长是 m(结果保留π).
13.如图所示,在一个物体的横截面 Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=1m.工人师傅先将 AB边放在地面(直线l)上.
(1)请直接写出AB,AC的长.
(2)工人师傅要把此物体搬到墙边,先按顺时针方向绕点 B 翻转到△A1BC1位置(BC1在l上),最后沿 BC1 的方向平移到△A B C 的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).画出在搬动此物的整个过程中点 A 所经过的路径,并求出该路径的长度.
(3)若没有墙,像(2)那样翻转,将△ABC按顺时针方向绕点B 翻转到△A BC 位置为第一次翻转,又将△A BC 按顺时针方向绕点 C 翻转到△A B C (A C 在l上)为第二次翻转,求两次翻转此物的整个过程中点 A 经过路径的长度.
夯实演练
14.如图所示,已知C,D是以AB 为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( ).
15.如图所示为由边长为1的小正方形组成的8×4网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点 D按下列步骤移动:第一步:点D 绕点A 按顺时针方向旋转180°得到点 D1;第二步:点 D1绕点B 按顺时针方向旋转90°得到点 D2;第三步:点 D2绕点 C按顺时针方向旋转90°回到点 D.
(1)请用圆规画出点. 经过的路径.
(2)所画图形是 对称图形.
(3)求所画图形的周长(结果保留π).
16.如图所示,正方形ABCD的边长为1,分别以正方形的四个顶点为圆心,边长为半径,在正方形内画圆弧,求图中阴影部分的面积.
专题复习三 运动路径及不规则图形面积的计算
1. C 2. A 3. A 4. C 5.π 6.π-2
7.(1)图略(2)(5,0)
8.(1)如答图所示,连结AD.
∵BD=DE,∴∠BAD=∠CAD.
又∵AB=AC,∴AD⊥BC.
∴AB为⊙O的直径.
(2)连结OE.
∵∠BAC=45°,∴∠BOE=90°.
∴∠AOE=90°.
∵AB为⊙O的直径,∴∠AEB=90°.
∴阴影部分的面积为
9. C 10. B 11.2π-4 12.6π
13.(1)AB=2m,AC= m.
(2)如答图所示,点A 经过的路径为
∴点A 所经过的路径长为
(3)点A 经过的路径为
∴点 A 经过的路径长度为
14. A 【解析】如答图所示,连结CD,OC,OD.
∵C,D是以AB 为直径的半圆的三等分点,
∴∠AOC=∠COD=∠DOB=60°,AC=CD.
又∵OA=OC=OD,∴△OAC,△OCD均是等边三角形.
∴∠AOC=∠OCD.∴CD∥AB.∴S△ACD=S△OCD.
∵弧CD 的长为 解得 r=1.
故选 A.
15.(1)点. 经过的路径如答图所示.
(2)轴
(3)周长为
16.如答图所示,设正方形的各部分不规则图形的面积分别为x,y,z. S正方形ABCD =x+4y+4z 可解得
∴图中阴影部分的面积为
同课章节目录
