3.3 垂径定理(2)提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.3 垂径定理(2)提优训练(含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 348.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 21:56:12 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
3.3 垂径定理(2)
基础巩固
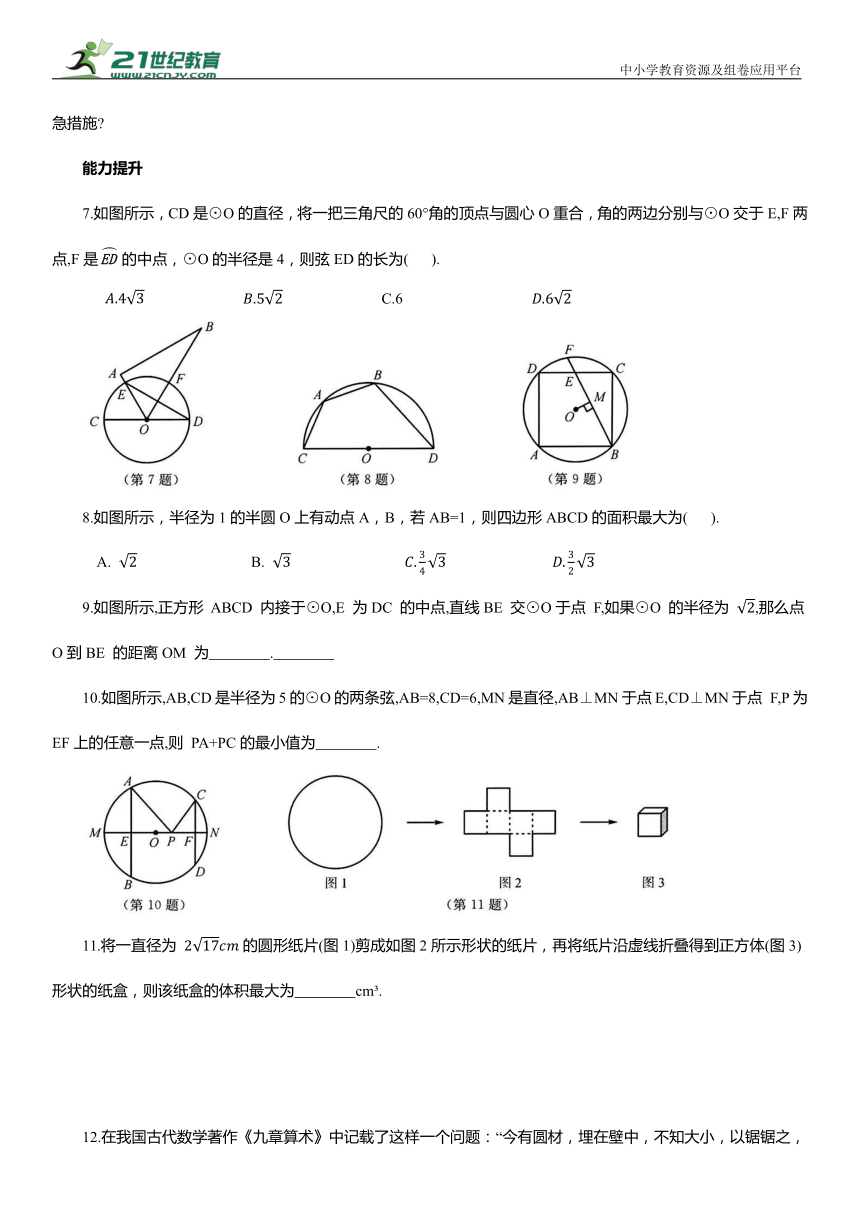
1.如图所示,在半径为13cm的圆形铁片上切下一块高为8cm 的弓形铁片,则弓形弦AB的长为( ).
A.10cm B.16cm C.24cm D.26cm
2.杭州市钱江新城有一处标志性建筑就是“日月同辉”,其中“日”指的是“杭州国际会议中心”,如图所示为它的主视图.已知这个球体的高度是85m,球的半径是50m,则杭州国际会议中心的占地面积是( ).
A.1275πm C.3825πm
3.如图所示,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点 D,E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为( ).
A.1cm B.2cm C.3cm D.4cm
4.如图所示,在⊙O中,AB,AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么⊙O的半径OA 的长为 .
5.如图1所示,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB 的距离为10cm,则该脸盆的半径为 cm.
6.如图所示,有一座圆弧形拱桥,它的跨度AB=60m,拱高 PD=18m.
(1)求该圆弧所在的圆的半径r的长.
(2)当洪水泛滥到跨度只有30m时,要采取紧急措施,若拱顶离水面只有4m,即PE=4m时,是否需要采取紧急措施
能力提升
7.如图所示,CD是⊙O的直径,将一把三角尺的60°角的顶点与圆心O重合,角的两边分别与⊙O交于E,F两点,F是的中点,⊙O的半径是4,则弦ED的长为( ).
C.6
8.如图所示,半径为1的半圆O上有动点A,B,若AB=1,则四边形ABCD的面积最大为( ).
A. B.
9.如图所示,正方形 ABCD 内接于⊙O,E 为DC 的中点,直线BE 交⊙O于点 F,如果⊙O 的半径为 ,那么点O到BE 的距离OM 为 .
10.如图所示,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点 F,P为EF上的任意一点,则 PA+PC的最小值为 .
11.将一直径为 的圆形纸片(图1)剪成如图2所示形状的纸片,再将纸片沿虚线折叠得到正方体(图3)形状的纸盒,则该纸盒的体积最大为 cm .
12.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”其大意如下:如图所示,AB为⊙O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB 的长.请你解答这个问题.
夯实演练
13.如图所示,一条公路的转弯处是一段圆弧点O是这段弧所在圆的圆心,AB=40m,C 是的中点,D是AB 的中点,且CD=10m,则该段弯路所在圆的半径为( ).
A.25m B.24m
C.30m D.60m
14.如图所示为一名同学从照片上剪切下来的海上日出时的画面,图上太阳与海平线交于A,B两点,他测得图上太阳的半径为10cm,AB=16cm.若从目前太阳所处位置到太阳完全跳出海平面的时间为16min,则图上太阳升起的速度为( ).
A.1.0 cm/ min B.0. 8cm / min C.1. 2cm / min D.1.4 cm/ min
15.如图所示,C是⊙O上. 的中点,弦AB=6cm,E为OC上任意一点,动点 F 从点A出发,以1cm/s的速度沿AB 方向向点 B 匀速运动,若 求 y关于动点F 的运动时间x(s)(0≤x≤6)的函数表达式.
3.3 垂径定理(2)
1. C 2. A 3. C 4.5cm 5.25
6.(1)如答图所示,连结OA.
由题意得
在 Rt△ADO中,由勾股定理得 解得r=34.
∴圆弧所在的圆的半径r的长为34m.
(2)连结OA'.易知OE=OP-PE=30(m),在 Rt△A'EO中,由勾股定理得. 即 解得 A'E=16.
∴不需要采取紧急措施.
7. A8. C 9. 10.7 11.8
12.如答图所示,连结OC.
∵弦CD⊥AB,AB为⊙O的直径,
∴E为CD 的中点.
又∵CD=10寸,
寸.
设OC=OA=x(寸),则AB=2x(寸),OE=(x-1)寸,由勾股定理得(
即 解得x=13,
∴AB=26寸,即直径AB的长为26寸.
13. A 14. A
15.如答图所示,延长 CO交AB 于点G.
∵C是ACB的的中点,
当0≤x≤3时,AF=x(cm),FG=(3-x)(cm),
当3
3.3 垂径定理(2)
基础巩固
1.如图所示,在半径为13cm的圆形铁片上切下一块高为8cm 的弓形铁片,则弓形弦AB的长为( ).
A.10cm B.16cm C.24cm D.26cm
2.杭州市钱江新城有一处标志性建筑就是“日月同辉”,其中“日”指的是“杭州国际会议中心”,如图所示为它的主视图.已知这个球体的高度是85m,球的半径是50m,则杭州国际会议中心的占地面积是( ).
A.1275πm C.3825πm
3.如图所示,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点 D,E,量出半径OC=5cm,弦DE=8cm,则直尺的宽度为( ).
A.1cm B.2cm C.3cm D.4cm
4.如图所示,在⊙O中,AB,AC是互相垂直的两条弦,OD⊥AB于点D,OE⊥AC于点E,且AB=8cm,AC=6cm,那么⊙O的半径OA 的长为 .
5.如图1所示,小敏利用课余时间制作了一个脸盆架,图2是它的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40cm,脸盆的最低点C到AB 的距离为10cm,则该脸盆的半径为 cm.
6.如图所示,有一座圆弧形拱桥,它的跨度AB=60m,拱高 PD=18m.
(1)求该圆弧所在的圆的半径r的长.
(2)当洪水泛滥到跨度只有30m时,要采取紧急措施,若拱顶离水面只有4m,即PE=4m时,是否需要采取紧急措施
能力提升
7.如图所示,CD是⊙O的直径,将一把三角尺的60°角的顶点与圆心O重合,角的两边分别与⊙O交于E,F两点,F是的中点,⊙O的半径是4,则弦ED的长为( ).
C.6
8.如图所示,半径为1的半圆O上有动点A,B,若AB=1,则四边形ABCD的面积最大为( ).
A. B.
9.如图所示,正方形 ABCD 内接于⊙O,E 为DC 的中点,直线BE 交⊙O于点 F,如果⊙O 的半径为 ,那么点O到BE 的距离OM 为 .
10.如图所示,AB,CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点 F,P为EF上的任意一点,则 PA+PC的最小值为 .
11.将一直径为 的圆形纸片(图1)剪成如图2所示形状的纸片,再将纸片沿虚线折叠得到正方体(图3)形状的纸盒,则该纸盒的体积最大为 cm .
12.在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”其大意如下:如图所示,AB为⊙O的直径,弦CD⊥AB于点E,AE=1寸,CD=10寸,求直径AB 的长.请你解答这个问题.
夯实演练
13.如图所示,一条公路的转弯处是一段圆弧点O是这段弧所在圆的圆心,AB=40m,C 是的中点,D是AB 的中点,且CD=10m,则该段弯路所在圆的半径为( ).
A.25m B.24m
C.30m D.60m
14.如图所示为一名同学从照片上剪切下来的海上日出时的画面,图上太阳与海平线交于A,B两点,他测得图上太阳的半径为10cm,AB=16cm.若从目前太阳所处位置到太阳完全跳出海平面的时间为16min,则图上太阳升起的速度为( ).
A.1.0 cm/ min B.0. 8cm / min C.1. 2cm / min D.1.4 cm/ min
15.如图所示,C是⊙O上. 的中点,弦AB=6cm,E为OC上任意一点,动点 F 从点A出发,以1cm/s的速度沿AB 方向向点 B 匀速运动,若 求 y关于动点F 的运动时间x(s)(0≤x≤6)的函数表达式.
3.3 垂径定理(2)
1. C 2. A 3. C 4.5cm 5.25
6.(1)如答图所示,连结OA.
由题意得
在 Rt△ADO中,由勾股定理得 解得r=34.
∴圆弧所在的圆的半径r的长为34m.
(2)连结OA'.易知OE=OP-PE=30(m),在 Rt△A'EO中,由勾股定理得. 即 解得 A'E=16.
∴不需要采取紧急措施.
7. A8. C 9. 10.7 11.8
12.如答图所示,连结OC.
∵弦CD⊥AB,AB为⊙O的直径,
∴E为CD 的中点.
又∵CD=10寸,
寸.
设OC=OA=x(寸),则AB=2x(寸),OE=(x-1)寸,由勾股定理得(
即 解得x=13,
∴AB=26寸,即直径AB的长为26寸.
13. A 14. A
15.如答图所示,延长 CO交AB 于点G.
∵C是ACB的的中点,
当0≤x≤3时,AF=x(cm),FG=(3-x)(cm),
当3
同课章节目录
