3.4 圆心角(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 3.4 圆心角(2) 提优训练(含答案)2024-2025学年浙教版九年级数学上册 | 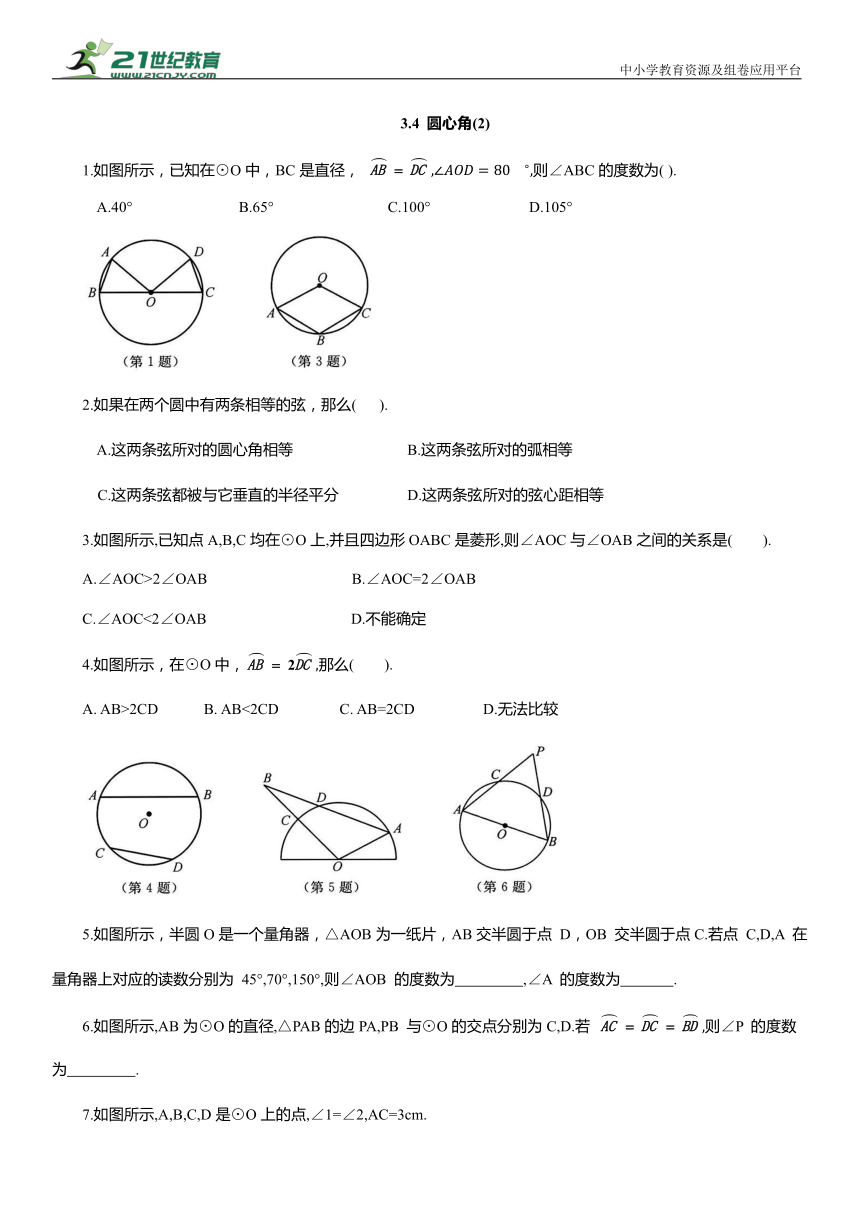 | |
| 格式 | docx | ||
| 文件大小 | 350.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-31 22:02:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
3.4 圆心角(2)
1.如图所示,已知在⊙O中,BC是直径, 则∠ABC的度数为( ).
A.40° B.65° C.100° D.105°
2.如果在两个圆中有两条相等的弦,那么( ).
A.这两条弦所对的圆心角相等 B.这两条弦所对的弧相等
C.这两条弦都被与它垂直的半径平分 D.这两条弦所对的弦心距相等
3.如图所示,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,则∠AOC与∠OAB之间的关系是( ).
A.∠AOC>2∠OAB B.∠AOC=2∠OAB
C.∠AOC<2∠OAB D.不能确定
4.如图所示,在⊙O中,那么( ).
A. AB>2CD B. AB<2CD C. AB=2CD D.无法比较
5.如图所示,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点 D,OB 交半圆于点C.若点 C,D,A 在量角器上对应的读数分别为 45°,70°,150°,则∠AOB 的度数为 ,∠A 的度数为 .
6.如图所示,AB为⊙O的直径,△PAB的边PA,PB 与⊙O的交点分别为C,D.若 则∠P 的度数为 .
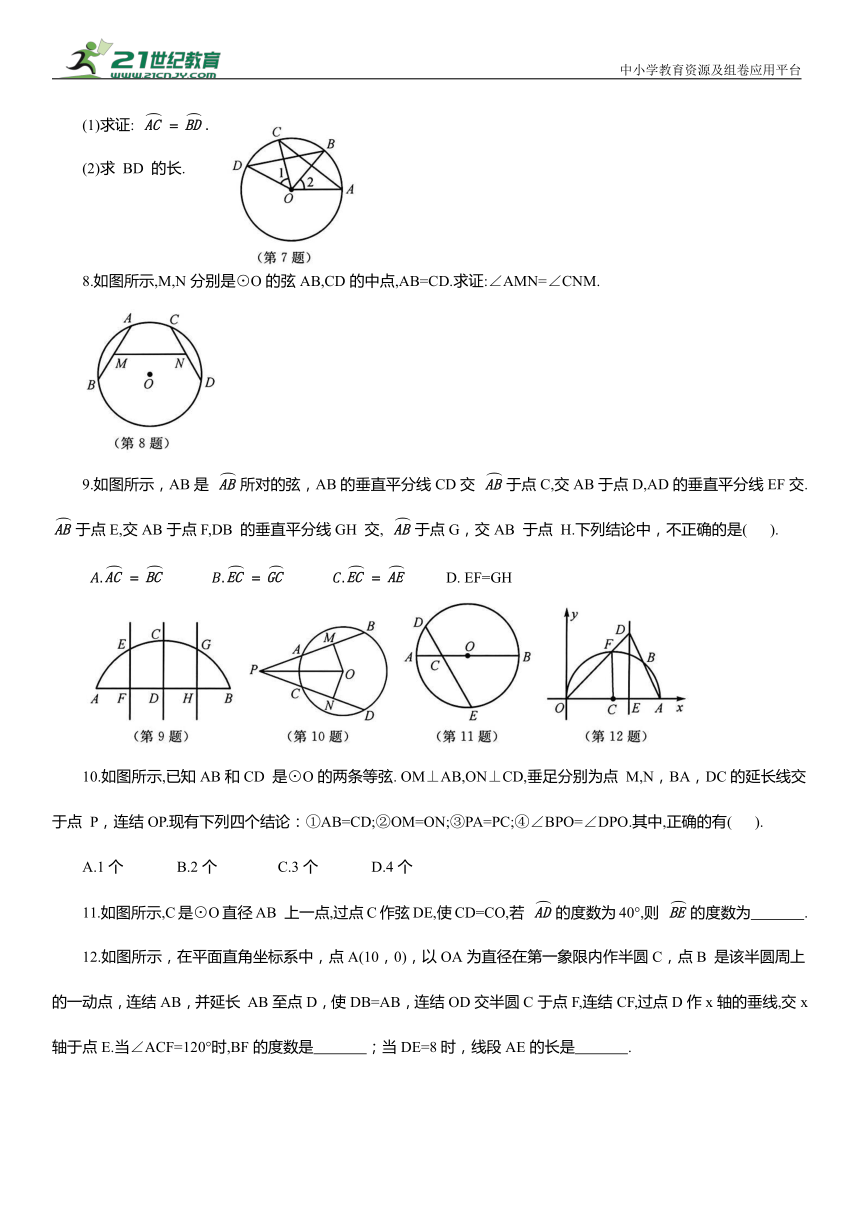
7.如图所示,A,B,C,D是⊙O上的点,∠1=∠2,AC=3cm.
(1)求证:
(2)求 BD 的长.
8.如图所示,M,N分别是⊙O的弦AB,CD的中点,AB=CD.求证:∠AMN=∠CNM.
9.如图所示,AB是 所对的弦,AB的垂直平分线CD交 于点C,交AB于点D,AD的垂直平分线EF交. 于点E,交AB于点F,DB 的垂直平分线GH 交, 于点G,交AB 于点 H.下列结论中,不正确的是( ).
D. EF=GH
10.如图所示,已知AB和CD 是⊙O的两条等弦. OM⊥AB,ON⊥CD,垂足分别为点 M,N,BA,DC的延长线交于点 P,连结OP.现有下列四个结论:①AB=CD;②OM=ON;③PA=PC;④∠BPO=∠DPO.其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
11.如图所示,C是⊙O直径AB 上一点,过点C作弦DE,使CD=CO,若 的度数为40°,则 的度数为 .
12.如图所示,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B 是该半圆周上的一动点,连结AB,并延长 AB至点D,使DB=AB,连结OD交半圆C于点F,连结CF,过点D作x轴的垂线,交x轴于点E.当∠ACF=120°时,BF的度数是 ;当DE=8时,线段AE的长是 .
13.如图所示,AB为⊙O的弦,半径OC,OD分别交AB 于点E,F,且
(1)求证:OE=OF.
(2)作半径ON⊥AB于点M,若AB=8,MN=2,求OM的长.
14.A,C是以半径为3的圆的圆周上的两点,B 为 的中点,以线段 BA,BC为邻边作菱形ABCD,顶点 D 恰好为该圆直径的三等分点,则该菱形的边长为( ).
A. 或2 B. 或2 C. 或 D. 或2
15.如图所示,AB是⊙O的直径,C 为 的中点,CF为⊙O的弦,且CF⊥AB,垂足为点 E,连结BD交CF 于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG.
(2)若AD=BE=2,求BF 的长.
16.已知AB是半径为1的⊙O的一条弦,且AB=a<1,以AB为一边在⊙O内作等边三角形ABC,D为⊙O上不同于点A 的一点,且DB=AB=a,DC的延长线交⊙O于点E.求AE 的长.
3.4 圆心角(2)
1. B 2. C 3. B 4. B 5.105° 50° 6.60°
7.(1)∵∠1=∠2,∴CD=AB.
(2)∵AC=BD,∴AC=BD.
∵AC=3cm,∴BD=3cm.
8.如答图所示,连结OM,ON.
∵点 O 为圆心,M,N 分别为弦AB,CD的中点,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.∴∠OMN=∠ONM.
∵∠AMN=90°-∠OMN,∠CNM=90°-∠ONM,
∴∠AMN=∠CNM.
9. C 10. D 11.120° 12.60° 4
13.(1)如答图1所示,连结OA,OB.
∵OA=OB,∴∠A=∠B.
∵AC=DB,∴∠AOE=∠BOF.
在△AOE 和△BOF中,
∴△AOE≌△BOF.∴OE=OF.
(2)如答图2所示,连结OA.∵OM⊥AB,∴AM= AB=4.设OM=x,则OA=ON=x+2.
在 Rt△AOM中,由勾股定理得 解得x=3.∴OM=3.
14. D 【解析】过点 B 作直径,连结AC交BO 于点 E.∵点 B为AC的中点,∴BD⊥AC.
如答图1所示,∵点 D恰在该圆直径的三等分点上,
∵四边形ABCD是菱形,
连结OC.在 Rt△OEC中, 在 Rt△DEC中,
如答图2所示, 同理可得OD=1,OE=1,DE=2.
连结OC,在 Rt△OEC中, 在 Rt△DEC中,
故选 D.
15.(1)∵C是BD的中点,
∵AB是⊙O的直径,且CF⊥AB,
在△BFG和△CDG中,7
∴△BFG≌△CDG.
(2)如答图所示,连结 OC 交 BD 于点 H.
∵C是BD 的中点,
∴OC⊥BD.∴DH=BH.
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH.∴OE=OH=1.∴OB=3.
16.如答图所示,连结OE,OA,OB.∵△ABC是等边三角形,∴AB=BC=AC=a,∠CAB=∠ACB=60°.
∴∠AED=∠AOB.
∵BC=AB=BD,
∴∠D=∠BCD.
∵∠EAB+∠D=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形.
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,AC=AB,∴△EAC≌△OAB.∴AE=OA=1.
3.4 圆心角(2)
1.如图所示,已知在⊙O中,BC是直径, 则∠ABC的度数为( ).
A.40° B.65° C.100° D.105°
2.如果在两个圆中有两条相等的弦,那么( ).
A.这两条弦所对的圆心角相等 B.这两条弦所对的弧相等
C.这两条弦都被与它垂直的半径平分 D.这两条弦所对的弦心距相等
3.如图所示,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,则∠AOC与∠OAB之间的关系是( ).
A.∠AOC>2∠OAB B.∠AOC=2∠OAB
C.∠AOC<2∠OAB D.不能确定
4.如图所示,在⊙O中,那么( ).
A. AB>2CD B. AB<2CD C. AB=2CD D.无法比较
5.如图所示,半圆O是一个量角器,△AOB为一纸片,AB交半圆于点 D,OB 交半圆于点C.若点 C,D,A 在量角器上对应的读数分别为 45°,70°,150°,则∠AOB 的度数为 ,∠A 的度数为 .
6.如图所示,AB为⊙O的直径,△PAB的边PA,PB 与⊙O的交点分别为C,D.若 则∠P 的度数为 .
7.如图所示,A,B,C,D是⊙O上的点,∠1=∠2,AC=3cm.
(1)求证:
(2)求 BD 的长.
8.如图所示,M,N分别是⊙O的弦AB,CD的中点,AB=CD.求证:∠AMN=∠CNM.
9.如图所示,AB是 所对的弦,AB的垂直平分线CD交 于点C,交AB于点D,AD的垂直平分线EF交. 于点E,交AB于点F,DB 的垂直平分线GH 交, 于点G,交AB 于点 H.下列结论中,不正确的是( ).
D. EF=GH
10.如图所示,已知AB和CD 是⊙O的两条等弦. OM⊥AB,ON⊥CD,垂足分别为点 M,N,BA,DC的延长线交于点 P,连结OP.现有下列四个结论:①AB=CD;②OM=ON;③PA=PC;④∠BPO=∠DPO.其中,正确的有( ).
A.1个 B.2个 C.3个 D.4个
11.如图所示,C是⊙O直径AB 上一点,过点C作弦DE,使CD=CO,若 的度数为40°,则 的度数为 .
12.如图所示,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆C,点B 是该半圆周上的一动点,连结AB,并延长 AB至点D,使DB=AB,连结OD交半圆C于点F,连结CF,过点D作x轴的垂线,交x轴于点E.当∠ACF=120°时,BF的度数是 ;当DE=8时,线段AE的长是 .
13.如图所示,AB为⊙O的弦,半径OC,OD分别交AB 于点E,F,且
(1)求证:OE=OF.
(2)作半径ON⊥AB于点M,若AB=8,MN=2,求OM的长.
14.A,C是以半径为3的圆的圆周上的两点,B 为 的中点,以线段 BA,BC为邻边作菱形ABCD,顶点 D 恰好为该圆直径的三等分点,则该菱形的边长为( ).
A. 或2 B. 或2 C. 或 D. 或2
15.如图所示,AB是⊙O的直径,C 为 的中点,CF为⊙O的弦,且CF⊥AB,垂足为点 E,连结BD交CF 于点G,连结CD,AD,BF.
(1)求证:△BFG≌△CDG.
(2)若AD=BE=2,求BF 的长.
16.已知AB是半径为1的⊙O的一条弦,且AB=a<1,以AB为一边在⊙O内作等边三角形ABC,D为⊙O上不同于点A 的一点,且DB=AB=a,DC的延长线交⊙O于点E.求AE 的长.
3.4 圆心角(2)
1. B 2. C 3. B 4. B 5.105° 50° 6.60°
7.(1)∵∠1=∠2,∴CD=AB.
(2)∵AC=BD,∴AC=BD.
∵AC=3cm,∴BD=3cm.
8.如答图所示,连结OM,ON.
∵点 O 为圆心,M,N 分别为弦AB,CD的中点,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.∴∠OMN=∠ONM.
∵∠AMN=90°-∠OMN,∠CNM=90°-∠ONM,
∴∠AMN=∠CNM.
9. C 10. D 11.120° 12.60° 4
13.(1)如答图1所示,连结OA,OB.
∵OA=OB,∴∠A=∠B.
∵AC=DB,∴∠AOE=∠BOF.
在△AOE 和△BOF中,
∴△AOE≌△BOF.∴OE=OF.
(2)如答图2所示,连结OA.∵OM⊥AB,∴AM= AB=4.设OM=x,则OA=ON=x+2.
在 Rt△AOM中,由勾股定理得 解得x=3.∴OM=3.
14. D 【解析】过点 B 作直径,连结AC交BO 于点 E.∵点 B为AC的中点,∴BD⊥AC.
如答图1所示,∵点 D恰在该圆直径的三等分点上,
∵四边形ABCD是菱形,
连结OC.在 Rt△OEC中, 在 Rt△DEC中,
如答图2所示, 同理可得OD=1,OE=1,DE=2.
连结OC,在 Rt△OEC中, 在 Rt△DEC中,
故选 D.
15.(1)∵C是BD的中点,
∵AB是⊙O的直径,且CF⊥AB,
在△BFG和△CDG中,7
∴△BFG≌△CDG.
(2)如答图所示,连结 OC 交 BD 于点 H.
∵C是BD 的中点,
∴OC⊥BD.∴DH=BH.
∵OC=OB,∠COE=∠BOH,∠OHB=∠OEC=90°,
∴△COE≌△BOH.∴OE=OH=1.∴OB=3.
16.如答图所示,连结OE,OA,OB.∵△ABC是等边三角形,∴AB=BC=AC=a,∠CAB=∠ACB=60°.
∴∠AED=∠AOB.
∵BC=AB=BD,
∴∠D=∠BCD.
∵∠EAB+∠D=180°,
∴∠ECA=∠EAC,即△EAC是等腰三角形.
在等腰△EAC和等腰△OAB中,∠AEC=∠AOB,AC=AB,∴△EAC≌△OAB.∴AE=OA=1.
同课章节目录
