4.5相似三角形的性质及其应用(1)提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.5相似三角形的性质及其应用(1)提优训练(含答案)2024-2025学年浙教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 337.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 00:00:00 | ||
图片预览



文档简介
4.5 相似三角形的性质及其应用(1)
基础巩固
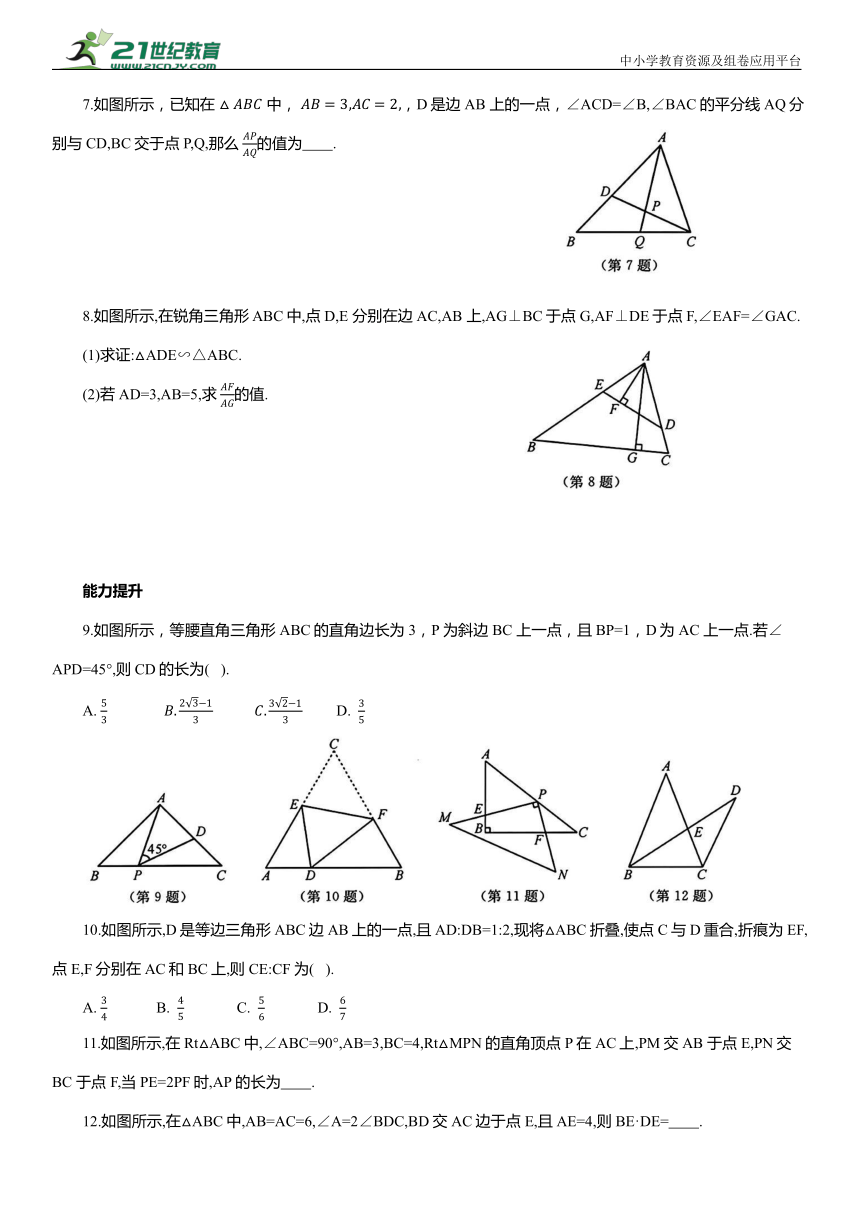
1.如图所示,在 ABCD中,E是边BC上的点,AE交BD 于点F,若BE:BC=2:3,则下列选项中,错误的是( ).
2.如图所示,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点 F 为BC 边上一点,连结AF交DE 于点G,则下列结论中,正确的是( ).
3.如图所示,AB是⊙O的直径,过点O作AB 的垂线与弦AC交于点D,连结 BC,若OD=3,⊙O的半径为4,则CD的长为( ).
A.1.4 B.1.8 C.2.4 D.2.6
4.如图所示,边长为12的正方形ABCD中,有一个小正方形EFGH,其中点 E,F,G分别在AB,BC,FD上.若BF=3,则小正方形的边长为( ).
A.1 C.4 D.5
5.如图所示,点D,E分别在AB,AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为 .
中小学教育资源及组卷应用平台
6.如图所示,在 ABCD中,E是边BC上的点,AE交BD 于点F,如果 那么 的值为 .
7.如图所示,已知在 中, ,D是边AB 上的一点,∠ACD=∠B,∠BAC的平分线AQ分别与CD,BC交于点P,Q,那么 的值为 .
8.如图所示,在锐角三角形 ABC中,点 D,E 分别在边AC,AB 上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC.
(2)若AD=3,AB=5,求 的值.
能力提升
9.如图所示,等腰直角三角形ABC的直角边长为3,P 为斜边 BC 上一点,且BP=1,D为AC 上一点.若∠APD=45°,则CD的长为( ).
A. D.
10.如图所示,D是等边三角形ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点 E,F分别在AC和BC上,则CE:CF为( ).
A. B. C. D.
11.如图所示,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN的直角顶点 P 在AC上,PM交AB 于点E,PN交BC 于点F,当PE=2PF时,AP 的长为 .
12.如图所示,在△ABC中,AB=AC=6,∠A=2∠BDC,BD交AC边于点E,且AE=4,则BE·DE= .
13.如图所示,在四边形ABCD中, ,对角线 AC,BD交于点E,且
(1)求证:
(2)F是BC 边上一点,连结 AF 与BD 交于点G,如果 求证:
14.如图所示,在平面直角坐标系中,直线y=-x+3与x轴交于点C,与直线AD交于点 点D的坐标为(0,1).
(1)求直线AD的函数表达式.
(2)直线AD与x轴交于点B,若E是直线AD 上一动点(不与点 B 重合),当 与△BCE 相似时,求点 E 的坐标.
实战演练
15.如图所示,在 ABCD中,∠ABC 的平分线交AC 于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则 的值为( ).
16.如图所示,在矩形 ABCD 中, ,AF 平分 分别交 DC,BC的延长线于点E,F,连结 DF,过点 A 作. 分别交 BD,BF于点G,H.
(1)求 DE的长.
(2)求证:∠1=∠DFC.
应用探究
17.秀秀同学遇到了这样一个问题:如图1所示,已知AF,BE 是△ABC的中线,且. BE,垂足为点 P,设BC=a,AC=b,AB=c.求证:
该同学仔细分析后,得到如下解题思路:先连结 EF,利用EF 为△ABC的中位线得到 故 设 用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF 中利用勾股定理计算,消去m,n即可得证.
(1)请你根据以上解题思路帮秀秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连结BE,CF 并延长交于点M,BM,CM分别交AD 于点G,H,如图2所示,求 的值.
4.5 相似三角形的性质及其应用(1)
1. C 2. C 3. A 4. A 5.10 6. 7.
8.(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,∴∠AED=∠ACB.
又∵∠EAD=∠BAC,∴△ADE∽△ABC.
(2)由(1)知△ADE∽△ABC,∴AB=AE=
∵∠AFE=∠AGC,∠EAF=∠CAG,
9. C 10. B 11.3
12.20 【解析】如答图所示,延长 CA到点 F,使得 AF=AB,连结 BF,则
∵∠BAC=2∠BDC,
∴∠F=∠BDC.
又∵∠FEB=∠DEC,∴△FEB∽
∵AE=4,AB=AC=6,∴EF=10,CE=2.
13.(1)∵AD∥BC,∠BCD=90°,∴∠ADC=∠BCD=90°.
∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90°.
∴∠ACD=∠CBD.∴△ACD∽△DBC.
即CD =BC·AD.
(2)∵AD∥BC,∴∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.
∵∠ABG=∠DBA,∴△ABG∽△DBA.∴AB=ABD.
14.(1)设直线 AD的函数表达式为 y= kx+b.
将 D(0,1)代入,
得 解得
∴直线 AD的函数表达式为
(2)∵直线AD与x轴的交点为(-2,0),∴OB=2.
∵点 D的坐标为(0,1),∴OD=1.
∵y=-x+3与x轴交于点C(3,0),
①如答图1所示,当∵△BOD∽△BCE时,
则
解得
∴点 E的坐标为(3, ).
②如答图2所示,当△BOD∽△BEC时,则
解得
过点 E作 EF⊥x轴于点 F,易知△BEF∽△BCE,
即 解得 EF=2.
∴点 E的坐标为(2,2).
综上可得点E的坐标为(3, )或(2,2).
15. C 【解析】由 AF=2DF,可以假设 DF=k,则 AF=2k,AD=3k.
∵四边形 ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD.
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G.
∵BE平分∠ABC,∴∠ABF=∠CBG.
∴∠ABF=∠AFB=∠DFG=∠G.
∴AB=CD=2k,DF=DG=k.∴CG=CD+DG=3k.
∵AB∥DG,∴△ABE∽△CGE.
故选 C.
16.(1)∵矩形ABCD中,AD∥CF,∴∠DAF=∠AFC.
∵AF平分∠DAC,∴∠DAF=∠CAF.
∴∠FAC=∠AFC.∴AC=CF.
∴CF=5.
∵AD∥CF,∴△ADE∽△FCE.∴△F=DE.
设DE=x,则 解得
(2)∵AD∥FH,AH∥DF,
∴四边形 ADFH 是平行四边形.
∴AD=FH=3.∴CH=2,BH=5.
∵AD∥BH,∴△ADG∽△HBG.
∴EG∥BC.∴∠1=∠AHC.
又∵DF∥AH,∴∠AHC=∠DFC.∴∠1=∠DFC.
17.(1)设 PF=m,PE=n,连结 EF.
∵AF,BE是△ABC的中线,
∴EF为△ABC的中位线,
∴EF∥AB,EF= c.∴△EPF∽△BPA.
即
∴PB=2n,PA=2m.
在 Rt△AEP中,
在 Rt△BFP 中,
①+②得
在 Rt△EFP 中,'
(2)∵四边形 ABCD为菱形,∴BD⊥AC.
∵E,F分别为线段AO,DO的中点,
由(1)的结论得.
∵AG∥BC,∴△AEG∽△CEB.
.
同理可得DH=1,∴GH=1.
∴MB=3MG,MC=3MH.
基础巩固
1.如图所示,在 ABCD中,E是边BC上的点,AE交BD 于点F,若BE:BC=2:3,则下列选项中,错误的是( ).
2.如图所示,在△ABC中,D,E分别为AB,AC边上的点,DE∥BC,点 F 为BC 边上一点,连结AF交DE 于点G,则下列结论中,正确的是( ).
3.如图所示,AB是⊙O的直径,过点O作AB 的垂线与弦AC交于点D,连结 BC,若OD=3,⊙O的半径为4,则CD的长为( ).
A.1.4 B.1.8 C.2.4 D.2.6
4.如图所示,边长为12的正方形ABCD中,有一个小正方形EFGH,其中点 E,F,G分别在AB,BC,FD上.若BF=3,则小正方形的边长为( ).
A.1 C.4 D.5
5.如图所示,点D,E分别在AB,AC上,且∠ABC=∠AED,若DE=4,AE=5,BC=8,则AB的长为 .
中小学教育资源及组卷应用平台
6.如图所示,在 ABCD中,E是边BC上的点,AE交BD 于点F,如果 那么 的值为 .
7.如图所示,已知在 中, ,D是边AB 上的一点,∠ACD=∠B,∠BAC的平分线AQ分别与CD,BC交于点P,Q,那么 的值为 .
8.如图所示,在锐角三角形 ABC中,点 D,E 分别在边AC,AB 上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC.
(2)若AD=3,AB=5,求 的值.
能力提升
9.如图所示,等腰直角三角形ABC的直角边长为3,P 为斜边 BC 上一点,且BP=1,D为AC 上一点.若∠APD=45°,则CD的长为( ).
A. D.
10.如图所示,D是等边三角形ABC边AB上的一点,且AD:DB=1:2,现将△ABC折叠,使点C与D重合,折痕为EF,点 E,F分别在AC和BC上,则CE:CF为( ).
A. B. C. D.
11.如图所示,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN的直角顶点 P 在AC上,PM交AB 于点E,PN交BC 于点F,当PE=2PF时,AP 的长为 .
12.如图所示,在△ABC中,AB=AC=6,∠A=2∠BDC,BD交AC边于点E,且AE=4,则BE·DE= .
13.如图所示,在四边形ABCD中, ,对角线 AC,BD交于点E,且
(1)求证:
(2)F是BC 边上一点,连结 AF 与BD 交于点G,如果 求证:
14.如图所示,在平面直角坐标系中,直线y=-x+3与x轴交于点C,与直线AD交于点 点D的坐标为(0,1).
(1)求直线AD的函数表达式.
(2)直线AD与x轴交于点B,若E是直线AD 上一动点(不与点 B 重合),当 与△BCE 相似时,求点 E 的坐标.
实战演练
15.如图所示,在 ABCD中,∠ABC 的平分线交AC 于点E,交AD于点F,交CD的延长线于点G.若AF=2FD,则 的值为( ).
16.如图所示,在矩形 ABCD 中, ,AF 平分 分别交 DC,BC的延长线于点E,F,连结 DF,过点 A 作. 分别交 BD,BF于点G,H.
(1)求 DE的长.
(2)求证:∠1=∠DFC.
应用探究
17.秀秀同学遇到了这样一个问题:如图1所示,已知AF,BE 是△ABC的中线,且. BE,垂足为点 P,设BC=a,AC=b,AB=c.求证:
该同学仔细分析后,得到如下解题思路:先连结 EF,利用EF 为△ABC的中位线得到 故 设 用m,n把PA,PB分别表示出来,再在Rt△APE,Rt△BPF 中利用勾股定理计算,消去m,n即可得证.
(1)请你根据以上解题思路帮秀秀同学写出证明过程.
(2)利用题中的结论,解答下列问题:
在边长为3的菱形ABCD中,O为对角线AC,BD的交点,E,F分别为线段AO,DO的中点,连结BE,CF 并延长交于点M,BM,CM分别交AD 于点G,H,如图2所示,求 的值.
4.5 相似三角形的性质及其应用(1)
1. C 2. C 3. A 4. A 5.10 6. 7.
8.(1)∵AG⊥BC,AF⊥DE,∴∠AFE=∠AGC=90°.
∵∠EAF=∠GAC,∴∠AED=∠ACB.
又∵∠EAD=∠BAC,∴△ADE∽△ABC.
(2)由(1)知△ADE∽△ABC,∴AB=AE=
∵∠AFE=∠AGC,∠EAF=∠CAG,
9. C 10. B 11.3
12.20 【解析】如答图所示,延长 CA到点 F,使得 AF=AB,连结 BF,则
∵∠BAC=2∠BDC,
∴∠F=∠BDC.
又∵∠FEB=∠DEC,∴△FEB∽
∵AE=4,AB=AC=6,∴EF=10,CE=2.
13.(1)∵AD∥BC,∠BCD=90°,∴∠ADC=∠BCD=90°.
∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90°.
∴∠ACD=∠CBD.∴△ACD∽△DBC.
即CD =BC·AD.
(2)∵AD∥BC,∴∠ADB=∠DBF.
∵∠BAF=∠DBF,∴∠ADB=∠BAF.
∵∠ABG=∠DBA,∴△ABG∽△DBA.∴AB=ABD.
14.(1)设直线 AD的函数表达式为 y= kx+b.
将 D(0,1)代入,
得 解得
∴直线 AD的函数表达式为
(2)∵直线AD与x轴的交点为(-2,0),∴OB=2.
∵点 D的坐标为(0,1),∴OD=1.
∵y=-x+3与x轴交于点C(3,0),
①如答图1所示,当∵△BOD∽△BCE时,
则
解得
∴点 E的坐标为(3, ).
②如答图2所示,当△BOD∽△BEC时,则
解得
过点 E作 EF⊥x轴于点 F,易知△BEF∽△BCE,
即 解得 EF=2.
∴点 E的坐标为(2,2).
综上可得点E的坐标为(3, )或(2,2).
15. C 【解析】由 AF=2DF,可以假设 DF=k,则 AF=2k,AD=3k.
∵四边形 ABCD是平行四边形,
∴AD∥BC,AB∥CD,AB=CD.
∴∠AFB=∠FBC=∠DFG,∠ABF=∠G.
∵BE平分∠ABC,∴∠ABF=∠CBG.
∴∠ABF=∠AFB=∠DFG=∠G.
∴AB=CD=2k,DF=DG=k.∴CG=CD+DG=3k.
∵AB∥DG,∴△ABE∽△CGE.
故选 C.
16.(1)∵矩形ABCD中,AD∥CF,∴∠DAF=∠AFC.
∵AF平分∠DAC,∴∠DAF=∠CAF.
∴∠FAC=∠AFC.∴AC=CF.
∴CF=5.
∵AD∥CF,∴△ADE∽△FCE.∴△F=DE.
设DE=x,则 解得
(2)∵AD∥FH,AH∥DF,
∴四边形 ADFH 是平行四边形.
∴AD=FH=3.∴CH=2,BH=5.
∵AD∥BH,∴△ADG∽△HBG.
∴EG∥BC.∴∠1=∠AHC.
又∵DF∥AH,∴∠AHC=∠DFC.∴∠1=∠DFC.
17.(1)设 PF=m,PE=n,连结 EF.
∵AF,BE是△ABC的中线,
∴EF为△ABC的中位线,
∴EF∥AB,EF= c.∴△EPF∽△BPA.
即
∴PB=2n,PA=2m.
在 Rt△AEP中,
在 Rt△BFP 中,
①+②得
在 Rt△EFP 中,'
(2)∵四边形 ABCD为菱形,∴BD⊥AC.
∵E,F分别为线段AO,DO的中点,
由(1)的结论得.
∵AG∥BC,∴△AEG∽△CEB.
.
同理可得DH=1,∴GH=1.
∴MB=3MG,MC=3MH.
同课章节目录
