第4章 相似三角形单元测试卷(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 第4章 相似三角形单元测试卷(含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 416.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:24:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第4章 相似三角形单元测试卷
1.若x:y=2:3,则下列各式中,不成立的是( ).
2.下列图形中,一定相似的一组是( ).
A.邻边对应成比例的两个平行四边形 B.有一个内角相等的两个菱形
C.腰长对应成比例的两个等腰三角形 D.有一条边相等的两个矩形
3.如图所示,E为 ABCD的边AD上的一点,且AE:ED=3:2,CE交BD 于点F,则BF: FD为( ).
A.3:5 B.5:3 C.2:5 D.5:2
4.网球单打比赛场地的宽为8m,长在球网的两侧各有12m,球网的高为0.9m(即图中AB的高度).网球比赛中,某运动员退出场地在距球网14m的D点处接球,设计打出直线穿越球,使球落在对方底线上的点C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点的高度至少要为( ).
A.1.65m B.1.75m C.1.85m D.1.95m
5.如图所示,△PQR 在由边长为1个单位的小正方形组成的方格纸中,它的顶点在小正方形顶点的位置,其中点 A,B,C,D也是小正方形的顶点,那么与△PQR 相似的是( ).
A.以点 P,Q,A为顶点的三角形 B.以点 P,Q,B为顶点的三角形
C.以点 P,Q,C为顶点的三角形 D.以点 P,Q,D为顶点的三角形
6.如图所示,在正方形ABCD中,E是BC的中点,△DEF的面积为2,则正方形 ABCD的面积为( ).
A.6 B.12 C.16 D.20
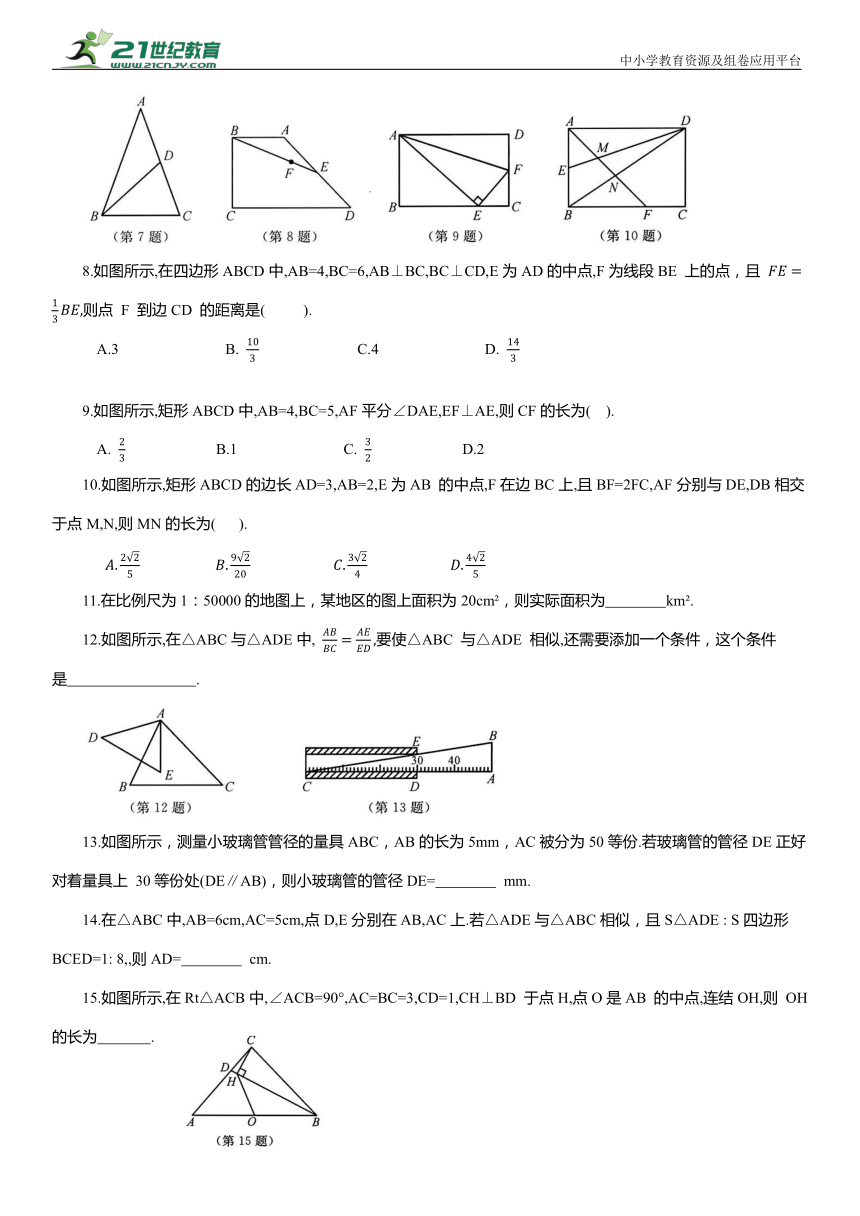
7.如图所示,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC.下列结论中,正确的是( ).
A. AD=2
8.如图所示,在四边形ABCD中,AB=4,BC=6,AB⊥BC,BC⊥CD,E为AD的中点,F为线段BE 上的点,且 则点 F 到边CD 的距离是( ).
A.3 B. C.4 D.
9.如图所示,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF的长为( ).
A. B.1 C. D.2
10.如图所示,矩形ABCD的边长AD=3,AB=2,E为AB 的中点,F在边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N,则MN的长为( ).
11.在比例尺为1:50000的地图上,某地区的图上面积为20cm ,则实际面积为 km .
12.如图所示,在△ABC与△ADE中, 要使△ABC 与△ADE 相似,还需要添加一个条件,这个条件是 .
13.如图所示,测量小玻璃管管径的量具ABC,AB的长为5mm,AC被分为50等份.若玻璃管的管径DE正好对着量具上 30等份处(DE∥AB),则小玻璃管的管径DE= mm.
14.在△ABC中,AB=6cm,AC=5cm,点D,E分别在AB,AC上.若△ADE与△ABC相似,且S△ADE : S四边形BCED=1: 8,,则AD= cm.
15.如图所示,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD 于点H,点O是AB 的中点,连结OH,则 OH 的长为 .
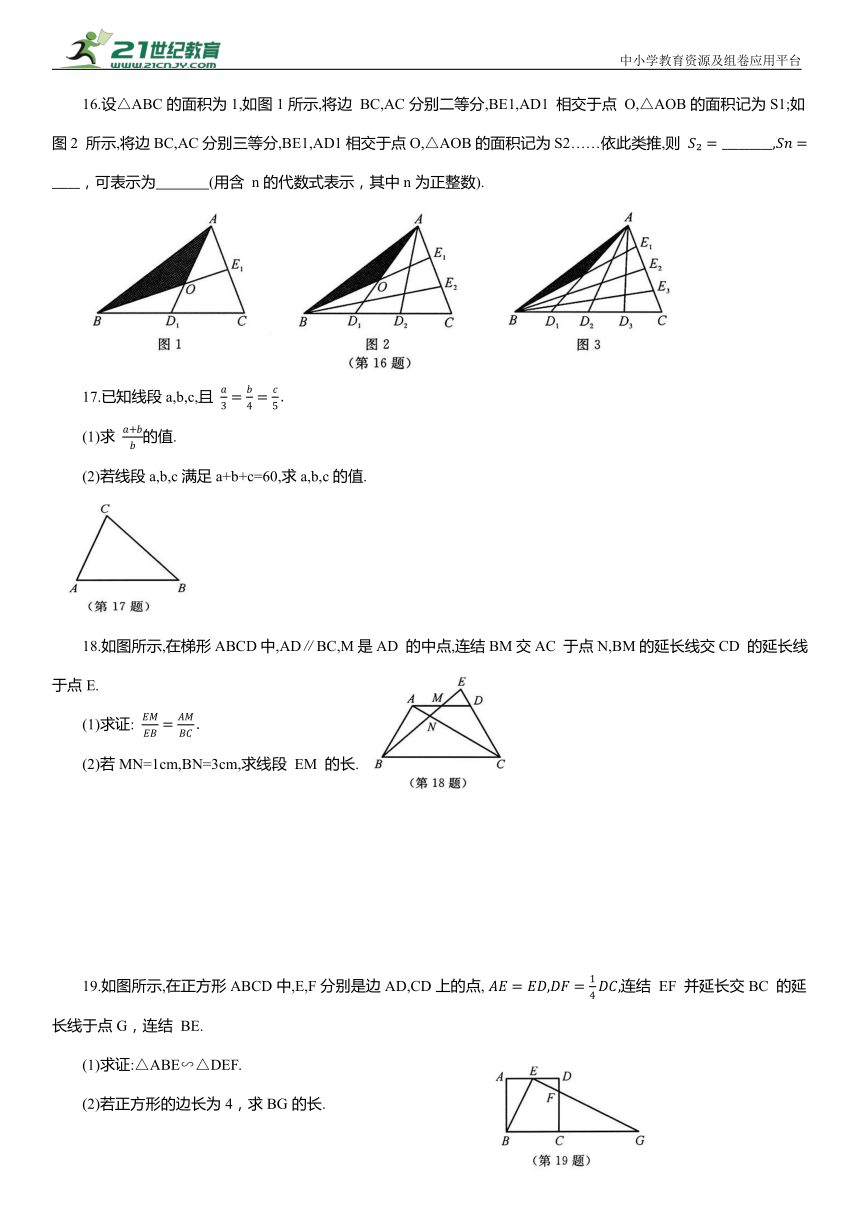
16.设△ABC的面积为1,如图1所示,将边 BC,AC分别二等分,BE1,AD1 相交于点 O,△AOB的面积记为S1;如图2 所示,将边BC,AC分别三等分,BE1,AD1相交于点O,△AOB的面积记为S2……依此类推,则 ,可表示为 (用含 n的代数式表示,其中n为正整数).
17.已知线段a,b,c,且
(1)求 的值.
(2)若线段a,b,c满足a+b+c=60,求a,b,c的值.
18.如图所示,在梯形ABCD中,AD∥BC,M是AD 的中点,连结BM交AC 于点N,BM的延长线交CD 的延长线于点E.
(1)求证:
(2)若MN=1cm,BN=3cm,求线段 EM 的长.
19.如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点, 连结 EF 并延长交BC 的延长线于点G,连结 BE.
(1)求证:△ABE∽△DEF.
(2)若正方形的边长为4,求BG的长.
20.如图所示,为测量学校围墙外直立电线杆AB 的高度,小亮在操场上点C处直立一根高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B 重合;小亮又在点 C1 处直立一根高3m的竹竿 然后退到点 E1 处,此时恰好看到竹竿顶端D1 与电线杆顶端B重合.小亮的眼睛离地面的高度 量得
(1)△FDM∽ ,△F1D1N∽ .
(2)求电线杆AB的高度.
21.如图所示,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连结DE 和DB,过点 E作EF⊥AB,垂足为点 F,交 BD于点 P.
(1)求证:AD=DE.
(2)若CE=2,求线段CD 的长.
(3)在(2)的条件下,求△DPE 的面积.
22.如图所示,在矩形ABCD中,AD=4,AB=m(m>4),P是AB 边上的任意一点(不与点A,B重合),连结 PD,过点 P作PQ⊥PD交直线BC 于点Q.
(1)当m=10时,是否存在点 P 使得点Q 与点C 重合 若存在,求出此时AP 的长;若不存在,说明理由.
(2)连结AC,若PQ∥AC,求线段BQ的长(用含 m的代数式表示).
(3)若△PQD为等腰三角形,求以点P,Q,C,D为顶点的四边形的面积S关于m 的函数表达式,并写出m的取值范围.
23.如图1所示,在△ABC中,O是AC上一点,过点O的直线与AB 及BC 的延长线分别相交于点 M,N.
(1)若点O是AC 的中点, 求 的值.
(温馨提示:过点 A 作MN 的平行线交 BN 的延长线于点G.)
(2)若O是AC上任意一点(不与点A,C重合),求证:
(3)如图2所示,P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F,若 求 的值.
1. D 2. B 3. D 4. D 5. B 6. B 7. C 8. C 9. C10. B 11.5 12.∠B=∠E 13.3 14.2或
【解析】如答图所示,在 BD上截取 BE=CH,连结CO,OE.
在 Rt△BCD中,CD=1,BC=3,∴BD=
∵∠ACB=90°,CH⊥BD,
易证△CDH∽△BDC.
即 解得
∵△ACB是等腰直角三角形,O是AB 中点,
∴AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°.
∴∠OCH+∠DCH=45°,∠ABD+∠DBC=45°.
∵∠DCH=∠CBD,∴∠OCH=∠ABD.
在△CHO与△BEO中,.
∴△CHO≌△BEO.∴OE=OH,∠BOE=∠HOC.
∵OC⊥BO,∴∠EOH=90°,即△HOE是等腰直角三角形.
17.设 则a=3k,b=4k,c=5k.
(2)∵a+b+c=60,∴3k+4k+5k=60,解得k=5.
∴a=3k=15,b=4k=20,c=5k=25.
18.(1)∵AD∥BC,∴△MED∽△BEC.∴BB=MDC.
∵M是AD 的中点,.
∵EB=ME+MB,MB=BN+NM=4(cm),
19.(1)∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°.
∴AB=DE.∴△ABE∽△DEF.
(2)∵四边形ABCD为正方形,
正方形的边长为4,∴ED=2,CG=6.
∴BG=BC+CG=10.
20.(1)△FBG △F BG
即
∴GM=16(m).
∴BG=13.5(m).∴AB=BG+GA=15(m).
∴电线杆 AB 的高度为15m.
21.(1)∵AB是⊙O的直径,∴∠ADB=90°.
∵AB=BC,∴D是AC 的中点,∠ABD=∠CBD.
∴AD=DE.
(2)∵四边形 ABED内接于⊙O,∴∠CED=∠CAB.
∵∠C=∠C,∴△CED∽△CAB.∴CA=CD.
∵AB=BC=10,CE=2,D是AC 的中点,.
(3)如答图所示,延长 EF 交⊙O于点M.BE=BC-CE=10-2=8,在 Rt△ABD中,
∵EM⊥AB,AB是⊙O的直径,
∴∠BEP=∠EDB.∴△BPE∽△BED.
,
22.(1)存在点 P.假设存在一点 P,使点 Q与点C 重合,如答图1所示,设AP 的长为x,则 BP=10-x.
在Rt△APD中,
在 Rt△PBC中,
在Rt△PCD 中, 即 (10-x) ,解得x=2或8.
故当m=10时,存在点 P 使得点 Q 与点C 重合,此时AP=2或8.
(2)连结AC,设BP=y,则AP=m-y.
∵PQ∥AC,∴△PBQ∽△ABC.
即
∵DP⊥PQ,∴∠APD+∠BPQ=90°.
∵∠BPQ+∠BQP=90°,
∴∠APD=∠BQP.∴△APD∽△BQP.
即
(3)①当点 Q在BC 上时,如答图3所示,连结 DQ.
∵PQ⊥PD,∴只有当 DP=PQ时,△PQD 为等腰三角形.
∵△APD∽△BQP,∴△BQP≌△APD.
∴PB=DA=4,AP=BQ=m-4.
∴以点 P,Q,C,D为顶点的四边形的面积S=S矩形ABCD一 =16(m≤8).
②当点 Q在BC 延长线上时,如答图4 所示,连结 DQ,PC.
∵DP=PQ,∴△DAP≌△PBQ.∴PB=AD=4,AB=BQ=m-4.
23.(1)如答图所示,过点 A 作AG∥MN 交 BN 延长线于点G.
∴∠G=∠BNM.又∵∠B=∠B,∴△ABG∽△MBN.
即
同理,在△ACG和△OCN 中,
∵O为AC 中点,∴AO=CO.∴NG=CN.
(2)由(1)知
(3)在△ABD 中,P 是AD 上的一点,过点 P 的直线与AB 及BD 的延长线分别相交于点 F,C,
由(2)得
在△ACD中,P 是AD 上一点,过点 P 的直线与AC 及CD 的延长线分别相交于点E,B,
由(2)得
第4章 相似三角形单元测试卷
1.若x:y=2:3,则下列各式中,不成立的是( ).
2.下列图形中,一定相似的一组是( ).
A.邻边对应成比例的两个平行四边形 B.有一个内角相等的两个菱形
C.腰长对应成比例的两个等腰三角形 D.有一条边相等的两个矩形
3.如图所示,E为 ABCD的边AD上的一点,且AE:ED=3:2,CE交BD 于点F,则BF: FD为( ).
A.3:5 B.5:3 C.2:5 D.5:2
4.网球单打比赛场地的宽为8m,长在球网的两侧各有12m,球网的高为0.9m(即图中AB的高度).网球比赛中,某运动员退出场地在距球网14m的D点处接球,设计打出直线穿越球,使球落在对方底线上的点C处,用刁钻的落点牵制对方.在这次进攻过程中,为保证战术成功,该运动员击球点的高度至少要为( ).
A.1.65m B.1.75m C.1.85m D.1.95m
5.如图所示,△PQR 在由边长为1个单位的小正方形组成的方格纸中,它的顶点在小正方形顶点的位置,其中点 A,B,C,D也是小正方形的顶点,那么与△PQR 相似的是( ).
A.以点 P,Q,A为顶点的三角形 B.以点 P,Q,B为顶点的三角形
C.以点 P,Q,C为顶点的三角形 D.以点 P,Q,D为顶点的三角形
6.如图所示,在正方形ABCD中,E是BC的中点,△DEF的面积为2,则正方形 ABCD的面积为( ).
A.6 B.12 C.16 D.20
7.如图所示,在△ABC中,AB=AC=3,BC=2,点D在腰AC上,且BD=BC.下列结论中,正确的是( ).
A. AD=2
8.如图所示,在四边形ABCD中,AB=4,BC=6,AB⊥BC,BC⊥CD,E为AD的中点,F为线段BE 上的点,且 则点 F 到边CD 的距离是( ).
A.3 B. C.4 D.
9.如图所示,矩形ABCD中,AB=4,BC=5,AF平分∠DAE,EF⊥AE,则CF的长为( ).
A. B.1 C. D.2
10.如图所示,矩形ABCD的边长AD=3,AB=2,E为AB 的中点,F在边BC上,且BF=2FC,AF分别与DE,DB相交于点M,N,则MN的长为( ).
11.在比例尺为1:50000的地图上,某地区的图上面积为20cm ,则实际面积为 km .
12.如图所示,在△ABC与△ADE中, 要使△ABC 与△ADE 相似,还需要添加一个条件,这个条件是 .
13.如图所示,测量小玻璃管管径的量具ABC,AB的长为5mm,AC被分为50等份.若玻璃管的管径DE正好对着量具上 30等份处(DE∥AB),则小玻璃管的管径DE= mm.
14.在△ABC中,AB=6cm,AC=5cm,点D,E分别在AB,AC上.若△ADE与△ABC相似,且S△ADE : S四边形BCED=1: 8,,则AD= cm.
15.如图所示,在Rt△ACB中,∠ACB=90°,AC=BC=3,CD=1,CH⊥BD 于点H,点O是AB 的中点,连结OH,则 OH 的长为 .
16.设△ABC的面积为1,如图1所示,将边 BC,AC分别二等分,BE1,AD1 相交于点 O,△AOB的面积记为S1;如图2 所示,将边BC,AC分别三等分,BE1,AD1相交于点O,△AOB的面积记为S2……依此类推,则 ,可表示为 (用含 n的代数式表示,其中n为正整数).
17.已知线段a,b,c,且
(1)求 的值.
(2)若线段a,b,c满足a+b+c=60,求a,b,c的值.
18.如图所示,在梯形ABCD中,AD∥BC,M是AD 的中点,连结BM交AC 于点N,BM的延长线交CD 的延长线于点E.
(1)求证:
(2)若MN=1cm,BN=3cm,求线段 EM 的长.
19.如图所示,在正方形ABCD中,E,F分别是边AD,CD上的点, 连结 EF 并延长交BC 的延长线于点G,连结 BE.
(1)求证:△ABE∽△DEF.
(2)若正方形的边长为4,求BG的长.
20.如图所示,为测量学校围墙外直立电线杆AB 的高度,小亮在操场上点C处直立一根高3m的竹竿CD,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B 重合;小亮又在点 C1 处直立一根高3m的竹竿 然后退到点 E1 处,此时恰好看到竹竿顶端D1 与电线杆顶端B重合.小亮的眼睛离地面的高度 量得
(1)△FDM∽ ,△F1D1N∽ .
(2)求电线杆AB的高度.
21.如图所示,在△ABC中,AB=BC=10,以AB为直径作⊙O分别交AC,BC于点D,E,连结DE 和DB,过点 E作EF⊥AB,垂足为点 F,交 BD于点 P.
(1)求证:AD=DE.
(2)若CE=2,求线段CD 的长.
(3)在(2)的条件下,求△DPE 的面积.
22.如图所示,在矩形ABCD中,AD=4,AB=m(m>4),P是AB 边上的任意一点(不与点A,B重合),连结 PD,过点 P作PQ⊥PD交直线BC 于点Q.
(1)当m=10时,是否存在点 P 使得点Q 与点C 重合 若存在,求出此时AP 的长;若不存在,说明理由.
(2)连结AC,若PQ∥AC,求线段BQ的长(用含 m的代数式表示).
(3)若△PQD为等腰三角形,求以点P,Q,C,D为顶点的四边形的面积S关于m 的函数表达式,并写出m的取值范围.
23.如图1所示,在△ABC中,O是AC上一点,过点O的直线与AB 及BC 的延长线分别相交于点 M,N.
(1)若点O是AC 的中点, 求 的值.
(温馨提示:过点 A 作MN 的平行线交 BN 的延长线于点G.)
(2)若O是AC上任意一点(不与点A,C重合),求证:
(3)如图2所示,P是△ABC内任意一点,射线AP,BP,CP分别交BC,AC,AB于点D,E,F,若 求 的值.
1. D 2. B 3. D 4. D 5. B 6. B 7. C 8. C 9. C10. B 11.5 12.∠B=∠E 13.3 14.2或
【解析】如答图所示,在 BD上截取 BE=CH,连结CO,OE.
在 Rt△BCD中,CD=1,BC=3,∴BD=
∵∠ACB=90°,CH⊥BD,
易证△CDH∽△BDC.
即 解得
∵△ACB是等腰直角三角形,O是AB 中点,
∴AO=OB=OC,∠A=∠ACO=∠BCO=∠ABC=45°.
∴∠OCH+∠DCH=45°,∠ABD+∠DBC=45°.
∵∠DCH=∠CBD,∴∠OCH=∠ABD.
在△CHO与△BEO中,.
∴△CHO≌△BEO.∴OE=OH,∠BOE=∠HOC.
∵OC⊥BO,∴∠EOH=90°,即△HOE是等腰直角三角形.
17.设 则a=3k,b=4k,c=5k.
(2)∵a+b+c=60,∴3k+4k+5k=60,解得k=5.
∴a=3k=15,b=4k=20,c=5k=25.
18.(1)∵AD∥BC,∴△MED∽△BEC.∴BB=MDC.
∵M是AD 的中点,.
∵EB=ME+MB,MB=BN+NM=4(cm),
19.(1)∵四边形ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°.
∴AB=DE.∴△ABE∽△DEF.
(2)∵四边形ABCD为正方形,
正方形的边长为4,∴ED=2,CG=6.
∴BG=BC+CG=10.
20.(1)△FBG △F BG
即
∴GM=16(m).
∴BG=13.5(m).∴AB=BG+GA=15(m).
∴电线杆 AB 的高度为15m.
21.(1)∵AB是⊙O的直径,∴∠ADB=90°.
∵AB=BC,∴D是AC 的中点,∠ABD=∠CBD.
∴AD=DE.
(2)∵四边形 ABED内接于⊙O,∴∠CED=∠CAB.
∵∠C=∠C,∴△CED∽△CAB.∴CA=CD.
∵AB=BC=10,CE=2,D是AC 的中点,.
(3)如答图所示,延长 EF 交⊙O于点M.BE=BC-CE=10-2=8,在 Rt△ABD中,
∵EM⊥AB,AB是⊙O的直径,
∴∠BEP=∠EDB.∴△BPE∽△BED.
,
22.(1)存在点 P.假设存在一点 P,使点 Q与点C 重合,如答图1所示,设AP 的长为x,则 BP=10-x.
在Rt△APD中,
在 Rt△PBC中,
在Rt△PCD 中, 即 (10-x) ,解得x=2或8.
故当m=10时,存在点 P 使得点 Q 与点C 重合,此时AP=2或8.
(2)连结AC,设BP=y,则AP=m-y.
∵PQ∥AC,∴△PBQ∽△ABC.
即
∵DP⊥PQ,∴∠APD+∠BPQ=90°.
∵∠BPQ+∠BQP=90°,
∴∠APD=∠BQP.∴△APD∽△BQP.
即
(3)①当点 Q在BC 上时,如答图3所示,连结 DQ.
∵PQ⊥PD,∴只有当 DP=PQ时,△PQD 为等腰三角形.
∵△APD∽△BQP,∴△BQP≌△APD.
∴PB=DA=4,AP=BQ=m-4.
∴以点 P,Q,C,D为顶点的四边形的面积S=S矩形ABCD一 =16(m≤8).
②当点 Q在BC 延长线上时,如答图4 所示,连结 DQ,PC.
∵DP=PQ,∴△DAP≌△PBQ.∴PB=AD=4,AB=BQ=m-4.
23.(1)如答图所示,过点 A 作AG∥MN 交 BN 延长线于点G.
∴∠G=∠BNM.又∵∠B=∠B,∴△ABG∽△MBN.
即
同理,在△ACG和△OCN 中,
∵O为AC 中点,∴AO=CO.∴NG=CN.
(2)由(1)知
(3)在△ABD 中,P 是AD 上的一点,过点 P 的直线与AB 及BD 的延长线分别相交于点 F,C,
由(2)得
在△ACD中,P 是AD 上一点,过点 P 的直线与AC 及CD 的延长线分别相交于点E,B,
由(2)得
同课章节目录
