专题复习一 线段比例关系的证明和应用提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 专题复习一 线段比例关系的证明和应用提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 282.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:32:05 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题复习一 线段比例关系的证明和应用
基础巩固
如图所示,在△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为中线,若AD=5,CD=3,DE=4,则 BF的
长为( ).
A. B. C. D.
2.如图所示,弦AB和CD 相交于⊙O内一点 P,则下列结论中,不一定成立的是( ).
B. PA·PD=PB·PC
D. PA·PB=PC·PD
3.如图所示,在△ABC中,AD是角平分线,∠ADE=∠B,若AE=4,AB=5,则AD的长为 .
4.如图所示,在Rt△ABC中,∠C=90°,D是AB 上一点,作 DE⊥BC于点E,连结AE,若 ,则AE的长为 .
5.如图所示,在△ABC中,点 D,E分别在边AB,AC上,∠AED=∠B,射线 AG分别交线段DE,BC于点F,G,且
(1)求证:△ADF∽△ACG.
(2)若 求 的值.
6.如图所示,⊙O是△ABC的外接圆,BC是⊙O的直径,D是 的中点,BD 交 AC于点E,连结AD,CD.
(1)求证:
(2)若 求 DE 的长.
能力提升
7.如图所示,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式为( ).
A. b=a+c B. b= ac D. b=2a=2c
如图所示,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC,BD交于点E,且AB=BD,EC=1,则AD
的长为( ).
B. C. D.3
9.如图所示,在四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB 于点E,且BE=CE.若BC=6,AC=4,则 BD的长为 .
10.如图所示,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD 相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B 和点F.
(1)求证:∠ADF=∠EAC.
(2)若 求AF 的长.
11.如图所示,点P 在以 MN为直径的半圆上运动(点P 不与点 M,N重合),PQ⊥MN,NE平分∠MNP,交 PM于点 E,交 PQ于点 F.
(2)若 则
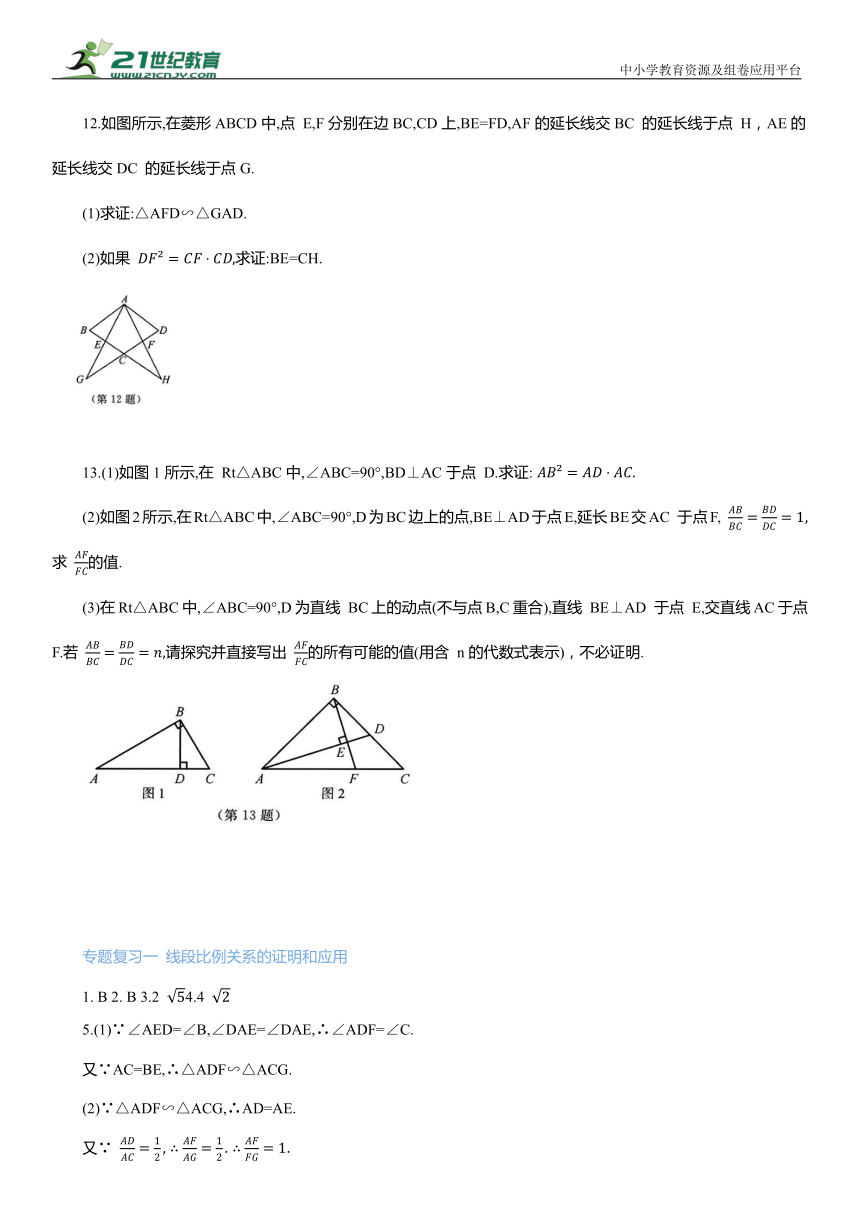
12.如图所示,在菱形ABCD中,点 E,F分别在边BC,CD上,BE=FD,AF的延长线交BC 的延长线于点 H,AE的延长线交DC 的延长线于点G.
(1)求证:△AFD∽△GAD.
(2)如果 求证:BE=CH.
13.(1)如图1所示,在 Rt△ABC中,∠ABC=90°,BD⊥AC于点 D.求证:
(2)如图2所示,在Rt△ABC中,∠ABC=90°,D为BC边上的点,BE⊥AD于点E,延长BE交AC 于点F, 求 的值.
(3)在Rt△ABC中,∠ABC=90°,D为直线 BC上的动点(不与点B,C重合),直线 BE⊥AD 于点 E,交直线AC于点 F.若 请探究并直接写出 的所有可能的值(用含 n的代数式表示),不必证明.
专题复习一 线段比例关系的证明和应用
1. B 2. B 3.2 4.4
5.(1)∵∠AED=∠B,∠DAE=∠DAE,∴∠ADF=∠C.
又∵AC=BE,∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,∴AD=AE.
又∵
6.(1)∵D是AC的中点,∴AD=DC.∴∠ABD=∠DAC.
又∵∠ADB=∠EDA,∴△ABD∽△EAD.
(2)∵D是AC的中点,.
∵CB是直径,∴△BCD 是直角三角形.
解得
7. A 8. A 9.2
10.(1)∵∠ADC=90°,∠ACE=90°,
∴∠ADF+∠FDC=90°,∠EAC+∠CEF=90°.
∵∠FDC=∠CEF,∴∠ADF=∠EAC.
(2)如答图所示,连结 FC.
∵CD是圆O的直径,
∴∠DFC=90°.
∴∠FDC+∠FCD=90°.
∵∠ADF+∠FDC=90°,∠ADF=∠EAC,
∴∠FCD=∠EAC,即∠FCP=∠CAP.
又∵∠FPC=∠CPA,∴△FPC∽△CPA.∴PE=PCPA.
解得
即
11.(1)1
【解析】(1)∵MN为⊙O的直径,∴∠MPN=90°.
∵PQ⊥MN,∴∠PQN=∠MPN=90°.
∵NE平分∠PNM,∴∠MNE=∠PNE.
∴△PEN∽△QFN.. 即
∵∠PNQ+∠NPQ=∠PNQ+∠PMQ=90°,
∴∠NPQ=∠PMQ.
∵∠PQN=∠PQM=90°,∴△NPQ∽△PMQ.
∴M=NO②.∴①×②得
(2)∵∠PNQ=∠MNP,∠NQP=∠NPM,
∵PN =PM·MN,∴PM=QN.∴MO=MPN.
∵∠MPN=90°,∠MQP=90°,∴△MPN∽△MQP.
即
设 则
解得 或 舍去).
12.(1)∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.
又∵BE=DF,∴△ABE≌△ADF.∴∠BAE=∠DAF.
∵AB∥CD,∴∠G=∠BAE=∠DAF.
又∵∠D=∠D,∴△AFD∽△GAD.
∵AD=CD,∴CH=DF.
∵BE=DF,∴BE=CH.
13.(1)∵BD⊥AC,∠ABC=90°,∴∠ADB=∠ABC.
∵∠A=∠A,∴△ADB∽△ABC.
(2)如答图所示,过点 C作CG⊥AD交AD 的延长线于点G.
∵BE⊥AD,∴∠CGD=∠BED=90°,CG∥BF.
∴AB=BC=2BD=2DC,BD=DC.
∵∠BDE=∠CDG,∴△BDE≌△CDG.
由(1)可得:AB =AE·AD,BD =DE·AD,
(3)D为直线BC 上的动点(不与点 B,C重合),有三种情况:
①当点 D 在线段BC 上时
②当点 D 在线段BC 的延长线上时,
③当点 D 在线段CB 的延长线上时,
专题复习一 线段比例关系的证明和应用
基础巩固
如图所示,在△ABC中,D,E分别为AC,BC边上的点,AB∥DE,CF为中线,若AD=5,CD=3,DE=4,则 BF的
长为( ).
A. B. C. D.
2.如图所示,弦AB和CD 相交于⊙O内一点 P,则下列结论中,不一定成立的是( ).
B. PA·PD=PB·PC
D. PA·PB=PC·PD
3.如图所示,在△ABC中,AD是角平分线,∠ADE=∠B,若AE=4,AB=5,则AD的长为 .
4.如图所示,在Rt△ABC中,∠C=90°,D是AB 上一点,作 DE⊥BC于点E,连结AE,若 ,则AE的长为 .
5.如图所示,在△ABC中,点 D,E分别在边AB,AC上,∠AED=∠B,射线 AG分别交线段DE,BC于点F,G,且
(1)求证:△ADF∽△ACG.
(2)若 求 的值.
6.如图所示,⊙O是△ABC的外接圆,BC是⊙O的直径,D是 的中点,BD 交 AC于点E,连结AD,CD.
(1)求证:
(2)若 求 DE 的长.
能力提升
7.如图所示,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式为( ).
A. b=a+c B. b= ac D. b=2a=2c
如图所示,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC,BD交于点E,且AB=BD,EC=1,则AD
的长为( ).
B. C. D.3
9.如图所示,在四边形ADBC中,∠ADB=∠ACB,CD平分∠ACB交AB 于点E,且BE=CE.若BC=6,AC=4,则 BD的长为 .
10.如图所示,△ACE,△ACD均为直角三角形,∠ACE=90°,∠ADC=90°,AE与CD 相交于点P,以CD为直径的⊙O恰好经过点E,并与AC,AE分别交于点B 和点F.
(1)求证:∠ADF=∠EAC.
(2)若 求AF 的长.
11.如图所示,点P 在以 MN为直径的半圆上运动(点P 不与点 M,N重合),PQ⊥MN,NE平分∠MNP,交 PM于点 E,交 PQ于点 F.
(2)若 则
12.如图所示,在菱形ABCD中,点 E,F分别在边BC,CD上,BE=FD,AF的延长线交BC 的延长线于点 H,AE的延长线交DC 的延长线于点G.
(1)求证:△AFD∽△GAD.
(2)如果 求证:BE=CH.
13.(1)如图1所示,在 Rt△ABC中,∠ABC=90°,BD⊥AC于点 D.求证:
(2)如图2所示,在Rt△ABC中,∠ABC=90°,D为BC边上的点,BE⊥AD于点E,延长BE交AC 于点F, 求 的值.
(3)在Rt△ABC中,∠ABC=90°,D为直线 BC上的动点(不与点B,C重合),直线 BE⊥AD 于点 E,交直线AC于点 F.若 请探究并直接写出 的所有可能的值(用含 n的代数式表示),不必证明.
专题复习一 线段比例关系的证明和应用
1. B 2. B 3.2 4.4
5.(1)∵∠AED=∠B,∠DAE=∠DAE,∴∠ADF=∠C.
又∵AC=BE,∴△ADF∽△ACG.
(2)∵△ADF∽△ACG,∴AD=AE.
又∵
6.(1)∵D是AC的中点,∴AD=DC.∴∠ABD=∠DAC.
又∵∠ADB=∠EDA,∴△ABD∽△EAD.
(2)∵D是AC的中点,.
∵CB是直径,∴△BCD 是直角三角形.
解得
7. A 8. A 9.2
10.(1)∵∠ADC=90°,∠ACE=90°,
∴∠ADF+∠FDC=90°,∠EAC+∠CEF=90°.
∵∠FDC=∠CEF,∴∠ADF=∠EAC.
(2)如答图所示,连结 FC.
∵CD是圆O的直径,
∴∠DFC=90°.
∴∠FDC+∠FCD=90°.
∵∠ADF+∠FDC=90°,∠ADF=∠EAC,
∴∠FCD=∠EAC,即∠FCP=∠CAP.
又∵∠FPC=∠CPA,∴△FPC∽△CPA.∴PE=PCPA.
解得
即
11.(1)1
【解析】(1)∵MN为⊙O的直径,∴∠MPN=90°.
∵PQ⊥MN,∴∠PQN=∠MPN=90°.
∵NE平分∠PNM,∴∠MNE=∠PNE.
∴△PEN∽△QFN.. 即
∵∠PNQ+∠NPQ=∠PNQ+∠PMQ=90°,
∴∠NPQ=∠PMQ.
∵∠PQN=∠PQM=90°,∴△NPQ∽△PMQ.
∴M=NO②.∴①×②得
(2)∵∠PNQ=∠MNP,∠NQP=∠NPM,
∵PN =PM·MN,∴PM=QN.∴MO=MPN.
∵∠MPN=90°,∠MQP=90°,∴△MPN∽△MQP.
即
设 则
解得 或 舍去).
12.(1)∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.
又∵BE=DF,∴△ABE≌△ADF.∴∠BAE=∠DAF.
∵AB∥CD,∴∠G=∠BAE=∠DAF.
又∵∠D=∠D,∴△AFD∽△GAD.
∵AD=CD,∴CH=DF.
∵BE=DF,∴BE=CH.
13.(1)∵BD⊥AC,∠ABC=90°,∴∠ADB=∠ABC.
∵∠A=∠A,∴△ADB∽△ABC.
(2)如答图所示,过点 C作CG⊥AD交AD 的延长线于点G.
∵BE⊥AD,∴∠CGD=∠BED=90°,CG∥BF.
∴AB=BC=2BD=2DC,BD=DC.
∵∠BDE=∠CDG,∴△BDE≌△CDG.
由(1)可得:AB =AE·AD,BD =DE·AD,
(3)D为直线BC 上的动点(不与点 B,C重合),有三种情况:
①当点 D 在线段BC 上时
②当点 D 在线段BC 的延长线上时,
③当点 D 在线段CB 的延长线上时,
同课章节目录
