4.7 图形的位似 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.7 图形的位似 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 398.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:31:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
4.7 图形的位似
基础巩固
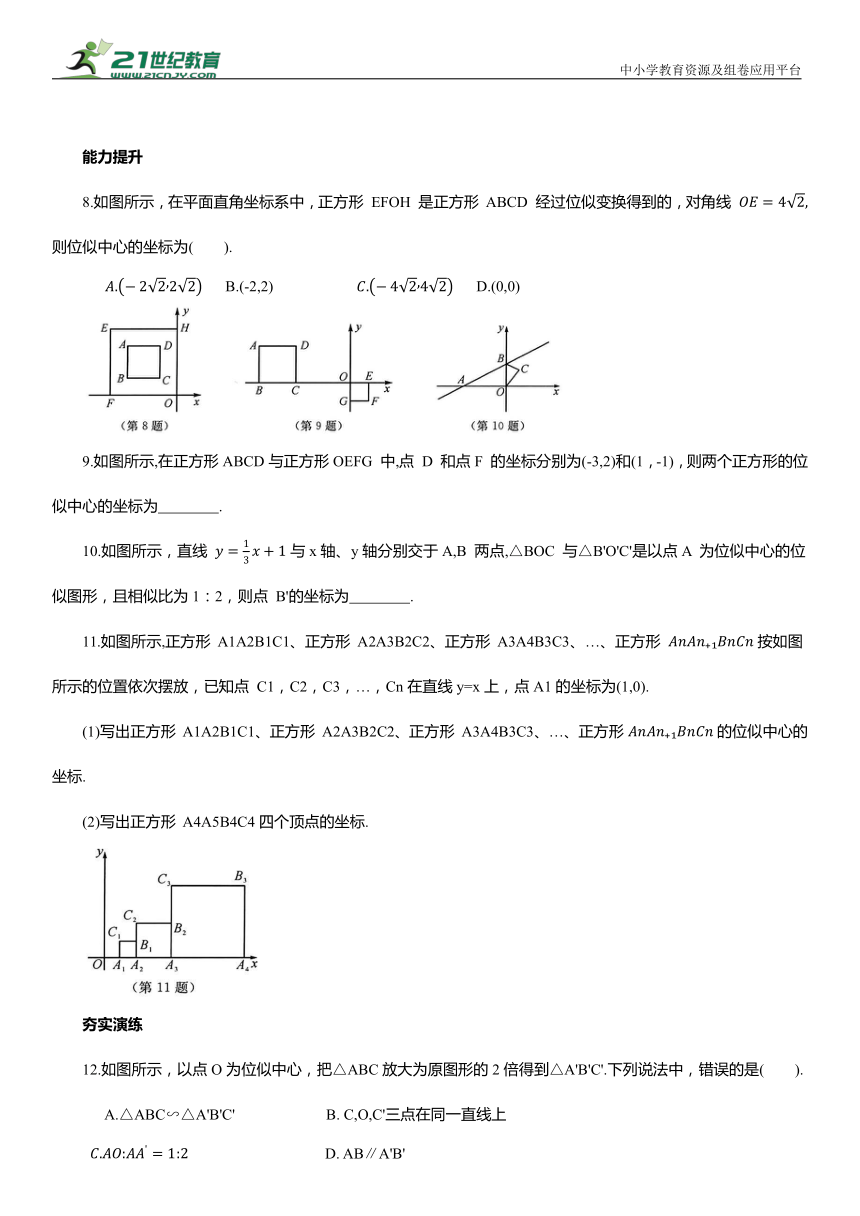
1.如图所示,△ABC 与△DEF 是位似图形,点O是位似中心,OA=AD,则△ABC与△DEF 的位似比是( ).
A. B. C.2 D.3
2.如图所示,五边形ABCDE是由五边形FGHMN 经过位似变换得到的,点O是位似中心,F,G,H,M,N分别是OA,OB,OC,OD,OE的中点,则五边形 ABCDE 与五边形FGHMN 的面积比是( ).
A.6:1 B.5:1 C.4:1 D.2: 1
3.下列图形中,△ABC∽△DEF,则这两个三角形不是位似图形的为( ).
4.如图所示,△A'B'C'是将△ABC放大后的图形,若 则S△A'B'C' = .
5.如图所示,五边形 ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为 ,若五边形ABCDE 的面积为18cm ,周长为21cm,则五边形A'B'C'D'E'的面积为 cm ,周长为 cm.
6.在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'位似,位似中心为原点O,点A的坐标为(-2,1),它的对应点 A'(1,-0.5),若AB=2,则
7.如图所示,在边长为1个单位的小正方形组成的网格中,按要求画出△A B C 和△A B C .
(1)以点O为位似中心,在点O的同侧作△A B C ,使它与原三角形的位似比为1:2.
(2)将△ABC 绕点 O 按顺时针方向旋转 90°后得到△A B C ,则点 A 旋转的路径长为 .
能力提升
8.如图所示,在平面直角坐标系中,正方形 EFOH 是正方形 ABCD 经过位似变换得到的,对角线 则位似中心的坐标为( ).
B.(-2,2) D.(0,0)
9.如图所示,在正方形ABCD与正方形OEFG 中,点 D 和点F 的坐标分别为(-3,2)和(1,-1),则两个正方形的位似中心的坐标为 .
10.如图所示,直线 与x轴、y轴分别交于A,B 两点,△BOC 与△B'O'C'是以点A 为位似中心的位似图形,且相似比为1:2,则点 B'的坐标为 .
11.如图所示,正方形 A1A2B1C1、正方形 A2A3B2C2、正方形 A3A4B3C3、…、正方形 按如图所示的位置依次摆放,已知点 C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形 A1A2B1C1、正方形 A2A3B2C2、正方形 A3A4B3C3、…、正方形的位似中心的坐标.
(2)写出正方形 A4A5B4C4四个顶点的坐标.
夯实演练
12.如图所示,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C'.下列说法中,错误的是( ).
A.△ABC∽△A'B'C' B. C,O,C'三点在同一直线上
D. AB∥A'B'
13.如图所示,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,若点A(2,2),B(3,4),C(6,1),B'(6,8),则△A'B'C'的面积为 .
14.如图所示,正三角形ABC的边长为3
(1)如图1所示,正方形 EFPN的顶点 E,F在边 AB上,顶点 N在边 AC上,在正三角形ABC及其内部,以点A 为位似中心,作正方形 EFPN 的位似正方形E'F'P'N',且使正方形E'F'P'N'的面积最大(不要求写作法).
(2)求(1)中作出的正方形 E'F'P'N'的边长.
(3)如图2所示,在正三角形ABC中放入正方形DEMN 和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
12.如图所示,在菱形 ABCD中,∠ADC=60°,点 E,F 分别在AD,CD上,且AE=DF,AF 与CE 相交于点G,BG与AC相交于点 H.现有下列结论:①△ACF≌△CDE;②CG =GH·BG;③若 DF=2CF,则 其中,正确的结论有 (填序号).
13.如图所示,将一副斜边相等的三角尺按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,O为斜边AB 的中点,连结CD交AB 于点E.
(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
(2)求证:CD平分∠ACB.
(3)过点 D 作DF∥BC交AB 于点F,求证:
14.在△ABC中,P 为边AB 上一点.
(1)如图1所示,若∠ACP=∠B,求证:AC =AP·AB.
(2)若M为CP 的中点,AC=2.
①如图2所示,若∠PBM=∠ACP,AB=3,求 BP 的长.
②如图3所示,若∠ABC=45°,∠A=∠BMP=60°,求BP 的长.
4.7 图形的位似
1. A 2. C 3. B 4. 5.8 14 6.1
7.(1)图略
8. B 9.(-1,0)或(5,-2) 10.(3,2)或(-9,-2)
11.(1) 如 答 图 所示, 正 方形 A A B C 、正 方 形A A B C 、正方形 A A B C 、…、正方形 A A B C 的位似中心的坐标为(0,0).
(2)∵点 C ,C ,C ,…, Cn在直线y=x上,点 A 的坐标为(1,0),
则
则
∴A (8,0),A (16,0),B (16,8),C (8,8).
12. C 13.18
14.(1)如答图1所示,正方形 E'F'P'N'即为所求.
(2)设正方形 E'F'P'N'的边长为x.
∵△ABC为正三角形,
解得
(3)如答图2 所示,连结 NE,EP,PN,延长 PH 交 ND于点G,则 PG⊥ND,∠NEP=90°.
设正方形 DEMN,正方形 EFPH 的边长分别为 m,n(m≥n),它们的面积和为 S,则
在 Rt△PGN中,
∵AD+DE+EF+BF=AB,
①当( ,即m=n时,S最小.
②当(m-n) 最大,即当m最大且n最小时,S最大.
∵m+n=3,由(2)知,
综上所述
4.7 图形的位似
基础巩固
1.如图所示,△ABC 与△DEF 是位似图形,点O是位似中心,OA=AD,则△ABC与△DEF 的位似比是( ).
A. B. C.2 D.3
2.如图所示,五边形ABCDE是由五边形FGHMN 经过位似变换得到的,点O是位似中心,F,G,H,M,N分别是OA,OB,OC,OD,OE的中点,则五边形 ABCDE 与五边形FGHMN 的面积比是( ).
A.6:1 B.5:1 C.4:1 D.2: 1
3.下列图形中,△ABC∽△DEF,则这两个三角形不是位似图形的为( ).
4.如图所示,△A'B'C'是将△ABC放大后的图形,若 则S△A'B'C' = .
5.如图所示,五边形 ABCDE与五边形A'B'C'D'E'是位似图形,且位似比为 ,若五边形ABCDE 的面积为18cm ,周长为21cm,则五边形A'B'C'D'E'的面积为 cm ,周长为 cm.
6.在平面直角坐标系中,四边形ABCD与四边形A'B'C'D'位似,位似中心为原点O,点A的坐标为(-2,1),它的对应点 A'(1,-0.5),若AB=2,则
7.如图所示,在边长为1个单位的小正方形组成的网格中,按要求画出△A B C 和△A B C .
(1)以点O为位似中心,在点O的同侧作△A B C ,使它与原三角形的位似比为1:2.
(2)将△ABC 绕点 O 按顺时针方向旋转 90°后得到△A B C ,则点 A 旋转的路径长为 .
能力提升
8.如图所示,在平面直角坐标系中,正方形 EFOH 是正方形 ABCD 经过位似变换得到的,对角线 则位似中心的坐标为( ).
B.(-2,2) D.(0,0)
9.如图所示,在正方形ABCD与正方形OEFG 中,点 D 和点F 的坐标分别为(-3,2)和(1,-1),则两个正方形的位似中心的坐标为 .
10.如图所示,直线 与x轴、y轴分别交于A,B 两点,△BOC 与△B'O'C'是以点A 为位似中心的位似图形,且相似比为1:2,则点 B'的坐标为 .
11.如图所示,正方形 A1A2B1C1、正方形 A2A3B2C2、正方形 A3A4B3C3、…、正方形 按如图所示的位置依次摆放,已知点 C1,C2,C3,…,Cn在直线y=x上,点A1的坐标为(1,0).
(1)写出正方形 A1A2B1C1、正方形 A2A3B2C2、正方形 A3A4B3C3、…、正方形的位似中心的坐标.
(2)写出正方形 A4A5B4C4四个顶点的坐标.
夯实演练
12.如图所示,以点O为位似中心,把△ABC放大为原图形的2倍得到△A'B'C'.下列说法中,错误的是( ).
A.△ABC∽△A'B'C' B. C,O,C'三点在同一直线上
D. AB∥A'B'
13.如图所示,△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形,若点A(2,2),B(3,4),C(6,1),B'(6,8),则△A'B'C'的面积为 .
14.如图所示,正三角形ABC的边长为3
(1)如图1所示,正方形 EFPN的顶点 E,F在边 AB上,顶点 N在边 AC上,在正三角形ABC及其内部,以点A 为位似中心,作正方形 EFPN 的位似正方形E'F'P'N',且使正方形E'F'P'N'的面积最大(不要求写作法).
(2)求(1)中作出的正方形 E'F'P'N'的边长.
(3)如图2所示,在正三角形ABC中放入正方形DEMN 和正方形EFPH,使得DE,EF在边AB上,点P,N分别在边CB,CA上,求这两个正方形面积和的最大值和最小值,并说明理由.
12.如图所示,在菱形 ABCD中,∠ADC=60°,点 E,F 分别在AD,CD上,且AE=DF,AF 与CE 相交于点G,BG与AC相交于点 H.现有下列结论:①△ACF≌△CDE;②CG =GH·BG;③若 DF=2CF,则 其中,正确的结论有 (填序号).
13.如图所示,将一副斜边相等的三角尺按斜边重合摆放在同一平面内,其中∠CAB=30°,∠DAB=45°,O为斜边AB 的中点,连结CD交AB 于点E.
(1)求证:A,B,C,D四个点在以点O为圆心的同一个圆上.
(2)求证:CD平分∠ACB.
(3)过点 D 作DF∥BC交AB 于点F,求证:
14.在△ABC中,P 为边AB 上一点.
(1)如图1所示,若∠ACP=∠B,求证:AC =AP·AB.
(2)若M为CP 的中点,AC=2.
①如图2所示,若∠PBM=∠ACP,AB=3,求 BP 的长.
②如图3所示,若∠ABC=45°,∠A=∠BMP=60°,求BP 的长.
4.7 图形的位似
1. A 2. C 3. B 4. 5.8 14 6.1
7.(1)图略
8. B 9.(-1,0)或(5,-2) 10.(3,2)或(-9,-2)
11.(1) 如 答 图 所示, 正 方形 A A B C 、正 方 形A A B C 、正方形 A A B C 、…、正方形 A A B C 的位似中心的坐标为(0,0).
(2)∵点 C ,C ,C ,…, Cn在直线y=x上,点 A 的坐标为(1,0),
则
则
∴A (8,0),A (16,0),B (16,8),C (8,8).
12. C 13.18
14.(1)如答图1所示,正方形 E'F'P'N'即为所求.
(2)设正方形 E'F'P'N'的边长为x.
∵△ABC为正三角形,
解得
(3)如答图2 所示,连结 NE,EP,PN,延长 PH 交 ND于点G,则 PG⊥ND,∠NEP=90°.
设正方形 DEMN,正方形 EFPH 的边长分别为 m,n(m≥n),它们的面积和为 S,则
在 Rt△PGN中,
∵AD+DE+EF+BF=AB,
①当( ,即m=n时,S最小.
②当(m-n) 最大,即当m最大且n最小时,S最大.
∵m+n=3,由(2)知,
综上所述
同课章节目录
