4.4 两个三角形相似的判定(2)提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.4 两个三角形相似的判定(2)提优训练(含答案)2024-2025学年浙教版九年级数学上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 303.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:37:01 | ||
图片预览



文档简介
4.4 两个三角形相似的判定(2)
基础巩固
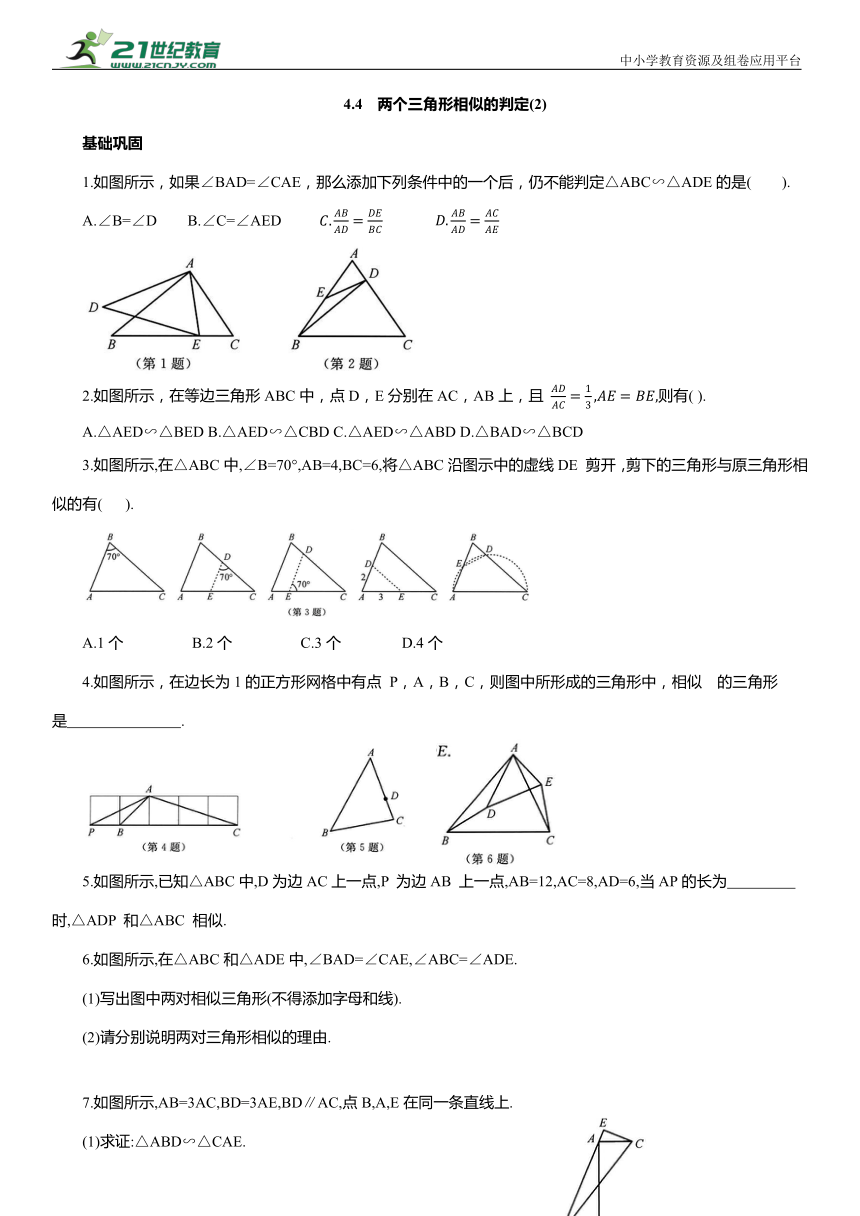
1.如图所示,如果∠BAD=∠CAE,那么添加下列条件中的一个后,仍不能判定△ABC∽△ADE的是( ).
A.∠B=∠D B.∠C=∠AED
2.如图所示,在等边三角形ABC中,点D,E分别在AC,AB上,且 则有( ).
A.△AED∽△BED B.△AED∽△CBD C.△AED∽△ABD D.△BAD∽△BCD
3.如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE 剪开,剪下的三角形与原三角形相似的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,在边长为1的正方形网格中有点 P,A,B,C,则图中所形成的三角形中,相似 的三角形是 .
5.如图所示,已知△ABC中,D为边AC上一点,P 为边AB 上一点,AB=12,AC=8,AD=6,当AP的长为 时,△ADP 和△ABC 相似.
6.如图所示,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请分别说明两对三角形相似的理由.
7.如图所示,AB=3AC,BD=3AE,BD∥AC,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE.
(2)如果AC=BD,AD=2 BD,设BD=a,求BC的长.
能力提升
8.如图所示,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD交于点C.要使△ADC与△ABD相似,可以添加一个条件.下列条件中,添加后错误的是( ).
A.∠ACD=∠DAB B. AD=DE
D. CD·AB=AC·BD
9.如图所示,P 为∠MON平分线OC 上一点,以点 P 为顶点的∠APB的两边分别与射线OM,ON 相交于点A,B.如果∠APB 在绕点 P 旋转时始终满足OA·OB=OP ,我们就把∠APB 叫做∠MON的“关联角”.如果∠MON=50°,∠APB 是∠MON 的“关联角”,那么∠APB的度数为 .
10.如图所示,在 ABCD中,AB=4,AD=6,∠ABC=60°,P是射线AD上的一个动点(与点A 不重合),BP与AC 交于点E.设AP=x,当x= 时,△ABP 与△EBC相似.
11.如图所示,已知 是三个全等的等腰三角形;底边 BC,CE,EG在同一条直线上,且 连结 BF 分别交AC,DC,DE于点 P,Q,R.
(1)求证: 并求出BF 的长.
(2)观察图形,请你提出一个与点 P 相关的数学问题,并进行解答.
12.如图所示,已知点 D,E分别在△ABC的边AC,BC上,线段 BD与AE 交于点F,且CD·CA=CE·CB.
(1)求证:∠CAE=∠CBD.
(2)若 求证:AB·AD=AF·AE.
夯实演练
13.如图所示,在正方形ABCD中,F是BC 边上一点,连结AF,以AF为对角线作正方形AEFG,边 FG与正方形ABCD的对角线 AC 相交于点 H,连结 DG.现有以下四个结论:①∠EAB=∠GAD;②△AFC∽△AGD;③2AE =AH·AC;④DG⊥AC.其中,正确的有( ).
A.1个 B.2个
C.3个 D.4个
14.如图所示,在△ABC中,AB=AC,点 E 在边BC 上移动(点E 不与点B,C重合),满足∠DEF=∠B,且点 D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF.
(2)当点 E 移动到BC 的中点时,求证:FE平分∠DFC.
15.如图所示,在矩形ABCD中, 点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动.点E,G的速度均为2cm/s,点F 的速度为4cm/s.当点 F 追上点G(即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t(s)时,△EFG的面积为
(1)当t=1(s)时,S的值是多少
(2)写出S关于t 的函数表达式,并指出自变量t的取值范围.
(3)若点 F 在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似 请说明理由.
4.4 两个三角形相似的判定(1)
1. C 2. D 3. A 4.4 5.2
6.在△ABC中,∵AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,∴∠ADB=∠CEB=90°.
∵∠B=∠B,∴△ABD∽△CBE.
7.(1)∵∠AEC=∠DEB,∠ACE=∠DBE,∴△AEC∽△DEB.
(2)设⊙O的半径为r,则CE=2r-2.
∵CD⊥AB,AB=8,∴AE=BE= AB=4.
∵△AEC∽△DEB,
即 解得r=5.
8. C 9. B 10.
11.(1)∵四边形ABCD 是正方形,
∴∠ADH=90°,AD=DC.
∵FG⊥CD,∴∠FGH=90°.∴∠ADH=∠FGH.
又∵∠AHD=∠FHG,∴△ADH∽△FGH.
(2)∵FG⊥CD,DC⊥BE,FE⊥BE,
∴四边形 CEFG 是矩形.
又∵DH=CH,∴CG=2GH.
∴矩形 CEFG是正方形.
12.(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∵CD平分∠ACB,
∴∠ACD=∠FCB=45°.
∵AE⊥CD,
∵∠E=∠ABC,
∴△ACE∽△CFB.
(2)如答图所示,延长AE,CB交于点 M.
∵∠FCB=45°,∠CHM=90°,∴∠M=45°=∠CAE.
∴HA=HC=HM,CM=CA=6.
∵CB=4,∴BM=6-4=2.
∵OA=OB,HA=HM,∴OH是△ABM的中位线.
13.
14.(1)∵四边形 ABCD是矩形,∴AD∥BC,∠B=90°.
∴∠DAF=∠AEB.
∵DF⊥AE,∴∠AFD=∠B=90°.∴△ABE∽△DFA.
(2)∵E是BC 的中点,BC=4,∴BE=2.
∵四边形ABCD是矩形,∴AD=BC=4.
∵△ABE∽△DFA,∴ABF=AED.
中小学教育资源及组卷应用平台
15.(1)∵Rt△AB'C'是由 Rt△ABC绕点 A 按顺时针方向旋转得到的,∴ AC= AC',AB = AB',∠CAB =∠C'AB'.
,即∠CAC'=∠BAB'.
∵∠AEC=∠FEB,∴△ACE∽△FBE.
(2)当β=2α时,△ACE≌△FBE.
即
∴∠BCE=α.
∵∠ABC=α,∴∠ABC=∠BCE.∴CE=BE.
∵△ACE∽△FBE,
∴∠BEF=∠CEA,∠FBE=∠ACE.
∵CE=BE,∴△ACE≌△FBE.
基础巩固
1.如图所示,如果∠BAD=∠CAE,那么添加下列条件中的一个后,仍不能判定△ABC∽△ADE的是( ).
A.∠B=∠D B.∠C=∠AED
2.如图所示,在等边三角形ABC中,点D,E分别在AC,AB上,且 则有( ).
A.△AED∽△BED B.△AED∽△CBD C.△AED∽△ABD D.△BAD∽△BCD
3.如图所示,在△ABC中,∠B=70°,AB=4,BC=6,将△ABC沿图示中的虚线DE 剪开,剪下的三角形与原三角形相似的有( ).
A.1个 B.2个 C.3个 D.4个
4.如图所示,在边长为1的正方形网格中有点 P,A,B,C,则图中所形成的三角形中,相似 的三角形是 .
5.如图所示,已知△ABC中,D为边AC上一点,P 为边AB 上一点,AB=12,AC=8,AD=6,当AP的长为 时,△ADP 和△ABC 相似.
6.如图所示,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线).
(2)请分别说明两对三角形相似的理由.
7.如图所示,AB=3AC,BD=3AE,BD∥AC,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE.
(2)如果AC=BD,AD=2 BD,设BD=a,求BC的长.
能力提升
8.如图所示,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD交于点C.要使△ADC与△ABD相似,可以添加一个条件.下列条件中,添加后错误的是( ).
A.∠ACD=∠DAB B. AD=DE
D. CD·AB=AC·BD
9.如图所示,P 为∠MON平分线OC 上一点,以点 P 为顶点的∠APB的两边分别与射线OM,ON 相交于点A,B.如果∠APB 在绕点 P 旋转时始终满足OA·OB=OP ,我们就把∠APB 叫做∠MON的“关联角”.如果∠MON=50°,∠APB 是∠MON 的“关联角”,那么∠APB的度数为 .
10.如图所示,在 ABCD中,AB=4,AD=6,∠ABC=60°,P是射线AD上的一个动点(与点A 不重合),BP与AC 交于点E.设AP=x,当x= 时,△ABP 与△EBC相似.
11.如图所示,已知 是三个全等的等腰三角形;底边 BC,CE,EG在同一条直线上,且 连结 BF 分别交AC,DC,DE于点 P,Q,R.
(1)求证: 并求出BF 的长.
(2)观察图形,请你提出一个与点 P 相关的数学问题,并进行解答.
12.如图所示,已知点 D,E分别在△ABC的边AC,BC上,线段 BD与AE 交于点F,且CD·CA=CE·CB.
(1)求证:∠CAE=∠CBD.
(2)若 求证:AB·AD=AF·AE.
夯实演练
13.如图所示,在正方形ABCD中,F是BC 边上一点,连结AF,以AF为对角线作正方形AEFG,边 FG与正方形ABCD的对角线 AC 相交于点 H,连结 DG.现有以下四个结论:①∠EAB=∠GAD;②△AFC∽△AGD;③2AE =AH·AC;④DG⊥AC.其中,正确的有( ).
A.1个 B.2个
C.3个 D.4个
14.如图所示,在△ABC中,AB=AC,点 E 在边BC 上移动(点E 不与点B,C重合),满足∠DEF=∠B,且点 D,F分别在边AB,AC上.
(1)求证:△BDE∽△CEF.
(2)当点 E 移动到BC 的中点时,求证:FE平分∠DFC.
15.如图所示,在矩形ABCD中, 点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方向移动.点E,G的速度均为2cm/s,点F 的速度为4cm/s.当点 F 追上点G(即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t(s)时,△EFG的面积为
(1)当t=1(s)时,S的值是多少
(2)写出S关于t 的函数表达式,并指出自变量t的取值范围.
(3)若点 F 在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似 请说明理由.
4.4 两个三角形相似的判定(1)
1. C 2. D 3. A 4.4 5.2
6.在△ABC中,∵AB=AC,BD=CD,∴AD⊥BC.
∵CE⊥AB,∴∠ADB=∠CEB=90°.
∵∠B=∠B,∴△ABD∽△CBE.
7.(1)∵∠AEC=∠DEB,∠ACE=∠DBE,∴△AEC∽△DEB.
(2)设⊙O的半径为r,则CE=2r-2.
∵CD⊥AB,AB=8,∴AE=BE= AB=4.
∵△AEC∽△DEB,
即 解得r=5.
8. C 9. B 10.
11.(1)∵四边形ABCD 是正方形,
∴∠ADH=90°,AD=DC.
∵FG⊥CD,∴∠FGH=90°.∴∠ADH=∠FGH.
又∵∠AHD=∠FHG,∴△ADH∽△FGH.
(2)∵FG⊥CD,DC⊥BE,FE⊥BE,
∴四边形 CEFG 是矩形.
又∵DH=CH,∴CG=2GH.
∴矩形 CEFG是正方形.
12.(1)∵AB是⊙O的直径,
∴∠ACB=90°.
∵CD平分∠ACB,
∴∠ACD=∠FCB=45°.
∵AE⊥CD,
∵∠E=∠ABC,
∴△ACE∽△CFB.
(2)如答图所示,延长AE,CB交于点 M.
∵∠FCB=45°,∠CHM=90°,∴∠M=45°=∠CAE.
∴HA=HC=HM,CM=CA=6.
∵CB=4,∴BM=6-4=2.
∵OA=OB,HA=HM,∴OH是△ABM的中位线.
13.
14.(1)∵四边形 ABCD是矩形,∴AD∥BC,∠B=90°.
∴∠DAF=∠AEB.
∵DF⊥AE,∴∠AFD=∠B=90°.∴△ABE∽△DFA.
(2)∵E是BC 的中点,BC=4,∴BE=2.
∵四边形ABCD是矩形,∴AD=BC=4.
∵△ABE∽△DFA,∴ABF=AED.
中小学教育资源及组卷应用平台
15.(1)∵Rt△AB'C'是由 Rt△ABC绕点 A 按顺时针方向旋转得到的,∴ AC= AC',AB = AB',∠CAB =∠C'AB'.
,即∠CAC'=∠BAB'.
∵∠AEC=∠FEB,∴△ACE∽△FBE.
(2)当β=2α时,△ACE≌△FBE.
即
∴∠BCE=α.
∵∠ABC=α,∴∠ABC=∠BCE.∴CE=BE.
∵△ACE∽△FBE,
∴∠BEF=∠CEA,∠FBE=∠ACE.
∵CE=BE,∴△ACE≌△FBE.
同课章节目录
