4.3 相似三角形提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.3 相似三角形提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 262.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:36:36 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.3 相似三角形
基础巩固
1.如图所示,若△ABC∽△DEF,则∠E 的度数为( ).
A.28° B.32° C.42° D.52°
2.如果一个直角三角形的两条边长分别是6 和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值为( ).
A. B.5 C. 或5 D.无数个
3.如图所示,在△ABC中,点 D 在线段BC 上,且△ABC∽△DBA,则下列结论中,一定正确的是( ).
B
C. AB·AD=BD·BC D. AB·AD=AD·CD
4.已知△ABC的三边长是 , ,2,△DEF 的两边长分别是1 和 ,如果△ABC 与△DEF 相似,那么△DEF 的第三边长应该是 .
5.如图所示,在△ABC中,AB=8,AC=6,D是线段AC 的中点,点E 在线段AB 上,且△ADE∽△ABC,则AE的长为 .
6.如图所示,AD=2,AC=4,BC=6,∠B=36°,∠D=107°,△ABC∽△DAC.求:
(1)AB的长.
(2)CD的长.
(3)∠BAD的大小.
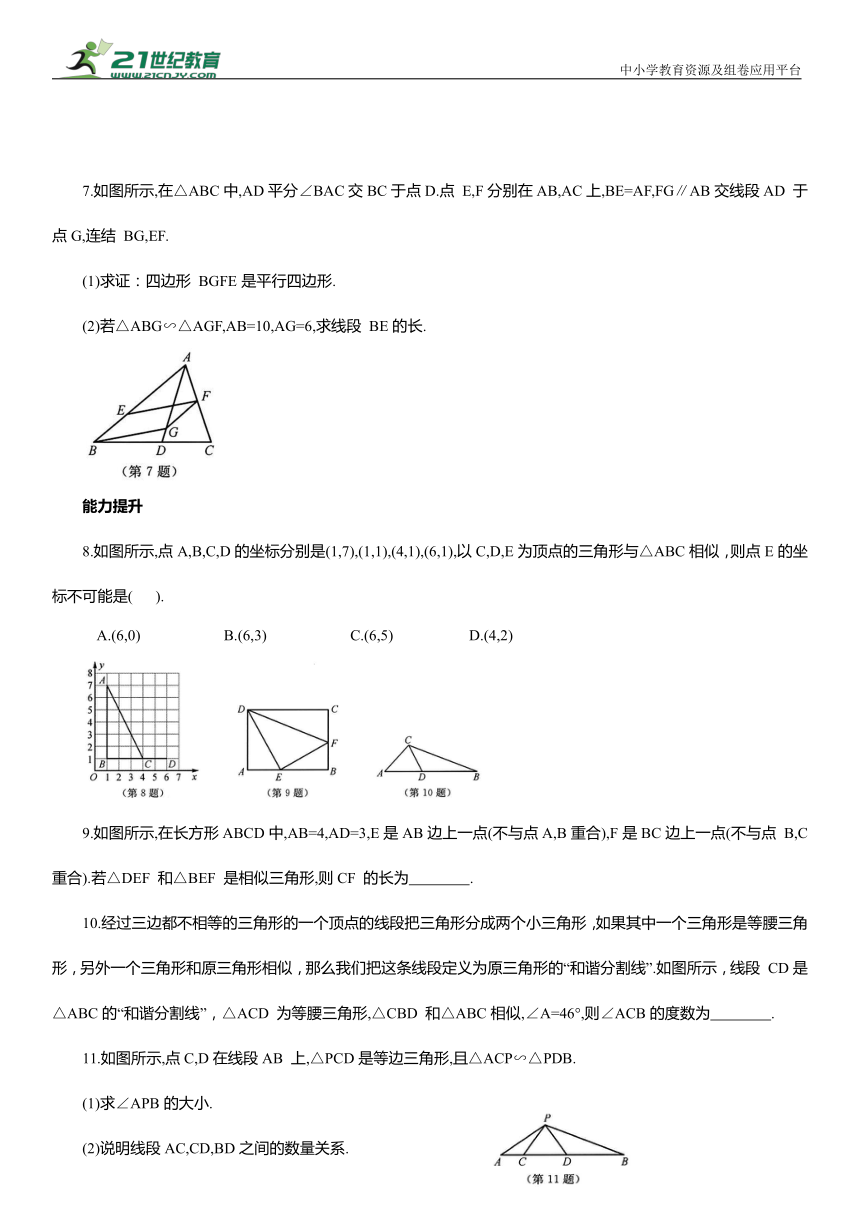
7.如图所示,在△ABC中,AD平分∠BAC交BC于点D.点 E,F分别在AB,AC上,BE=AF,FG∥AB交线段AD 于点G,连结 BG,EF.
(1)求证:四边形 BGFE是平行四边形.
(2)若△ABG∽△AGF,AB=10,AG=6,求线段 BE的长.
能力提升
8.如图所示,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ).
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
9.如图所示,在长方形ABCD中,AB=4,AD=3,E是AB边上一点(不与点A,B重合),F是BC边上一点(不与点 B,C重合).若△DEF 和△BEF 是相似三角形,则CF 的长为 .
10.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形相似,那么我们把这条线段定义为原三角形的“和谐分割线”.如图所示,线段 CD是△ABC的“和谐分割线”,△ACD 为等腰三角形,△CBD 和△ABC相似,∠A=46°,则∠ACB的度数为 .
11.如图所示,点C,D在线段AB 上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC,CD,BD之间的数量关系.
12.如图所示,已知,在平面直角坐标系中有四点:A(-2,4),B(-2,0),C(2,-3),D(2,0),设P是x轴上的点,且PA,PB,AB所围成的三角形与 PC,PD,CD 所围成的三角形相似,请求出所有符合上述条件的点 P 的坐标.
夯实演练
13.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为( ).
或 B.15
14.如图所示,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点 P 沿直线剪下一个与△ABC 相似的小三角形纸板,如果有4种不同的剪法,那么 AP 长的取值范围是 .
15.如图所示,已知△ABC∽△A B C ,相似比为k(k>1),且△ABC的三边长分别为a,b,c(a>b>c),△A B C 的三边长分别为a1,b2,c3.
(1)若c=a1,求证:a= kc.
(2)若c=a2,试给出两组正整数a,b,c和a1,b1,c1使得△ABC和△A B C 相似,并加以说明.
(3)若b=a1,c=b1,是否存在△ABC和△A B C 使得k=2 请说明理由.
4.2 由平行线截得的比例线段
1. C 2. D 3. B 4. 5. 6.
7.∵四边形 ABCD是矩形,AD=2,CD=1,
∴BC=AD=2,AB=CD=1,∠ABC=∠C=90°,AB∥DC.∴EB=AB=1.
在Rt△ABE中,
在 Rt△DCE中,
8.∵AD是△ABC的角平分线,∴∠BAD=∠CAD.
∵AD∥CE,∴∠BAD=∠E,∠CAD=∠ACE.
∴∠E=∠ACE.∴AC=AE.
9. A 10. B 11.2n+1
12.(1)∵EF∥BD,∴CD=BD.
∵四边形ABCD是平行四边形,∴AB=CD.
∴GH=6.
13. B 14.4
15.(1)如答图所示,过点 D 作DE∥BP交AP 于点 E.
∵D是AB的中点,
∴E为AP中点.
∵PPC=2,∴AE=PE=PC.
∴PQ是△CDE 的中位线,DE 是△ABP 的中位线.
∴BP=2DE=4PQ.
(2)BP=(m+2)PQ.
证明:如答图所示,过点 D作 DE∥BP交AP 于点E.
∵D是AB中点,∴E是AP中点.
∴BP=2DE,AP=2PE.
∴BP=2DE=(m+2)PQ.
4.3 相似三角形
基础巩固
1.如图所示,若△ABC∽△DEF,则∠E 的度数为( ).
A.28° B.32° C.42° D.52°
2.如果一个直角三角形的两条边长分别是6 和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值为( ).
A. B.5 C. 或5 D.无数个
3.如图所示,在△ABC中,点 D 在线段BC 上,且△ABC∽△DBA,则下列结论中,一定正确的是( ).
B
C. AB·AD=BD·BC D. AB·AD=AD·CD
4.已知△ABC的三边长是 , ,2,△DEF 的两边长分别是1 和 ,如果△ABC 与△DEF 相似,那么△DEF 的第三边长应该是 .
5.如图所示,在△ABC中,AB=8,AC=6,D是线段AC 的中点,点E 在线段AB 上,且△ADE∽△ABC,则AE的长为 .
6.如图所示,AD=2,AC=4,BC=6,∠B=36°,∠D=107°,△ABC∽△DAC.求:
(1)AB的长.
(2)CD的长.
(3)∠BAD的大小.
7.如图所示,在△ABC中,AD平分∠BAC交BC于点D.点 E,F分别在AB,AC上,BE=AF,FG∥AB交线段AD 于点G,连结 BG,EF.
(1)求证:四边形 BGFE是平行四边形.
(2)若△ABG∽△AGF,AB=10,AG=6,求线段 BE的长.
能力提升
8.如图所示,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( ).
A.(6,0) B.(6,3) C.(6,5) D.(4,2)
9.如图所示,在长方形ABCD中,AB=4,AD=3,E是AB边上一点(不与点A,B重合),F是BC边上一点(不与点 B,C重合).若△DEF 和△BEF 是相似三角形,则CF 的长为 .
10.经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个三角形是等腰三角形,另外一个三角形和原三角形相似,那么我们把这条线段定义为原三角形的“和谐分割线”.如图所示,线段 CD是△ABC的“和谐分割线”,△ACD 为等腰三角形,△CBD 和△ABC相似,∠A=46°,则∠ACB的度数为 .
11.如图所示,点C,D在线段AB 上,△PCD是等边三角形,且△ACP∽△PDB.
(1)求∠APB的大小.
(2)说明线段AC,CD,BD之间的数量关系.
12.如图所示,已知,在平面直角坐标系中有四点:A(-2,4),B(-2,0),C(2,-3),D(2,0),设P是x轴上的点,且PA,PB,AB所围成的三角形与 PC,PD,CD 所围成的三角形相似,请求出所有符合上述条件的点 P 的坐标.
夯实演练
13.已知两个直角三角形的三边长分别为3,4,m和6,8,n,且这两个直角三角形不相似,则m+n的值为( ).
或 B.15
14.如图所示,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点 P 沿直线剪下一个与△ABC 相似的小三角形纸板,如果有4种不同的剪法,那么 AP 长的取值范围是 .
15.如图所示,已知△ABC∽△A B C ,相似比为k(k>1),且△ABC的三边长分别为a,b,c(a>b>c),△A B C 的三边长分别为a1,b2,c3.
(1)若c=a1,求证:a= kc.
(2)若c=a2,试给出两组正整数a,b,c和a1,b1,c1使得△ABC和△A B C 相似,并加以说明.
(3)若b=a1,c=b1,是否存在△ABC和△A B C 使得k=2 请说明理由.
4.2 由平行线截得的比例线段
1. C 2. D 3. B 4. 5. 6.
7.∵四边形 ABCD是矩形,AD=2,CD=1,
∴BC=AD=2,AB=CD=1,∠ABC=∠C=90°,AB∥DC.∴EB=AB=1.
在Rt△ABE中,
在 Rt△DCE中,
8.∵AD是△ABC的角平分线,∴∠BAD=∠CAD.
∵AD∥CE,∴∠BAD=∠E,∠CAD=∠ACE.
∴∠E=∠ACE.∴AC=AE.
9. A 10. B 11.2n+1
12.(1)∵EF∥BD,∴CD=BD.
∵四边形ABCD是平行四边形,∴AB=CD.
∴GH=6.
13. B 14.4
15.(1)如答图所示,过点 D 作DE∥BP交AP 于点 E.
∵D是AB的中点,
∴E为AP中点.
∵PPC=2,∴AE=PE=PC.
∴PQ是△CDE 的中位线,DE 是△ABP 的中位线.
∴BP=2DE=4PQ.
(2)BP=(m+2)PQ.
证明:如答图所示,过点 D作 DE∥BP交AP 于点E.
∵D是AB中点,∴E是AP中点.
∴BP=2DE,AP=2PE.
∴BP=2DE=(m+2)PQ.
同课章节目录
