4.6 相似多边形 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.6 相似多边形 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 302.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-01 17:35:52 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.6 相似多边形
基础巩固
1.在矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD 相似的为( ).
2.下列说法中,错误的是( ).
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3.如图所示的图形都可以看作某种特殊的“细胞”,它们分裂时能同时分裂为全等的4个小细胞,分裂的小细胞与原图形相似,则相似比为( ).
A.1:4 B.1:3 C.1:2
4.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使点B 落在AD 上的点F 处,若四边形 EFDC与矩形ABCD 相似,则AD的长为( ).
C. D.2
5.如图所示,在周长为9cm的四边形ABCD中,AC⊥BD于点O,且AC=BD=3cm,顺次连结OA,OB,OC,OD得中点得四边形A1B1C1D1,顺次连结OA1,OB1,OC1,OD1的中点得四边形 A2B2C2D2……依此作下去,得四边形 AnBnCnDn.四边形AnBnCnDn的周长为 (用含n的代数式表示,下同) cm,面积为 cm .
6.如图所示,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E 和F(点E在点 F 的左侧),若要使四边形 DEBF 与菱形ABCD 相似,则AE的长为 .
7.如图所示,E是菱形ABCD 对角线CA 的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形 AEFG∽菱形 ABCD,连结 EB,GD.
(1)求证:EB=GD.
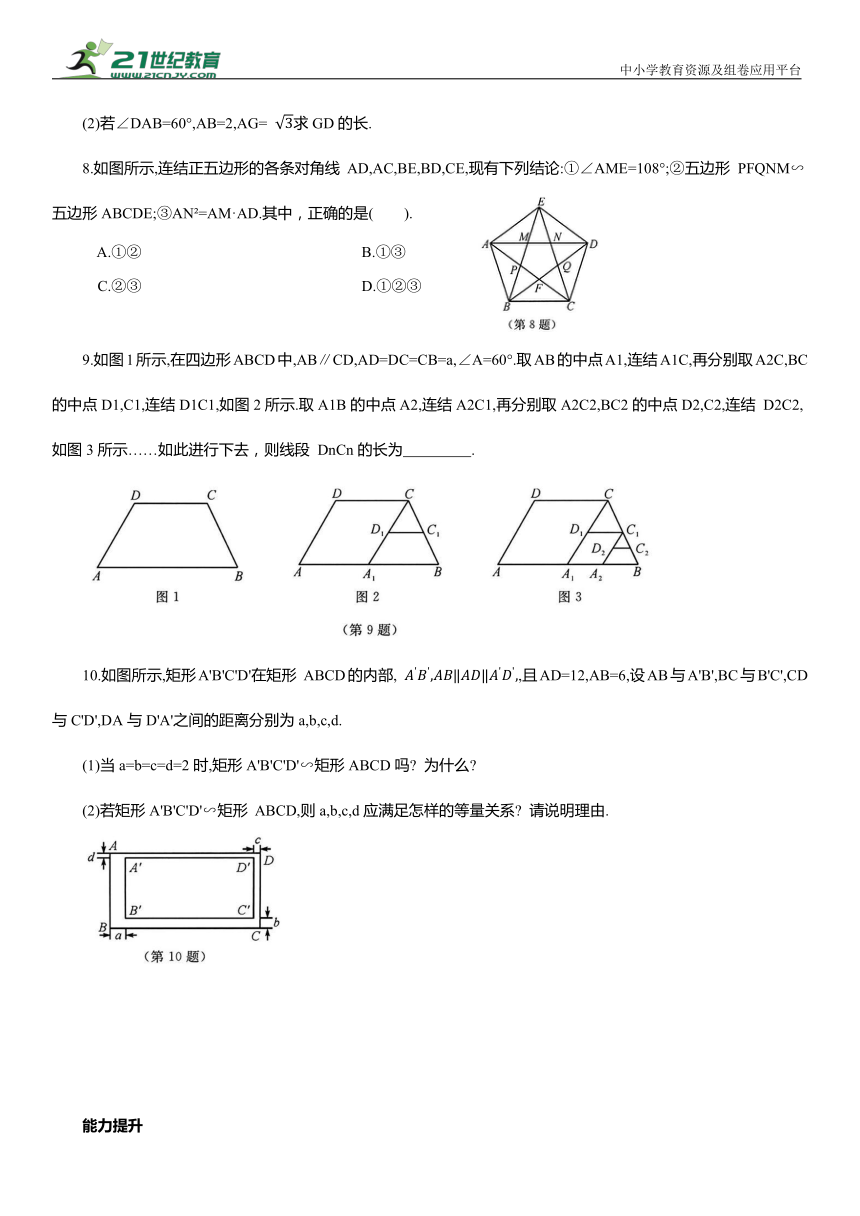
(2)若∠DAB=60°,AB=2,AG= 求GD的长.
8.如图所示,连结正五边形的各条对角线 AD,AC,BE,BD,CE,现有下列结论:①∠AME=108°;②五边形 PFQNM∽五边形ABCDE;③AN =AM·AD.其中,正确的是( ).
A.①② B.①③
C.②③ D.①②③
9.如图1所示,在四边形ABCD中,AB∥CD,AD=DC=CB=a,∠A=60°.取AB的中点A1,连结A1C,再分别取A2C,BC的中点D1,C1,连结D1C1,如图2所示.取A1B的中点A2,连结A2C1,再分别取A2C2,BC2的中点D2,C2,连结 D2C2,如图3所示……如此进行下去,则线段 DnCn的长为 .
10.如图所示,矩形A'B'C'D'在矩形 ABCD的内部, ,且AD=12,AB=6,设AB与A'B',BC与B'C',CD与C'D',DA与D'A'之间的距离分别为a,b,c,d.
(1)当a=b=c=d=2时,矩形A'B'C'D'∽矩形ABCD吗 为什么
(2)若矩形A'B'C'D'∽矩形 ABCD,则a,b,c,d应满足怎样的等量关系 请说明理由.
能力提升
11.如图所示,在矩形ABCD中,AD=2,CD=1,连结AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连结AC1,以对角线 为边作矩形. 的相似矩形AB2C2C1……按此规律继续下去,则矩形. 的面积为 .
12.已知菱形A1B1C1D1 的边长为2, ,对角线. 相交于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的平面直角坐标系,以B1D1 为对角线作菱形 B1C2D1A2∽菱形 A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形 B1C2D1A2再以 B2D2为对角线作菱形 菱形A2B2C2D2……按此规律继续作下去,在x轴的正半轴上得到点. 则点 An的坐标为 .
13.数学学习小组在学过相似图形的知识后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.例如:我们可以定义:长和宽之比相等的矩形是相似矩形;相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长之比等于相似比,面积之比等于相似比的平方等.请你参与这个学习小组,一同探索这类问题.
(1)写出判定菱形相似的一种判定方法.
(2)如图所示,将菱形ABCD沿着直线AC 向右平移后得到菱形A'B'C'D',试证明:四边形 A'FCE 是菱形,且菱形ABCD∽菱形A'FCE.
(3)若. ,菱形A'FCE 的面积是菱形ABCD 面积的一半,求平移的距离AA'的长.
4.6 相似多边形
7.(1)∵菱形 AEFG∽菱形 ABCD,∴∠EAG=∠BAD.
∴∠EAG+∠GAD+∠GAB=∠BAB.
∴∠EAB=∠GAD.
∵AE=AG,AB=AD,∴△AEB≌△AGD.∴EB=GD.
(2)如答图所示,连结 BD交AC 于点 P,则 BP⊥AC.
∵∠DAB=60°,∴∠PAB=30°.
8. D 9. a
10.(1)不相似.
理由如下: ∴矩形 A'B'C'D'与矩形ABCD 不相似.
(2)要使矩形 A'B'C'D'∽矩形 ABCD,就要 即 可得a+c=2b+2d.
∴当a+c=2b+2d时,矩形A'B'C'D'∽矩形 ABCD.
13.(1)若两个菱形有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似.
(2)∵AD∥A'E∥FC,AB∥A'F∥EC,
∴四边形 A'FCE 为平行四边形,△CEA'∽△CDA,
∵AD=AB,∴EA'=FA'.∴四边形 A'FCE 为菱形.
∵∠EA'F=∠DAB,∴菱形A'FCE∽菱形ABCD.
(3)∵菱形 ABCD∽菱形 A'FCE,菱形 A'FCE 的面积是菱形ABCD 面积的一半,
∴菱形ABCD与菱形A'FCE 的面积比为2:1.
∴对应边之比为 :1,即
4.6 相似多边形
基础巩固
1.在矩形ABCD中,AB=4,BC=3,下列四个矩形中,与矩形ABCD 相似的为( ).
2.下列说法中,错误的是( ).
A.等边三角形都相似 B.等腰直角三角形都相似
C.矩形都相似 D.正方形都相似
3.如图所示的图形都可以看作某种特殊的“细胞”,它们分裂时能同时分裂为全等的4个小细胞,分裂的小细胞与原图形相似,则相似比为( ).
A.1:4 B.1:3 C.1:2
4.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使点B 落在AD 上的点F 处,若四边形 EFDC与矩形ABCD 相似,则AD的长为( ).
C. D.2
5.如图所示,在周长为9cm的四边形ABCD中,AC⊥BD于点O,且AC=BD=3cm,顺次连结OA,OB,OC,OD得中点得四边形A1B1C1D1,顺次连结OA1,OB1,OC1,OD1的中点得四边形 A2B2C2D2……依此作下去,得四边形 AnBnCnDn.四边形AnBnCnDn的周长为 (用含n的代数式表示,下同) cm,面积为 cm .
6.如图所示,菱形ABCD的周长为12,∠DAB=60°,对角线AC上有两点E 和F(点E在点 F 的左侧),若要使四边形 DEBF 与菱形ABCD 相似,则AE的长为 .
7.如图所示,E是菱形ABCD 对角线CA 的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形 AEFG∽菱形 ABCD,连结 EB,GD.
(1)求证:EB=GD.
(2)若∠DAB=60°,AB=2,AG= 求GD的长.
8.如图所示,连结正五边形的各条对角线 AD,AC,BE,BD,CE,现有下列结论:①∠AME=108°;②五边形 PFQNM∽五边形ABCDE;③AN =AM·AD.其中,正确的是( ).
A.①② B.①③
C.②③ D.①②③
9.如图1所示,在四边形ABCD中,AB∥CD,AD=DC=CB=a,∠A=60°.取AB的中点A1,连结A1C,再分别取A2C,BC的中点D1,C1,连结D1C1,如图2所示.取A1B的中点A2,连结A2C1,再分别取A2C2,BC2的中点D2,C2,连结 D2C2,如图3所示……如此进行下去,则线段 DnCn的长为 .
10.如图所示,矩形A'B'C'D'在矩形 ABCD的内部, ,且AD=12,AB=6,设AB与A'B',BC与B'C',CD与C'D',DA与D'A'之间的距离分别为a,b,c,d.
(1)当a=b=c=d=2时,矩形A'B'C'D'∽矩形ABCD吗 为什么
(2)若矩形A'B'C'D'∽矩形 ABCD,则a,b,c,d应满足怎样的等量关系 请说明理由.
能力提升
11.如图所示,在矩形ABCD中,AD=2,CD=1,连结AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连结AC1,以对角线 为边作矩形. 的相似矩形AB2C2C1……按此规律继续下去,则矩形. 的面积为 .
12.已知菱形A1B1C1D1 的边长为2, ,对角线. 相交于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的平面直角坐标系,以B1D1 为对角线作菱形 B1C2D1A2∽菱形 A1B1C1D1,再以A2C2为对角线作菱形A2B2C2D2∽菱形 B1C2D1A2再以 B2D2为对角线作菱形 菱形A2B2C2D2……按此规律继续作下去,在x轴的正半轴上得到点. 则点 An的坐标为 .
13.数学学习小组在学过相似图形的知识后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.例如:我们可以定义:长和宽之比相等的矩形是相似矩形;相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长之比等于相似比,面积之比等于相似比的平方等.请你参与这个学习小组,一同探索这类问题.
(1)写出判定菱形相似的一种判定方法.
(2)如图所示,将菱形ABCD沿着直线AC 向右平移后得到菱形A'B'C'D',试证明:四边形 A'FCE 是菱形,且菱形ABCD∽菱形A'FCE.
(3)若. ,菱形A'FCE 的面积是菱形ABCD 面积的一半,求平移的距离AA'的长.
4.6 相似多边形
7.(1)∵菱形 AEFG∽菱形 ABCD,∴∠EAG=∠BAD.
∴∠EAG+∠GAD+∠GAB=∠BAB.
∴∠EAB=∠GAD.
∵AE=AG,AB=AD,∴△AEB≌△AGD.∴EB=GD.
(2)如答图所示,连结 BD交AC 于点 P,则 BP⊥AC.
∵∠DAB=60°,∴∠PAB=30°.
8. D 9. a
10.(1)不相似.
理由如下: ∴矩形 A'B'C'D'与矩形ABCD 不相似.
(2)要使矩形 A'B'C'D'∽矩形 ABCD,就要 即 可得a+c=2b+2d.
∴当a+c=2b+2d时,矩形A'B'C'D'∽矩形 ABCD.
13.(1)若两个菱形有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似.
(2)∵AD∥A'E∥FC,AB∥A'F∥EC,
∴四边形 A'FCE 为平行四边形,△CEA'∽△CDA,
∵AD=AB,∴EA'=FA'.∴四边形 A'FCE 为菱形.
∵∠EA'F=∠DAB,∴菱形A'FCE∽菱形ABCD.
(3)∵菱形 ABCD∽菱形 A'FCE,菱形 A'FCE 的面积是菱形ABCD 面积的一半,
∴菱形ABCD与菱形A'FCE 的面积比为2:1.
∴对应边之比为 :1,即
同课章节目录
