4.1 比例线段(1) 提优训练(含答案)2024-2025学年浙教版九年级数学上册
文档属性
| 名称 | 4.1 比例线段(1) 提优训练(含答案)2024-2025学年浙教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 190.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-06 19:03:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
4.1 比例线段(1)
基础巩固
1.若C是线段AB上的一点,且AC:CB=2:3,则AB:BC为( ).
A.2:3 B.5:3 C.3:2 D.3:5
2.在比例尺为1:10000000 的地图上,量得甲、乙两地的距离是30cm,则两地的实际距离为( ).
A.30km B.300km C.3000km D.30000km
3.若以下列各组长度(同一单位)为长取四条线段,则不成比例的一组是( ).
A.2,5,10,25 B.4,7,4,7 C.2, , ,4
4.鄂尔多斯市成陵旅游区到响沙湾旅游区之间的距离为105km,那么在一张比例尺为1:2000000的交通旅游图上,它们之间的距离大约相当于( ).
A.一根火柴的长度 B.一支钢笔的长度 C.一支铅笔的长度 D.一根筷子的长度
5.若线段 则线段a,b,c 的第四比例项是 cm.
6.如果C是线段AB上一点,BC=2AC,M,N分别是线段AC,BC的中点,那么MN: BC = .
7.如图所示,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.找出图中的一组比例线段,并说明理由.
8.如图所示,在△ABC中,∠B=30°,∠C=45°.
(1)求 的值.
(2)求 AB:AC:BC.
能力提升
9.已知甲、乙两幅地图的比例尺分别为1:5000和1:20000,如果甲图上A,B两地的距离与乙图上C,D两地的距离恰好相等,那么A,B两地的实际距离与C,D两地的实际距离之比为( ).
A.5:2 B.2:5 C.1:4 D.4:1
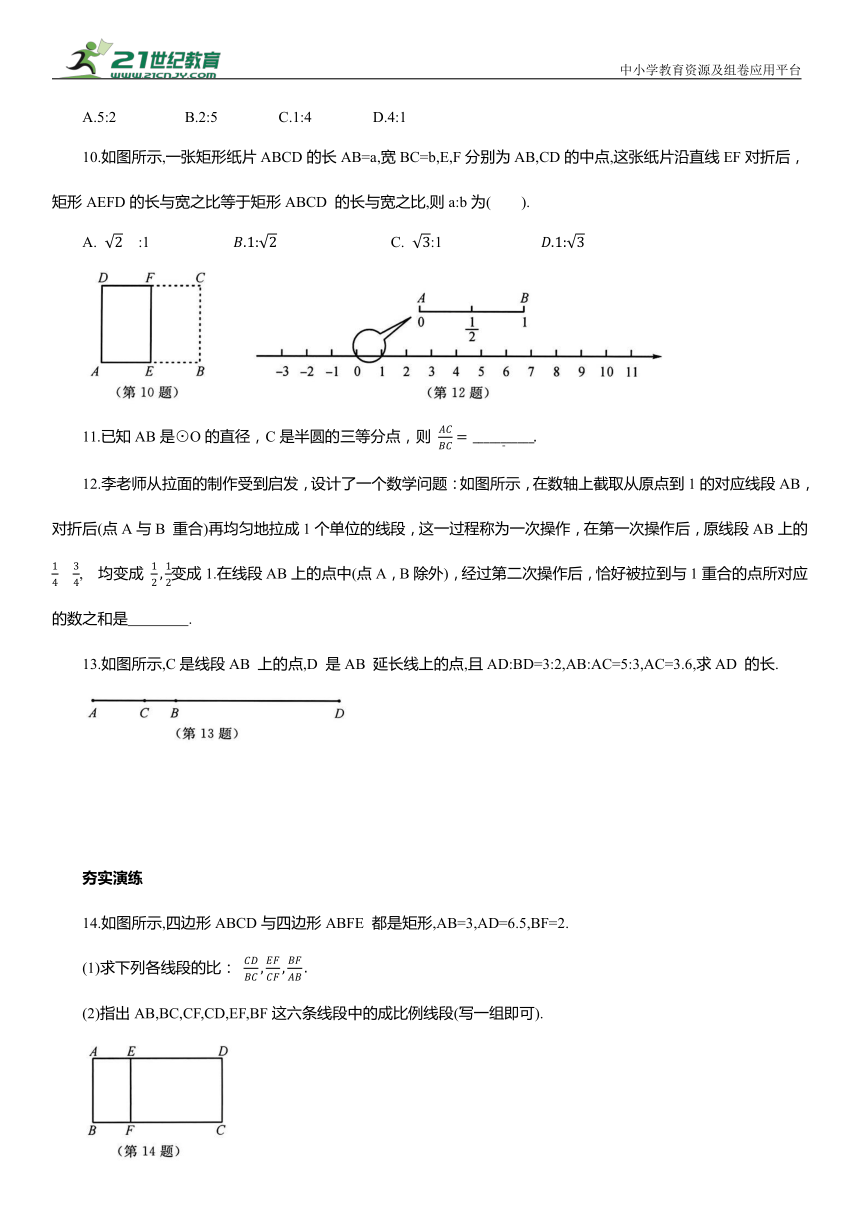
10.如图所示,一张矩形纸片ABCD的长AB=a,宽BC=b,E,F分别为AB,CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD 的长与宽之比,则a:b为( ).
A. :1 C. :1
11.已知AB是⊙O的直径,C是半圆的三等分点,则
12.李老师从拉面的制作受到启发,设计了一个数学问题:如图所示,在数轴上截取从原点到1的对应线段AB,对折后(点A与B 重合)再均匀地拉成1个单位的线段,这一过程称为一次操作,在第一次操作后,原线段AB上的 , 均变成 变成1.在线段AB上的点中(点A,B除外),经过第二次操作后,恰好被拉到与1重合的点所对应的数之和是 .
13.如图所示,C是线段AB 上的点,D 是AB 延长线上的点,且AD:BD=3:2,AB:AC=5:3,AC=3.6,求AD 的长.
夯实演练
14.如图所示,四边形ABCD与四边形ABFE 都是矩形,AB=3,AD=6.5,BF=2.
(1)求下列各线段的比:
(2)指出AB,BC,CF,CD,EF,BF这六条线段中的成比例线段(写一组即可).
15.若在比例尺为 1 :6700000 的地图上量得我国国土南北的最大距离是82.09cm,则实际上这一距离大约是 km(结果精确到1km).
16.已知点 P 在线段AB上,且AP:BP=2:3,则AB:PB为 .
17.在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)如果三条线段a,b,c满足a:b=b:c=k,这三条线段能否构成三角形 如果能,请指出三角形的形状;如果不能,请说明理由.
1. B 2. D 3. C 4. D 5.1:3 6.2:5 7.23
8.(1)由a:b=c:x得
(2)由b:y=y:c得 ∴y=±1.
9. B 10. A 11. 12.
13.设 则a=3k,b=4k,c=5k.
∵a+b+c=36,∴3k+4k+5k=36,解得k=3.
∴a=3k=9,b=4k=12,c=5k=15.
∴△ABC三边的长为a=9,b=12,c=15.
14.设 则a=3k-2,b=4k,c=6k
∴2(3k-2)-4k+3(6k-5)=21,解得k=2.
∴a=4,b=8,c=7.
∴a:b:c=4:8:7.
15. A 16.
17.设比值为k,则:2a-b-c= ka,-a-c+2b= kb,-a-b+2c= kc,
∴b+c=(2-k)a,a+c=(2-k)b,a+b=(2-k)c.
4.1 比例线段(1)
基础巩固
1.若C是线段AB上的一点,且AC:CB=2:3,则AB:BC为( ).
A.2:3 B.5:3 C.3:2 D.3:5
2.在比例尺为1:10000000 的地图上,量得甲、乙两地的距离是30cm,则两地的实际距离为( ).
A.30km B.300km C.3000km D.30000km
3.若以下列各组长度(同一单位)为长取四条线段,则不成比例的一组是( ).
A.2,5,10,25 B.4,7,4,7 C.2, , ,4
4.鄂尔多斯市成陵旅游区到响沙湾旅游区之间的距离为105km,那么在一张比例尺为1:2000000的交通旅游图上,它们之间的距离大约相当于( ).
A.一根火柴的长度 B.一支钢笔的长度 C.一支铅笔的长度 D.一根筷子的长度
5.若线段 则线段a,b,c 的第四比例项是 cm.
6.如果C是线段AB上一点,BC=2AC,M,N分别是线段AC,BC的中点,那么MN: BC = .
7.如图所示,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.找出图中的一组比例线段,并说明理由.
8.如图所示,在△ABC中,∠B=30°,∠C=45°.
(1)求 的值.
(2)求 AB:AC:BC.
能力提升
9.已知甲、乙两幅地图的比例尺分别为1:5000和1:20000,如果甲图上A,B两地的距离与乙图上C,D两地的距离恰好相等,那么A,B两地的实际距离与C,D两地的实际距离之比为( ).
A.5:2 B.2:5 C.1:4 D.4:1
10.如图所示,一张矩形纸片ABCD的长AB=a,宽BC=b,E,F分别为AB,CD的中点,这张纸片沿直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD 的长与宽之比,则a:b为( ).
A. :1 C. :1
11.已知AB是⊙O的直径,C是半圆的三等分点,则
12.李老师从拉面的制作受到启发,设计了一个数学问题:如图所示,在数轴上截取从原点到1的对应线段AB,对折后(点A与B 重合)再均匀地拉成1个单位的线段,这一过程称为一次操作,在第一次操作后,原线段AB上的 , 均变成 变成1.在线段AB上的点中(点A,B除外),经过第二次操作后,恰好被拉到与1重合的点所对应的数之和是 .
13.如图所示,C是线段AB 上的点,D 是AB 延长线上的点,且AD:BD=3:2,AB:AC=5:3,AC=3.6,求AD 的长.
夯实演练
14.如图所示,四边形ABCD与四边形ABFE 都是矩形,AB=3,AD=6.5,BF=2.
(1)求下列各线段的比:
(2)指出AB,BC,CF,CD,EF,BF这六条线段中的成比例线段(写一组即可).
15.若在比例尺为 1 :6700000 的地图上量得我国国土南北的最大距离是82.09cm,则实际上这一距离大约是 km(结果精确到1km).
16.已知点 P 在线段AB上,且AP:BP=2:3,则AB:PB为 .
17.在线段AB上存在一点C,满足AC:CB=CB:AB=k.
(1)求k的值.
(2)如果三条线段a,b,c满足a:b=b:c=k,这三条线段能否构成三角形 如果能,请指出三角形的形状;如果不能,请说明理由.
1. B 2. D 3. C 4. D 5.1:3 6.2:5 7.23
8.(1)由a:b=c:x得
(2)由b:y=y:c得 ∴y=±1.
9. B 10. A 11. 12.
13.设 则a=3k,b=4k,c=5k.
∵a+b+c=36,∴3k+4k+5k=36,解得k=3.
∴a=3k=9,b=4k=12,c=5k=15.
∴△ABC三边的长为a=9,b=12,c=15.
14.设 则a=3k-2,b=4k,c=6k
∴2(3k-2)-4k+3(6k-5)=21,解得k=2.
∴a=4,b=8,c=7.
∴a:b:c=4:8:7.
15. A 16.
17.设比值为k,则:2a-b-c= ka,-a-c+2b= kb,-a-b+2c= kc,
∴b+c=(2-k)a,a+c=(2-k)b,a+b=(2-k)c.
同课章节目录
