1.1 锐角三角函数(1)课件
图片预览





文档简介
(共23张PPT)
(浙教版版)九年级
下
1.1 锐角三角函数(1)
解直角三角形
第一章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
作业布置
06
目录
内容总览
教学目标
1. 经历锐角三角函数概念的探究过程,构建获得锐角三角
函数定义的方法;
2. 理解锐角三角函数的概念;
3. 会在直角三角形中求锐角的正弦值、余弦值和正切值.
新知导入
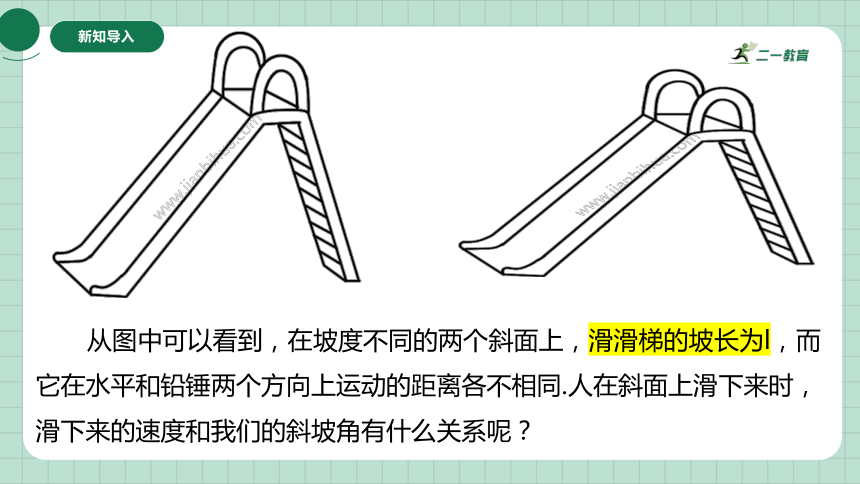
从图中可以看到,在坡度不同的两个斜面上,滑滑梯的坡长为l,而它在水平和铅锤两个方向上运动的距离各不相同.人在斜面上滑下来时,滑下来的速度和我们的斜坡角有什么关系呢?
新知导入
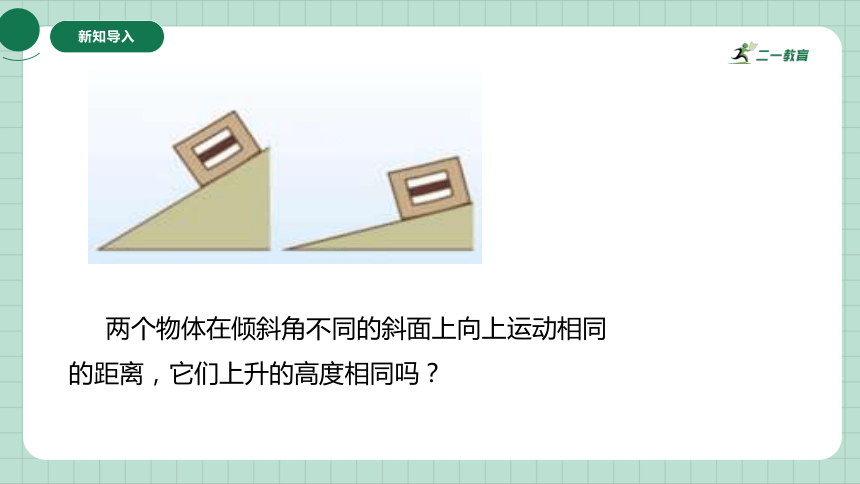
两个物体在倾斜角不同的斜面上向上运动相同
的距离,它们上升的高度相同吗?
从下图我们可以看到,在倾斜角(∠α ,∠ β)不同的两个斜面上,物体前进的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同。物体在斜面上运动时,在斜面上所经
过的距离和水平方向、铅垂方向经过的距离,
与斜面的倾斜角之间有什么关系呢?
越陡—倾斜角___
新知导入
越大
实验操作
与点B 在角的边上的位置无关.
1.作一个30°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
用刻度尺量取直角三角形的三边,计算 的值,并将所得的结果与你的同伴所得的结果作比较,你发现了什么?.
结论:当∠A=30°时,
比值 是一个确定的值
实验操作
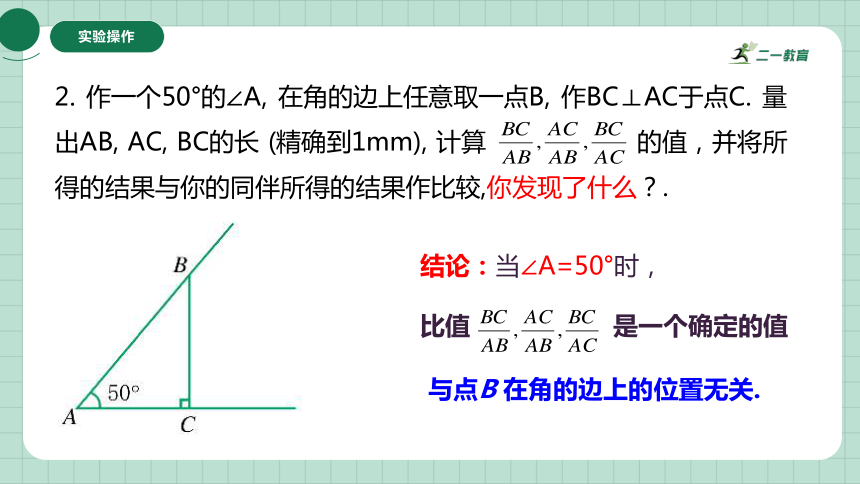
2. 作一个50°的∠A, 在角的边上任意取一点B, 作BC⊥AC于点C. 量出AB, AC, BC的长 (精确到1mm), 计算 的值,并将所得的结果与你的同伴所得的结果作比较,你发现了什么?.
与点B 在角的边上的位置无关.
结论:当∠A=50°时,
比值 是一个确定的值
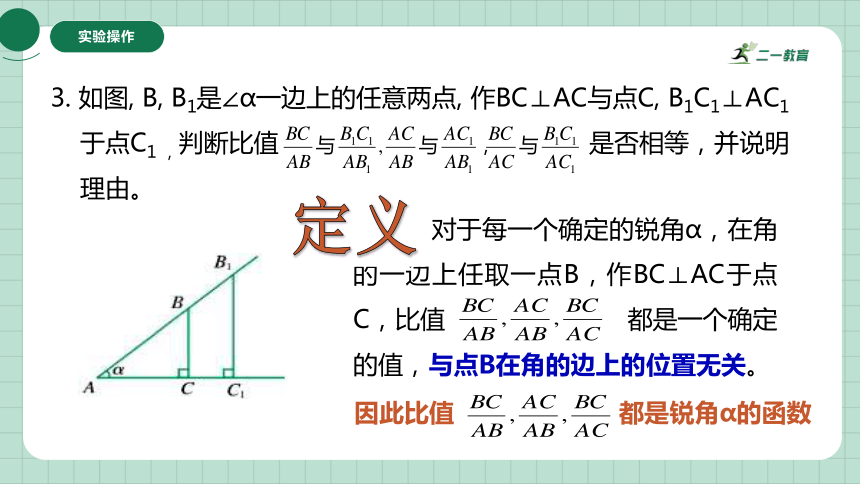
3. 如图, B, B1是∠α一边上的任意两点, 作BC⊥AC与点C, B1C1⊥AC1
于点C1 ,判断比值 是否相等,并说明
理由。
实验操作
相等. 对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,比值 都是一个确定的值,与点B在角的边上的位置无关。
定义
因此比值 都是锐角α的函数
新知讲解
C
B
A
∠A的对边
∠A的邻边
斜边
sin A=
=
∠A的正弦
∠A的余弦
=
cos A=
∠A的正切
tan A=
=
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
新知讲解
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、sinA 是一个比值 4、sinA 没有单位
C
B
A
∠A的对边
∠A的邻边
斜边
注意
事项
典例精析
A
B
C
例1:如图, 在Rt△ABC中,∠C=90°,AB=5,BC=3,
求∠A、∠B的正弦、余弦和正切.
5
3
4
课堂练习
1. 如图, ∠ACB=90°,CD⊥AB.
在上图中,若BD=6,CD=12. 求 cos A 的值.
┍
┌
A
C
B
D
AC
AB
BC
CD
AD
AC
6
12
课堂练习
若BD=6,CD=12. 求 cosA 的值.
┍
┌
A
C
B
D
6
12
课堂总结
求锐角的三角函数值的三种方法:
1.在直角三角形里,确定各个边,根据定义直接求出.
2.利用相似、全等等关系,寻找与所求角相等的角
(若该角的三角函数值知道或者易求).
3.利用互余的两个角间的特殊关系求.
4. 求锐角三角函数时,勾股定理的运用是很重要的.
课堂练习
1、在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )
A、4tan50° B、4tan40° C、4sin50° D、4sin40°
B
2. 如图,∠α 的顶点为O,它的一边在x 轴的
正半轴上,另一边OA上有一点P (b,4),
若sin α= ,则b=______ .
3
3、如图,将△ABC 放在每个小正方形的边长为1的网格中,
点A,B,C均在格点上,则 tanA 的值是( )
A、 B、 C、 2 D、
D
4. 在Rt△ABC 中,∠C=90°,AB︰BC=1︰2,
tanB=________,sinB=________,cosB=__________.
综合拓展
板书设计
C
B
A
∠A的
对边
∠A的邻边
斜边
sin A=
=
∠A的正弦
∠A的余弦
=
cos A=
∠A的正切
tan A=
=
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
作业布置
1.如图△ABC中∠C=90°,BC=5, AC=12.
判断:(1)sinA= ( )
(2)tanB= ( )
√
×
A
B
C
2. 如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B. 缩小100倍
C.不变 D. 不能确定
C
3. 在Rt△ABC中,∠C为Rt∠ .
求证:sin2A+cos2A=1.
证明:∵∠C=Rt∠
∵ AC2+BC2=AB2
∴sinA= ,cosA=
作业布置
4. 如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3, BC=4,求sinα,cosα,tanα的值.
作业布置
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
(浙教版版)九年级
下
1.1 锐角三角函数(1)
解直角三角形
第一章
“—”
教学目标
01
新知导入
02
新知讲解
03
课堂练习
04
课堂总结
05
作业布置
06
目录
内容总览
教学目标
1. 经历锐角三角函数概念的探究过程,构建获得锐角三角
函数定义的方法;
2. 理解锐角三角函数的概念;
3. 会在直角三角形中求锐角的正弦值、余弦值和正切值.
新知导入
从图中可以看到,在坡度不同的两个斜面上,滑滑梯的坡长为l,而它在水平和铅锤两个方向上运动的距离各不相同.人在斜面上滑下来时,滑下来的速度和我们的斜坡角有什么关系呢?
新知导入
两个物体在倾斜角不同的斜面上向上运动相同
的距离,它们上升的高度相同吗?
从下图我们可以看到,在倾斜角(∠α ,∠ β)不同的两个斜面上,物体前进的距离都是l,而它在水平和铅垂两个方向上运动的距离却各不相同。物体在斜面上运动时,在斜面上所经
过的距离和水平方向、铅垂方向经过的距离,
与斜面的倾斜角之间有什么关系呢?
越陡—倾斜角___
新知导入
越大
实验操作
与点B 在角的边上的位置无关.
1.作一个30°的∠A,在角的边上任意取一点B,作BC⊥AC于点C.
用刻度尺量取直角三角形的三边,计算 的值,并将所得的结果与你的同伴所得的结果作比较,你发现了什么?.
结论:当∠A=30°时,
比值 是一个确定的值
实验操作
2. 作一个50°的∠A, 在角的边上任意取一点B, 作BC⊥AC于点C. 量出AB, AC, BC的长 (精确到1mm), 计算 的值,并将所得的结果与你的同伴所得的结果作比较,你发现了什么?.
与点B 在角的边上的位置无关.
结论:当∠A=50°时,
比值 是一个确定的值
3. 如图, B, B1是∠α一边上的任意两点, 作BC⊥AC与点C, B1C1⊥AC1
于点C1 ,判断比值 是否相等,并说明
理由。
实验操作
相等. 对于每一个确定的锐角α,在角的一边上任取一点B,作BC⊥AC于点C,比值 都是一个确定的值,与点B在角的边上的位置无关。
定义
因此比值 都是锐角α的函数
新知讲解
C
B
A
∠A的对边
∠A的邻边
斜边
sin A=
=
∠A的正弦
∠A的余弦
=
cos A=
∠A的正切
tan A=
=
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
新知讲解
1、sinA 不是一个角 2、sinA不是 sin与A的乘积
3、sinA 是一个比值 4、sinA 没有单位
C
B
A
∠A的对边
∠A的邻边
斜边
注意
事项
典例精析
A
B
C
例1:如图, 在Rt△ABC中,∠C=90°,AB=5,BC=3,
求∠A、∠B的正弦、余弦和正切.
5
3
4
课堂练习
1. 如图, ∠ACB=90°,CD⊥AB.
在上图中,若BD=6,CD=12. 求 cos A 的值.
┍
┌
A
C
B
D
AC
AB
BC
CD
AD
AC
6
12
课堂练习
若BD=6,CD=12. 求 cosA 的值.
┍
┌
A
C
B
D
6
12
课堂总结
求锐角的三角函数值的三种方法:
1.在直角三角形里,确定各个边,根据定义直接求出.
2.利用相似、全等等关系,寻找与所求角相等的角
(若该角的三角函数值知道或者易求).
3.利用互余的两个角间的特殊关系求.
4. 求锐角三角函数时,勾股定理的运用是很重要的.
课堂练习
1、在△ABC中,∠C=90°,∠A=50°,BC=4,则AC为( )
A、4tan50° B、4tan40° C、4sin50° D、4sin40°
B
2. 如图,∠α 的顶点为O,它的一边在x 轴的
正半轴上,另一边OA上有一点P (b,4),
若sin α= ,则b=______ .
3
3、如图,将△ABC 放在每个小正方形的边长为1的网格中,
点A,B,C均在格点上,则 tanA 的值是( )
A、 B、 C、 2 D、
D
4. 在Rt△ABC 中,∠C=90°,AB︰BC=1︰2,
tanB=________,sinB=________,cosB=__________.
综合拓展
板书设计
C
B
A
∠A的
对边
∠A的邻边
斜边
sin A=
=
∠A的正弦
∠A的余弦
=
cos A=
∠A的正切
tan A=
=
锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
作业布置
1.如图△ABC中∠C=90°,BC=5, AC=12.
判断:(1)sinA= ( )
(2)tanB= ( )
√
×
A
B
C
2. 如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值( )
A.扩大100倍 B. 缩小100倍
C.不变 D. 不能确定
C
3. 在Rt△ABC中,∠C为Rt∠ .
求证:sin2A+cos2A=1.
证明:∵∠C=Rt∠
∵ AC2+BC2=AB2
∴sinA= ,cosA=
作业布置
4. 如图,在△ABC中,∠ABC=90°,BD⊥AC于D,∠CBD=α,AB=3, BC=4,求sinα,cosα,tanα的值.
作业布置
Thanks!
2
https://www.21cnjy.com/recruitment/home/admin
