平面直角坐标系的应用(3)满分训练 2024-2025学年浙教版八年级数学上册(含答案)
文档属性
| 名称 | 平面直角坐标系的应用(3)满分训练 2024-2025学年浙教版八年级数学上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 291.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 00:00:00 | ||
图片预览


文档简介
平面直角坐标系的应用(3)
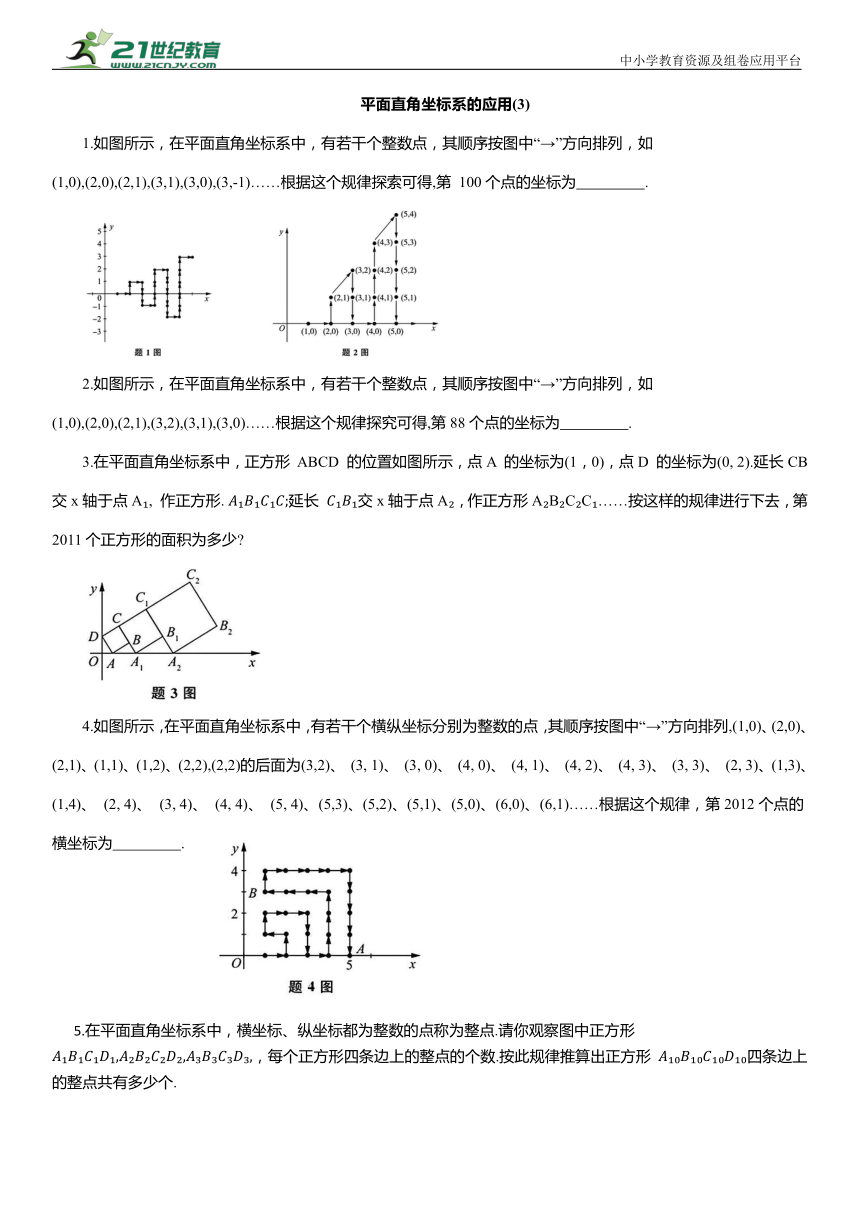
1.如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1)……根据这个规律探索可得,第 100个点的坐标为 .
2.如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)……根据这个规律探究可得,第88个点的坐标为 .
3.在平面直角坐标系中,正方形 ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0, 2).延长CB 交x轴于点A , 作正方形. 延长 交x轴于点A ,作正方形A B C C ……按这样的规律进行下去,第2011个正方形的面积为多少
4.如图所示,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2),(2,2)的后面为(3,2)、 (3, 1)、 (3, 0)、 (4, 0)、 (4, 1)、 (4, 2)、 (4, 3)、 (3, 3)、 (2, 3)、(1,3)、 (1,4)、 (2, 4)、 (3, 4)、 (4, 4)、 (5, 4)、(5,3)、(5,2)、(5,1)、(5,0)、(6,0)、(6,1)……根据这个规律,第2012个点的横坐标为 .
5.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形 ,每个正方形四条边上的整点的个数.按此规律推算出正方形 四条边上的整点共有多少个.
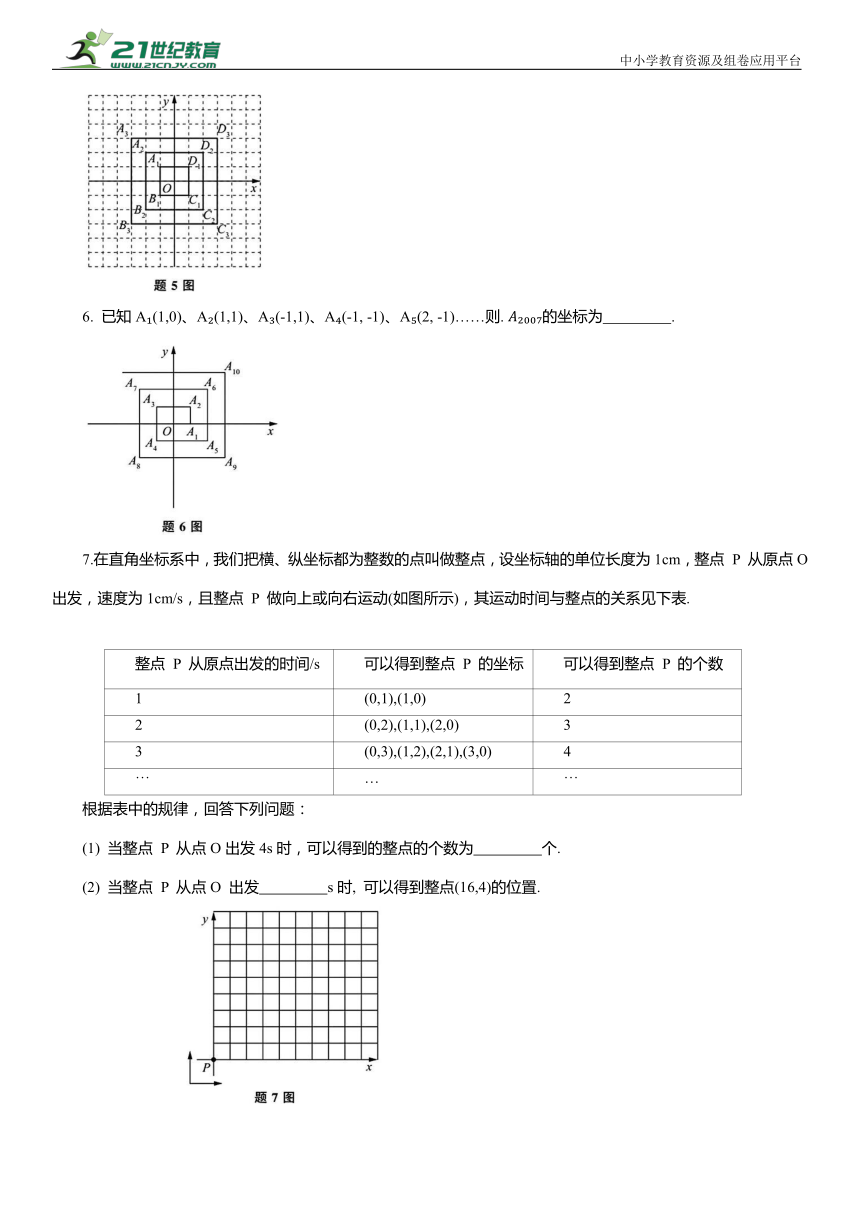
6. 已知A (1,0)、A (1,1)、A (-1,1)、A (-1, -1)、A (2, -1)……则. 的坐标为 .
7.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm,整点 P 从原点O出发,速度为1cm/s,且整点 P 做向上或向右运动(如图所示),其运动时间与整点的关系见下表.
整点 P 从原点出发的时间/s 可以得到整点 P 的坐标 可以得到整点 P 的个数
1 (0,1),(1,0) 2
2 (0,2),(1,1),(2,0) 3
3 (0,3),(1,2),(2,1),(3,0) 4
··· … ···
根据表中的规律,回答下列问题:
(1) 当整点 P 从点O出发4s时,可以得到的整点的个数为 个.
中小学教育资源及组卷应用平台
(2) 当整点 P 从点O 出发 s时, 可以得到整点(16,4)的位置.
8.如图所示,在平面直角坐标系上有个点 P(1,0),点P 第1次向上跳动1个单位至点 P (1,1),紧接着第2次向左跳动2个单位至点 P (-1,1),第3次向上跳动1个单位,第4次向右跳动 3个单位,第5 次又向上跳动1个单位,第6次向左跳动4个单位……依此规律跳动下去,点P 第99次跳动至点 P 的坐标是 ;点 P 第 2009 次 跳 动 至 点 P 的坐标是 .
9.已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度.在平面直角坐标系内,现有一动点 P 第1次从原点O出发按甲方式运动到点P ,第2次从点 P 出发按乙方式运动到点 P ,第3次从点 P 出发再按甲方式运动到点 P ,第4次从点 P 出发再按乙方式运动到点 P ……依此运动规律,则经过第11次运动后,动点 P 所在位置P 的坐标是 .
10.如图所示,一个动点在第一象限内及x轴,y轴上运动,在第1分钟,它从原点运动到(1,0),第2分钟, 从(1,0)运动到(1, 1),然后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,且每分钟运动1个单位长度.当动点所在位置的坐标是(5,5)时,所经过的时间是 分钟,在第1002分钟后,这个动点所在的位置的坐标是
11. 观察下列有规律的点的坐标:
A (1, 1), A (2, - 4), A (3, 4), A (4, - 2), A (5, 7), A (6, - ),A (7,10), A (8, - 1)……
依此规律, A 的坐标为 , A 的坐标为 .
12.设坐标平面内有一个质点从原点出发,沿x 轴跳动,每次向正方向或负方向跳动1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方案共有多少种
答案
1.(14,2).提示:本题的考点在于对平面直角坐标系的熟练运用能力,用“从特殊到一般”的方法入手寻找规律.从图中可以看出,横坐标为1的有一个点,横坐标为2的有2个点,横坐标为3的有3个点……依此类推,横坐标为n的有n个点.题目要求写出第100个点的坐标,我们可以通过加法计算算出第100个点位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式可得到坐标.
2.(13,3).提示:用“从特殊到一般”的方法由图形得出点的个数依次是1、2、3、4、5……且横坐标是偶数时,箭头朝上, 因为1+2+3+4+…+10=55, 所以88-55=33; 因为11+12=23<33, 11+12+13=36>33, 所以88-55-23=10.因此第88个点的横坐标是13,纵坐标是13-10=3, 即第88个点的坐标是(13,3).
提示:本题运用“从特殊到一般”的解题技巧,先根据点A 的坐标为(1,0),点D 的坐标为(0, 2)求出正方形ABCD 的边长为 ,设其面积为 依此类推,接下来的面积依次为S ,S ,S ……第2011个正方形的面积为 S ,又因为三角形相似,所以 由此得 所以
4.45.提示:当n为一个奇数平方时,设 则第n个点坐标为(m,0),第(n-1)个为(m,1),第(n-2)个为(m, 2)……到第(n-m)个前都符合该规律, ,所以第 2012 个点的坐标为(45,13).同理, 当n 为一个偶数平方时,设 则第n个点坐标为(1, m-1), 第(n+1)个为(1, m),第n+2个为(2,m)……找到如点 A 或点B 这样的关键点的坐标,问题就容易解决了.观察图形可知,本题也运用“从特殊到一般”的解题技巧,到每一横坐标相同的点结束,点的总个数等于最后点的横坐标的平方,并且横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当横坐标是偶数时,以横坐标为1,纵坐标为横坐标减1的点结束,根据此规律解答即可.如:横坐标为1的点结束,共有1个,横坐标为2的点结束,共有2个,横坐标为3的点结束,共有9个,横坐标为4的点结束,共有16个,……横坐标为n的点结束,共有n 个,第2025个点是(45,0),第2012个点是(45,13), 所以,第2012个点的横坐标为45.
5.80.提示:根据题意,根据“从特殊到一般”找规律,可知,A B C D 四条边上的整点共有8个,即4+4×1=8,A B C D 四条边上的整点共有16个, 即4+4×3=16,正方形A B C D 四条边上的整点的个数有4+4×5=24……依此类推,正方形A B C D 四条边上的整点的个数有4+4×19=80.
6.(-502,502).提示: 根据题意, 得第一象限里的点分别是A , A ,A ……第二象限里的点分别是A ,A ,A ……第三象限里的点分别是A ,A ,A ……第四象限里的点分别是A ,A , A ……由此可见,点A 是在第二象限内,而第二象限内点的横坐标是负数,纵坐标是正数,且绝对值相等,并且由观察、推理、归纳得到A (-1,1),A (-2,2),A (-3,3)……因为2007=4×501……3,所以点A 的坐标应该是(-502, 502).
7.5,20.提示:(1)根据表格中的规律可知,当点 P 从点O出发4s时,可得到整点 P 的坐标为(0,4),(1,3),(2,2),(3,1),(4,0),共5个.(2)从表格规律知当整点 P 从原点O出发的时间为 ns时,可得整点 P 的坐标为(x,y),则x+y=n,因为16+4=20,所以当整点 P 从点O出发20s时,可到达整点(16,4)的位置.
8.(-25,49),(-502,1005).提示:设点 Pm的横坐标的绝对值是n, 则在 y轴右侧的点的下标分别是4n-1和4n-3,在y轴左侧的点的下标是4n-2和4n-1;判断 P 的坐标,就是看99=4n-1,99=4n-3,99=4n-2和99=4n-1这四个式子中哪一个有正整数解,从而判断出点的横坐标.由以上分析可得,点 P 第99次跳动至点 P 的坐标是(-25,49);点 P 第 2009次跳动至点 P 的坐标是(-502,1005).
9.(-3,-4).提示:先根据 P 点运动的规律求出经过第11次运动后分别向甲、向乙运动的次数,再分别求出其横纵坐标即可.由题意,动点 P 经过第11次运动,那么向甲运动了6次,向乙运动了5次,横坐标即为2×6-3×5=-3,纵坐标为1×6-2×5=-4, 即P 的坐标是(-3,-4).
10.30,(21,31).提示:从题目可以得出规律,动点运动的速度是每分钟运动1个单位长度,(0,0)→(1,0)→(1,1)→(0,1)用的时间分别是1分钟,2分钟,3分钟,到(0,2)用4分钟,到(2,2)用6分钟,到(2,0)用8分钟,到(3,0)用9分钟,到(3,3)用12分钟,到(0,4)用16分钟……依此类推,到(5,5)用30分钟.由上面的结论,我们可以得到在第一象限角平分线上的点从(1,1)用2分钟到(2,2)用6分钟,到(3,3)用12分钟,则由(n,n)到(n+1,n+1)时间增加2n+2分钟.故当动点所在位置的坐标是(5,5)时,所经过的时间是30分钟,在第1002分钟后,这个动点所在的位置的坐标是(21,31).
11.(11, 16), 提示:观察各点的坐标可以得到以下规律,点的横坐标的值等于对应的点下标的数值.当下标是奇数时,纵坐标是正数,后一偶数项的纵坐标依次比前一偶数项的纵坐标多3,故A 的坐标为(11,16);当下标是偶数时,纵坐标是负数,后一偶数项的纵坐标依次为前一偶数项的纵坐标的 故A 的坐标为
12.5种.提示:
①可先向负方向跳动一次再连续向正方向跳动4次;
②向正方向跳动1次,再向负方向跳动1次,再向正方向跳动3次;
③向正方向跳动2次后,再向负方向跳动1次,再向正方向跳动2;
④向正方向跳动3次后,再向负方向跳动1次,再向正方向跳动1次;
⑤向正方向跳动4次后,再向负方向跳动1次.
1.如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0),(3,-1)……根据这个规律探索可得,第 100个点的坐标为 .
2.如图所示,在平面直角坐标系中,有若干个整数点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(3,2),(3,1),(3,0)……根据这个规律探究可得,第88个点的坐标为 .
3.在平面直角坐标系中,正方形 ABCD 的位置如图所示,点A 的坐标为(1,0),点D 的坐标为(0, 2).延长CB 交x轴于点A , 作正方形. 延长 交x轴于点A ,作正方形A B C C ……按这样的规律进行下去,第2011个正方形的面积为多少
4.如图所示,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,(1,0)、(2,0)、(2,1)、(1,1)、(1,2)、(2,2),(2,2)的后面为(3,2)、 (3, 1)、 (3, 0)、 (4, 0)、 (4, 1)、 (4, 2)、 (4, 3)、 (3, 3)、 (2, 3)、(1,3)、 (1,4)、 (2, 4)、 (3, 4)、 (4, 4)、 (5, 4)、(5,3)、(5,2)、(5,1)、(5,0)、(6,0)、(6,1)……根据这个规律,第2012个点的横坐标为 .
5.在平面直角坐标系中,横坐标、纵坐标都为整数的点称为整点.请你观察图中正方形 ,每个正方形四条边上的整点的个数.按此规律推算出正方形 四条边上的整点共有多少个.
6. 已知A (1,0)、A (1,1)、A (-1,1)、A (-1, -1)、A (2, -1)……则. 的坐标为 .
7.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点,设坐标轴的单位长度为1cm,整点 P 从原点O出发,速度为1cm/s,且整点 P 做向上或向右运动(如图所示),其运动时间与整点的关系见下表.
整点 P 从原点出发的时间/s 可以得到整点 P 的坐标 可以得到整点 P 的个数
1 (0,1),(1,0) 2
2 (0,2),(1,1),(2,0) 3
3 (0,3),(1,2),(2,1),(3,0) 4
··· … ···
根据表中的规律,回答下列问题:
(1) 当整点 P 从点O出发4s时,可以得到的整点的个数为 个.
中小学教育资源及组卷应用平台
(2) 当整点 P 从点O 出发 s时, 可以得到整点(16,4)的位置.
8.如图所示,在平面直角坐标系上有个点 P(1,0),点P 第1次向上跳动1个单位至点 P (1,1),紧接着第2次向左跳动2个单位至点 P (-1,1),第3次向上跳动1个单位,第4次向右跳动 3个单位,第5 次又向上跳动1个单位,第6次向左跳动4个单位……依此规律跳动下去,点P 第99次跳动至点 P 的坐标是 ;点 P 第 2009 次 跳 动 至 点 P 的坐标是 .
9.已知甲运动方式为:先竖直向上运动1个单位长度后,再水平向右运动2个单位长度;乙运动方式为:先竖直向下运动2个单位长度后,再水平向左运动3个单位长度.在平面直角坐标系内,现有一动点 P 第1次从原点O出发按甲方式运动到点P ,第2次从点 P 出发按乙方式运动到点 P ,第3次从点 P 出发再按甲方式运动到点 P ,第4次从点 P 出发再按乙方式运动到点 P ……依此运动规律,则经过第11次运动后,动点 P 所在位置P 的坐标是 .
10.如图所示,一个动点在第一象限内及x轴,y轴上运动,在第1分钟,它从原点运动到(1,0),第2分钟, 从(1,0)运动到(1, 1),然后它接着按图中箭头所示在与x轴,y轴平行的方向来回运动,且每分钟运动1个单位长度.当动点所在位置的坐标是(5,5)时,所经过的时间是 分钟,在第1002分钟后,这个动点所在的位置的坐标是
11. 观察下列有规律的点的坐标:
A (1, 1), A (2, - 4), A (3, 4), A (4, - 2), A (5, 7), A (6, - ),A (7,10), A (8, - 1)……
依此规律, A 的坐标为 , A 的坐标为 .
12.设坐标平面内有一个质点从原点出发,沿x 轴跳动,每次向正方向或负方向跳动1个单位,经过5次跳动质点落在点(3,0)(允许重复过此点)处,则质点不同的运动方案共有多少种
答案
1.(14,2).提示:本题的考点在于对平面直角坐标系的熟练运用能力,用“从特殊到一般”的方法入手寻找规律.从图中可以看出,横坐标为1的有一个点,横坐标为2的有2个点,横坐标为3的有3个点……依此类推,横坐标为n的有n个点.题目要求写出第100个点的坐标,我们可以通过加法计算算出第100个点位于第几列第几行,然后对应得出坐标规律,将行列数代入规律式可得到坐标.
2.(13,3).提示:用“从特殊到一般”的方法由图形得出点的个数依次是1、2、3、4、5……且横坐标是偶数时,箭头朝上, 因为1+2+3+4+…+10=55, 所以88-55=33; 因为11+12=23<33, 11+12+13=36>33, 所以88-55-23=10.因此第88个点的横坐标是13,纵坐标是13-10=3, 即第88个点的坐标是(13,3).
提示:本题运用“从特殊到一般”的解题技巧,先根据点A 的坐标为(1,0),点D 的坐标为(0, 2)求出正方形ABCD 的边长为 ,设其面积为 依此类推,接下来的面积依次为S ,S ,S ……第2011个正方形的面积为 S ,又因为三角形相似,所以 由此得 所以
4.45.提示:当n为一个奇数平方时,设 则第n个点坐标为(m,0),第(n-1)个为(m,1),第(n-2)个为(m, 2)……到第(n-m)个前都符合该规律, ,所以第 2012 个点的坐标为(45,13).同理, 当n 为一个偶数平方时,设 则第n个点坐标为(1, m-1), 第(n+1)个为(1, m),第n+2个为(2,m)……找到如点 A 或点B 这样的关键点的坐标,问题就容易解决了.观察图形可知,本题也运用“从特殊到一般”的解题技巧,到每一横坐标相同的点结束,点的总个数等于最后点的横坐标的平方,并且横坐标是奇数时最后以横坐标为该数,纵坐标为0结束,当横坐标是偶数时,以横坐标为1,纵坐标为横坐标减1的点结束,根据此规律解答即可.如:横坐标为1的点结束,共有1个,横坐标为2的点结束,共有2个,横坐标为3的点结束,共有9个,横坐标为4的点结束,共有16个,……横坐标为n的点结束,共有n 个,第2025个点是(45,0),第2012个点是(45,13), 所以,第2012个点的横坐标为45.
5.80.提示:根据题意,根据“从特殊到一般”找规律,可知,A B C D 四条边上的整点共有8个,即4+4×1=8,A B C D 四条边上的整点共有16个, 即4+4×3=16,正方形A B C D 四条边上的整点的个数有4+4×5=24……依此类推,正方形A B C D 四条边上的整点的个数有4+4×19=80.
6.(-502,502).提示: 根据题意, 得第一象限里的点分别是A , A ,A ……第二象限里的点分别是A ,A ,A ……第三象限里的点分别是A ,A ,A ……第四象限里的点分别是A ,A , A ……由此可见,点A 是在第二象限内,而第二象限内点的横坐标是负数,纵坐标是正数,且绝对值相等,并且由观察、推理、归纳得到A (-1,1),A (-2,2),A (-3,3)……因为2007=4×501……3,所以点A 的坐标应该是(-502, 502).
7.5,20.提示:(1)根据表格中的规律可知,当点 P 从点O出发4s时,可得到整点 P 的坐标为(0,4),(1,3),(2,2),(3,1),(4,0),共5个.(2)从表格规律知当整点 P 从原点O出发的时间为 ns时,可得整点 P 的坐标为(x,y),则x+y=n,因为16+4=20,所以当整点 P 从点O出发20s时,可到达整点(16,4)的位置.
8.(-25,49),(-502,1005).提示:设点 Pm的横坐标的绝对值是n, 则在 y轴右侧的点的下标分别是4n-1和4n-3,在y轴左侧的点的下标是4n-2和4n-1;判断 P 的坐标,就是看99=4n-1,99=4n-3,99=4n-2和99=4n-1这四个式子中哪一个有正整数解,从而判断出点的横坐标.由以上分析可得,点 P 第99次跳动至点 P 的坐标是(-25,49);点 P 第 2009次跳动至点 P 的坐标是(-502,1005).
9.(-3,-4).提示:先根据 P 点运动的规律求出经过第11次运动后分别向甲、向乙运动的次数,再分别求出其横纵坐标即可.由题意,动点 P 经过第11次运动,那么向甲运动了6次,向乙运动了5次,横坐标即为2×6-3×5=-3,纵坐标为1×6-2×5=-4, 即P 的坐标是(-3,-4).
10.30,(21,31).提示:从题目可以得出规律,动点运动的速度是每分钟运动1个单位长度,(0,0)→(1,0)→(1,1)→(0,1)用的时间分别是1分钟,2分钟,3分钟,到(0,2)用4分钟,到(2,2)用6分钟,到(2,0)用8分钟,到(3,0)用9分钟,到(3,3)用12分钟,到(0,4)用16分钟……依此类推,到(5,5)用30分钟.由上面的结论,我们可以得到在第一象限角平分线上的点从(1,1)用2分钟到(2,2)用6分钟,到(3,3)用12分钟,则由(n,n)到(n+1,n+1)时间增加2n+2分钟.故当动点所在位置的坐标是(5,5)时,所经过的时间是30分钟,在第1002分钟后,这个动点所在的位置的坐标是(21,31).
11.(11, 16), 提示:观察各点的坐标可以得到以下规律,点的横坐标的值等于对应的点下标的数值.当下标是奇数时,纵坐标是正数,后一偶数项的纵坐标依次比前一偶数项的纵坐标多3,故A 的坐标为(11,16);当下标是偶数时,纵坐标是负数,后一偶数项的纵坐标依次为前一偶数项的纵坐标的 故A 的坐标为
12.5种.提示:
①可先向负方向跳动一次再连续向正方向跳动4次;
②向正方向跳动1次,再向负方向跳动1次,再向正方向跳动3次;
③向正方向跳动2次后,再向负方向跳动1次,再向正方向跳动2;
④向正方向跳动3次后,再向负方向跳动1次,再向正方向跳动1次;
⑤向正方向跳动4次后,再向负方向跳动1次.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
