三角形辅助线添加综合满分训练 2024-2025学年浙教版八年级数学上册(含答案)
文档属性
| 名称 | 三角形辅助线添加综合满分训练 2024-2025学年浙教版八年级数学上册(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 432.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-16 07:17:24 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
三角形辅助线添加综合
1.(1)求证:等边三角形内的任意一点到两腰的距离之和等于定长.(提示:添加辅助线证明)
(2)如图所示, 在三角形ABC中,点 D 是三角形内一点,连接DA、DB、DC,若AB=AC,∠ADB=∠ADC,求证:AD平分.
2.如图所示, 分别是以AB、AC 为边的等边三角形,连接CD、BE,它们相交于点 O,再连接OA.求证:OA 是 的角平分线.
3. 已知 ,BF、CE 交于点M, 连接AM.
(1)求证:
(2) 求∠AMC 的度数.
4.在直角三角形 ABC 中, 分别以 AB、AC 为边在 外侧作等边 和等边 DE 交AB 于点F,求证:
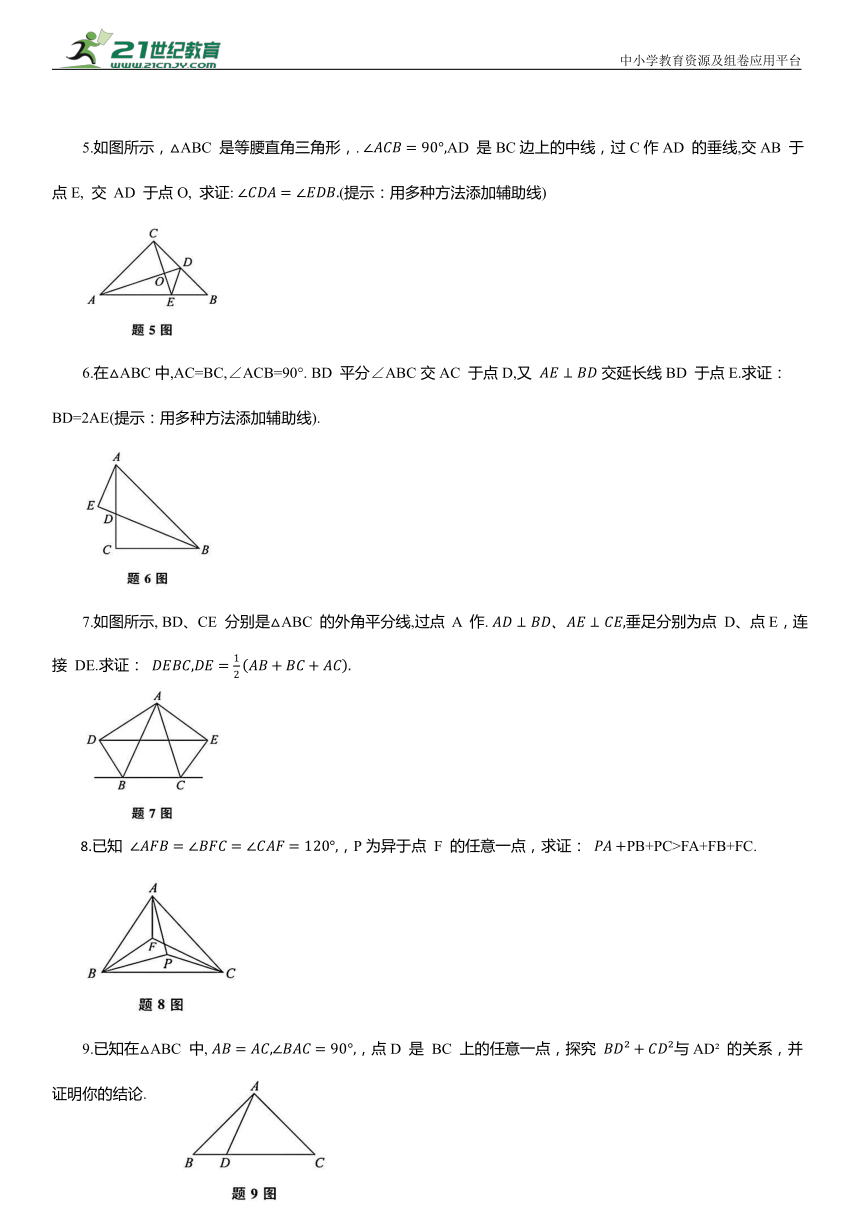
5.如图所示,△ABC 是等腰直角三角形,. AD 是BC边上的中线,过C作AD 的垂线,交AB 于点E, 交 AD 于点O, 求证: (提示:用多种方法添加辅助线)
6.在△ABC中,AC=BC,∠ACB=90°. BD 平分∠ABC交AC 于点D,又 交延长线BD 于点E.求证:BD=2AE(提示:用多种方法添加辅助线).
7.如图所示, BD、CE 分别是△ABC 的外角平分线,过点 A 作. 垂足分别为点 D、点E,连接 DE.求证:
8.已知 ,P为异于点 F 的任意一点,求证: PB+PC>FA+FB+FC.
9.已知在△ABC 中, ,点D 是 BC 上的任意一点,探究 与AD 的关系,并证明你的结论.
10.点 P 为△ABC 内一点, 若AP⊥BC, 证明: .(补充: 使用勾股定理, 即在 Rt△ABC 中, 则
答案
1.提示:(1)(面积法)本题先根据已知条件画图,已知点 P 是等边三角形ABC内的任意一点,过点 P分别作三边的垂线,分别交三边于点 D、点E、点F.求证 PD+PE+PF 为定长.
证明:过点A 作AG⊥BC,垂足为点G,分别连接AP、BP、CP.因为 易得PD+PE+PF=AG 为定长.因此,等边三角形内的任意一点到两腰的距离之和等于定长.
(2)(面积法)过点 A 作AE⊥BD 交BD 延长线于点E, 再过点A 作AF⊥CD 交CD 延长线于点F.因为∠ADB=∠ADC,所以∠ADE=∠ADF,因此△ADF≌△ADE(AAS),得到AF=AE.进而△AFC≌△AEB,得到∠ABD=∠ACD,因此∠BAD=∠CAD, 即AD平分∠BAC.
2.提示:(面积法)由已知条件易得△BAE≌△DAC(SAS),所以CD=BE.过点 A 作AM⊥DC 于点 M, 作 AN⊥BE 于点N, 所以AM=AN.又由AM⊥DC于点M,AN⊥BE 于点N,所以点A在∠DOE 的角平分线上(角平分线定理),即 OA 是∠DOE 的角平分线.
3.提示:(1)由条件易得∠CAE=∠BAF,从而得到△ABF≌△ACE(SAS).因此BF=CE,∠ACE=∠ABF,所以∠ACE+∠ACB+∠CBF=∠ABF+∠ACB+∠CBF=90°,所以∠CMB=90°, 即BF⊥CE.
(2)作AH⊥CE 于点H,AG⊥BF 于点G.由(1)所得结论得到△ABG≌△ACH(ASA),所以AG=AH, ∠AMG=45°, 因此∠AMC=135°.
4.提示:(垂直法)过点 E 作EG⊥AB 于点G.因为△ABE 是等边三角形, 又因为 Rt△ABC 中 (直角三角形 30°的角所对的边等于斜边的一半),所以△ACB≌△EGA(SAS),得到EG=AC.从而得到∠DAF=∠DAC+∠CAB=90°, 所以△ADF≌△GEF(AAS),因此EF=FD.
5.提示:(解法一 垂直法)如图(1)所示,过点 B 作BF⊥CB,交CE 的延长线于点F,连接DE.由条件易得△ACD≌△CBF(ASA),从而得到∠ADC=∠CFB,BD=BF=CD,得△DBE≌△FBE(SAS),因此∠CDA=∠EDB.
(解法二 角平分线法)如图(2)所示, 作∠ACB的平分线CG交AD 于点G.由条件AC=BC,∠ACG=∠BCG=45°,∠CAD=∠BCE,可证得△AGC≌△CEB(AAS), 从而得到CG=BE.由条件CG=BE,CD=BD,∠DCG=∠BDE=45°,证得△DCG≌△EBD,因此∠CDA=∠EDB.
6.提示:(解法一 补形法)如图(1)所示, 延长AE、BC 交于点F.由条件易得△AEB≌△FEB(ASA),所以AF=2AE.因为BE⊥AE,∠BDC=∠ADE,所以∠CAF=∠CBD(同角的余角相等),得到△CAF≌△CBD(ASA),所以BD=AF,因此BD=2AE.
(解法二)如图(2)所示, 过点 D作DF∥AB,交BC于点F,过点 F作FH⊥BD,垂足为点 H.由条件易得∠CFD=∠CBA=45°,∠FDB=∠CBD=∠ABD,所以FB=FD,从而得到 FH 是BD 的中垂线,
又CD=FC,AC=BC,所以BF=AD,得△BFH≌△ADE,得到BH=AE,因此BD=2AE.
7.提示:(补形法)如图所示, 延长AD、AE 交直线BC 于点F、点G.由条件易得∠ADB=∠FDB=90°,得到△ABD≌△FBD, 从而得到 AB=FB, AD =FD. 同理, AC=CG, AE =EG, 所以DE∥BC.因此 所以
三角形辅助线添加综合
1.(1)求证:等边三角形内的任意一点到两腰的距离之和等于定长.(提示:添加辅助线证明)
(2)如图所示, 在三角形ABC中,点 D 是三角形内一点,连接DA、DB、DC,若AB=AC,∠ADB=∠ADC,求证:AD平分.
2.如图所示, 分别是以AB、AC 为边的等边三角形,连接CD、BE,它们相交于点 O,再连接OA.求证:OA 是 的角平分线.
3. 已知 ,BF、CE 交于点M, 连接AM.
(1)求证:
(2) 求∠AMC 的度数.
4.在直角三角形 ABC 中, 分别以 AB、AC 为边在 外侧作等边 和等边 DE 交AB 于点F,求证:
5.如图所示,△ABC 是等腰直角三角形,. AD 是BC边上的中线,过C作AD 的垂线,交AB 于点E, 交 AD 于点O, 求证: (提示:用多种方法添加辅助线)
6.在△ABC中,AC=BC,∠ACB=90°. BD 平分∠ABC交AC 于点D,又 交延长线BD 于点E.求证:BD=2AE(提示:用多种方法添加辅助线).
7.如图所示, BD、CE 分别是△ABC 的外角平分线,过点 A 作. 垂足分别为点 D、点E,连接 DE.求证:
8.已知 ,P为异于点 F 的任意一点,求证: PB+PC>FA+FB+FC.
9.已知在△ABC 中, ,点D 是 BC 上的任意一点,探究 与AD 的关系,并证明你的结论.
10.点 P 为△ABC 内一点, 若AP⊥BC, 证明: .(补充: 使用勾股定理, 即在 Rt△ABC 中, 则
答案
1.提示:(1)(面积法)本题先根据已知条件画图,已知点 P 是等边三角形ABC内的任意一点,过点 P分别作三边的垂线,分别交三边于点 D、点E、点F.求证 PD+PE+PF 为定长.
证明:过点A 作AG⊥BC,垂足为点G,分别连接AP、BP、CP.因为 易得PD+PE+PF=AG 为定长.因此,等边三角形内的任意一点到两腰的距离之和等于定长.
(2)(面积法)过点 A 作AE⊥BD 交BD 延长线于点E, 再过点A 作AF⊥CD 交CD 延长线于点F.因为∠ADB=∠ADC,所以∠ADE=∠ADF,因此△ADF≌△ADE(AAS),得到AF=AE.进而△AFC≌△AEB,得到∠ABD=∠ACD,因此∠BAD=∠CAD, 即AD平分∠BAC.
2.提示:(面积法)由已知条件易得△BAE≌△DAC(SAS),所以CD=BE.过点 A 作AM⊥DC 于点 M, 作 AN⊥BE 于点N, 所以AM=AN.又由AM⊥DC于点M,AN⊥BE 于点N,所以点A在∠DOE 的角平分线上(角平分线定理),即 OA 是∠DOE 的角平分线.
3.提示:(1)由条件易得∠CAE=∠BAF,从而得到△ABF≌△ACE(SAS).因此BF=CE,∠ACE=∠ABF,所以∠ACE+∠ACB+∠CBF=∠ABF+∠ACB+∠CBF=90°,所以∠CMB=90°, 即BF⊥CE.
(2)作AH⊥CE 于点H,AG⊥BF 于点G.由(1)所得结论得到△ABG≌△ACH(ASA),所以AG=AH, ∠AMG=45°, 因此∠AMC=135°.
4.提示:(垂直法)过点 E 作EG⊥AB 于点G.因为△ABE 是等边三角形, 又因为 Rt△ABC 中 (直角三角形 30°的角所对的边等于斜边的一半),所以△ACB≌△EGA(SAS),得到EG=AC.从而得到∠DAF=∠DAC+∠CAB=90°, 所以△ADF≌△GEF(AAS),因此EF=FD.
5.提示:(解法一 垂直法)如图(1)所示,过点 B 作BF⊥CB,交CE 的延长线于点F,连接DE.由条件易得△ACD≌△CBF(ASA),从而得到∠ADC=∠CFB,BD=BF=CD,得△DBE≌△FBE(SAS),因此∠CDA=∠EDB.
(解法二 角平分线法)如图(2)所示, 作∠ACB的平分线CG交AD 于点G.由条件AC=BC,∠ACG=∠BCG=45°,∠CAD=∠BCE,可证得△AGC≌△CEB(AAS), 从而得到CG=BE.由条件CG=BE,CD=BD,∠DCG=∠BDE=45°,证得△DCG≌△EBD,因此∠CDA=∠EDB.
6.提示:(解法一 补形法)如图(1)所示, 延长AE、BC 交于点F.由条件易得△AEB≌△FEB(ASA),所以AF=2AE.因为BE⊥AE,∠BDC=∠ADE,所以∠CAF=∠CBD(同角的余角相等),得到△CAF≌△CBD(ASA),所以BD=AF,因此BD=2AE.
(解法二)如图(2)所示, 过点 D作DF∥AB,交BC于点F,过点 F作FH⊥BD,垂足为点 H.由条件易得∠CFD=∠CBA=45°,∠FDB=∠CBD=∠ABD,所以FB=FD,从而得到 FH 是BD 的中垂线,
又CD=FC,AC=BC,所以BF=AD,得△BFH≌△ADE,得到BH=AE,因此BD=2AE.
7.提示:(补形法)如图所示, 延长AD、AE 交直线BC 于点F、点G.由条件易得∠ADB=∠FDB=90°,得到△ABD≌△FBD, 从而得到 AB=FB, AD =FD. 同理, AC=CG, AE =EG, 所以DE∥BC.因此 所以
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
