第三章 数据分析初步（含答案）

中小学教育资源及组卷应用平台
第三章 数据分析初步
一、单选题
1．如图是甲、乙两位同学在参加体育中考前的5次体能测试成绩折线统计图，下列说法正确的是（　　）
A．甲的平均成绩较低且稳定 B．乙的平均成绩较低且稳定
C．甲的平均成绩较高且稳定 D．乙的平均成绩较高且稳定
2．某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：
尺码 39 40 41 42 43
平均每天销售数量/件 10 12 20 12 12
该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（　　）
A．平均数 B．方差 C．众数 D．中位数
3．在共有人参加的“我爱祖国”演讲比赛中，参赛选手要想知道自己是否能进入前8名．只需要了解自己的成绩以及全部成绩的（　　）
A．平均数 B．众数
C．中位数 D．最高分与最低分的差
4．甲，乙，丙，丁四个小组的同学分别参加了班级组织的中华古诗词知识竞赛，四个小组的平均分相同，其方差如下表．若要从中选出一个成绩更稳定的小组参加年级的比赛，那么应选（　　）
组名 甲 乙 丙 丁
方差 4.3 3.2 4 3.6
A．甲 B．乙 C．丙 D．丁
5．数据：2，3，5，7，8，8的中位数是（　　）
A．5 B．6 C．7 D．8
6．下列说法中，正确的是（）
A．一组数据的众数一定只有一个．
B．一组数据的众数是6，则这组数据中出现次数最多的数据是6．
C．一组数据的中位数一定是这组数据中的某一个数据．
D．一组数据中的最大的数据增大时，这组数据的中位数也随之增大．
7．某同学对一组数据23，31，32，43，32，5◆，52进行统计分析时，发现其中一个两位数的个位数字被污染看不到了，则下列计算结果一定与被污数字无关的是（　　）
A．平均数 B．中位数 C．方差 D．众数
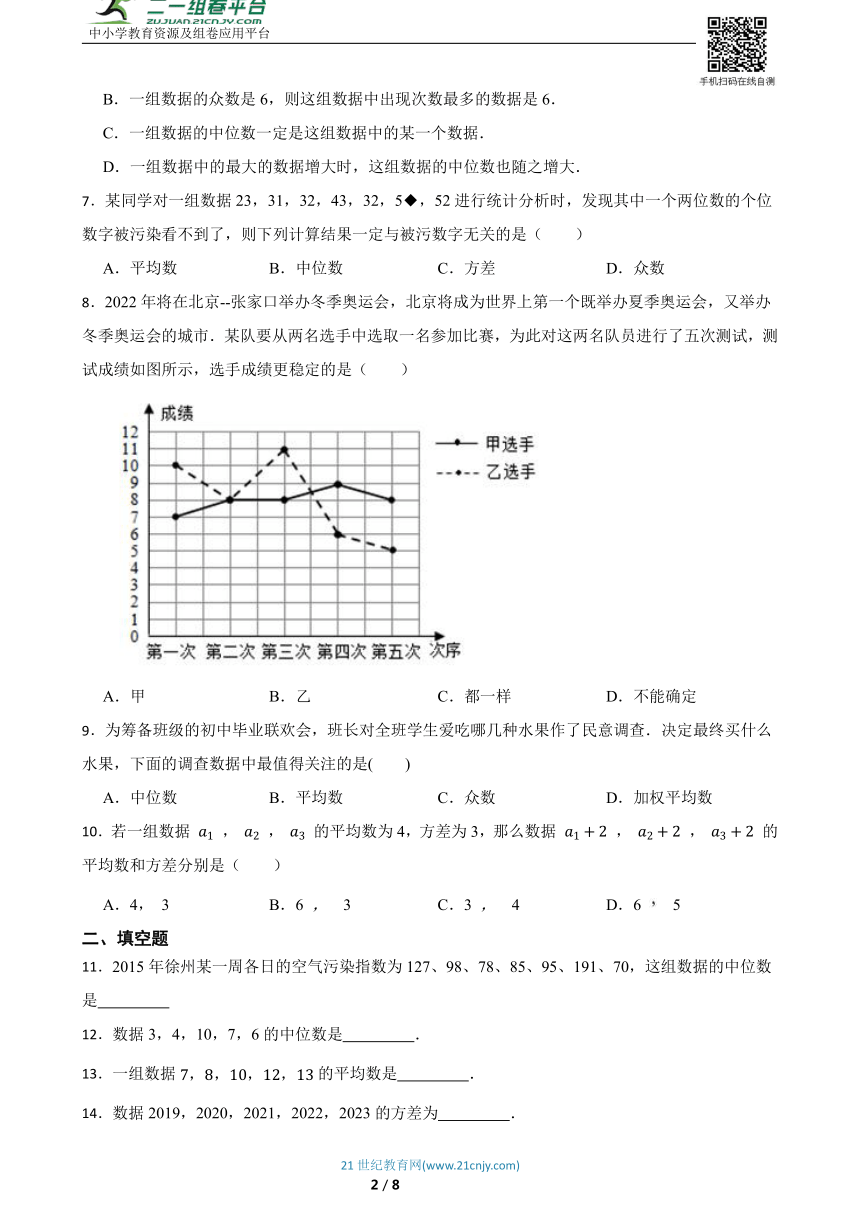
8．2022年将在北京--张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市．某队要从两名选手中选取一名参加比赛，为此对这两名队员进行了五次测试，测试成绩如图所示，选手成绩更稳定的是（　　）
A．甲 B．乙 C．都一样 D．不能确定
9．为筹备班级的初中毕业联欢会，班长对全班学生爱吃哪几种水果作了民意调查．决定最终买什么水果，下面的调查数据中最值得关注的是(　　)
A．中位数 B．平均数 C．众数 D．加权平均数
10．若一组数据 ， ， 的平均数为4，方差为3，那么数据 ， ， 的平均数和方差分别是（　　）
A．4， 3 B．6 3 C．3 4 D．6 5
二、填空题
11．2015年徐州某一周各日的空气污染指数为127、98、78、85、95、191、70，这组数据的中位数是　 　
12．数据3，4，10，7，6的中位数是　 　．
13．一组数据的平均数是　 　．
14．数据2019，2020，2021，2022，2023的方差为　 　．
15．甲、乙两台机器分别罐装每瓶标准质量为500克的矿泉水，从甲、乙两台机器罐装的矿泉水中分别随机抽取了30瓶，测算得它们实际质量的方差是 =4.8， =3.6，则　 　(填“甲”或“乙”)机器罐装的矿泉水质量比较稳定.
16．定义新运算：[a，b，c]＝a（c＜a＜b），即[a，b，c]的取值为a，b，c的中位数，例如，[1，2，3]＝2，[3，4，8]＝4，已知函数y＝[x+2，x2+1，﹣x+2]与直线y＝x+b有3个交点时，则b的值为　 　．
三、计算题
17．浙江某大学部分专业采用“三位一体”的形式进行招生，现有甲、乙两名学生，他们各自的三类成绩如表所示：
学生 学业水平测试 综合测试成绩 高考成绩
甲 85 89 81
乙 88 81 83
（1）计算两人的平均成绩，这两人的平均分谁高？
（2）“三位一体”根据入围考生志愿，对学生学业水平测试、综合测试成绩、高考成绩分别赋予权重1∶1∶3，那么这两人的平均分谁高？
18．为了提高体育中考成绩，体育老师组织同学们进行了跳绳项目的训练．小明和小聪最近8次一分钟跳绳的成绩如下：
　 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次
小明 200 180 195 196 182 174 190 195
小聪 190 189 190 192 192 187 192 180
（1）分别求出小明、小聪跳绳的中位数、众数．
（2）通过计算说明，哪位同学的跳绳成绩比较稳定？
四、解答题
19．4月23日是世界读书日，某校为了解同学们的课外阅读情况，随机抽取20名同学，对每人每周用于课外阅读的平均时间（单位：）进行调查，过程如下：
收集数据：
30 60 81 50 40 110 130 146 90 100
60 81 120 140 70 81 10 20 100 81
整理数据：
时间x（）
人数 3 a 8 b
分析数据：
平均数 中位数 众数
80 m 81
请根据以上提供的信息，解答下列问题：
（1）填空：______，______；______；
（2）已知该校学生500人，若每人每周用于课外阅读的平均时间不少于为达标，请估计达标的学生数；
（3）设阅读一本课外书的平均时间为，请选择适当的统计量，估计该校学生每人一年（按52周计）平均阅读多少本课外书？
20．完成下列各题：
（1）一项工程，甲单独做完成，乙单独做完成，甲、乙两人一起完成这项工程需要多长时间？
（2）八年级一班在一次测试中，某题（满分为5分）的得分情况如图所示，计算这题得分的众数、中位数和平均数．
21．随着人们环保意识的增强，电动汽车作为一种绿色交通工具越来越受到消费者的青睐．小明打算从某汽车租赁公司租一辆纯电动汽车使用一天，预计总行程约为420km.该汽车租赁公司有A，B、C三种型号纯电动汽车，每天的租金分别为300元/辆，380元/辆，500元/辆．为了选择合适的型号，小明对三种型号的汽车满电续航里程进行了调查分析，过程如下：
【整理数据】
（1）小明共调查了 辆A 型纯电动汽车，并补全上述的条形统计图；
（2）在A 型纯电动汽车满电续航里程的扇形统计图中， “390km”对应的圆心角度数为　 　
（3）【分析数据】
型号 平均里程（km） 中位数（km） 众数（km）
A 400 400 410
B 432 m 440
C 453 450 n
由上表填空：m=　 　， n=　 　
（4）【判断决策】
结合上述分析，你认为小明选择哪个型号的纯电动汽车较为合适，并说明理由.
22．已知一组数据：x，10，12，6的中位数与平均数相等，求x的值。
答案解析部分
1．【答案】A
【知识点】折线统计图；方差
2．【答案】C
【知识点】统计表；常用统计量的选择
3．【答案】C
【知识点】中位数
4．【答案】B
【知识点】方差
5．【答案】B
【知识点】中位数
6．【答案】B
【知识点】分析数据的集中趋势（平均数、中位数、众数）；真命题与假命题
7．【答案】B
【知识点】分析数据的集中趋势（平均数、中位数、众数）
8．【答案】A
【知识点】折线统计图；方差
9．【答案】C
【知识点】常用统计量的选择
10．【答案】B
【知识点】平均数及其计算；方差
11．【答案】95
【知识点】中位数
12．【答案】6
【知识点】中位数
13．【答案】10
【知识点】平均数及其计算
14．【答案】2
【知识点】方差
15．【答案】乙
【知识点】分析数据的波动程度
16．【答案】或b＝2
【知识点】中位数
17．【答案】（1）甲同学平均分更高；
（2）乙同学的平均分更高．
【知识点】平均数及其计算；加权平均数及其计算
18．【答案】（1）小明的中位数是192.5，众数是195；小聪的中位数是190，众数是192
（2）小聪同学的跳绳成绩比较稳定
【知识点】中位数；方差；众数
19．【答案】（1），，
（2）300人
（3）16本
【知识点】频数（率）分布表；中位数；众数
20．【答案】（1）
（2）众数为3分，中位数为3分，平均数为分
【知识点】加权平均数及其计算；中位数；众数
21．【答案】（1）解：20；
故续航里程400km的车辆数为20-3-4-6-2=5辆，
补全条件统计图如下所示：
（2）72°
（3）430；450
（4）解： 小明打算从某汽车租赁公司租一辆纯电动汽车使用一天，预计总行程约为420km，故A型号的平均数、中位数和众数均低于420，不符合要求；B、C型号符合要求，但B型号的租金比C型号的租金优惠，所以选择B型号的纯电动汽车较为合适．
【知识点】扇形统计图；条形统计图；折线统计图；分析数据的集中趋势（平均数、中位数、众数）
22．【答案】解：当时，这组数据按从小到大顺序排列为x，6，10，12
由题意得
则
当时，这组数据按从小到大顺序排列为6，x，10，12
由题意得
则
当时，这组数据按从小到大顺序排列为6，10，x，12
由题意得
则(舍)
当时，这组数据按从小到大顺序排列为6，10，12，x
由题意得
则
综上所述：x=4或8或16.
【知识点】平均数及其计算；中位数
21世纪教育网(www.21cnjy.com)
1 / 8