第四章平行四边形（含答案）

中小学教育资源及组卷应用平台
第四章平行四边形
一、单选题
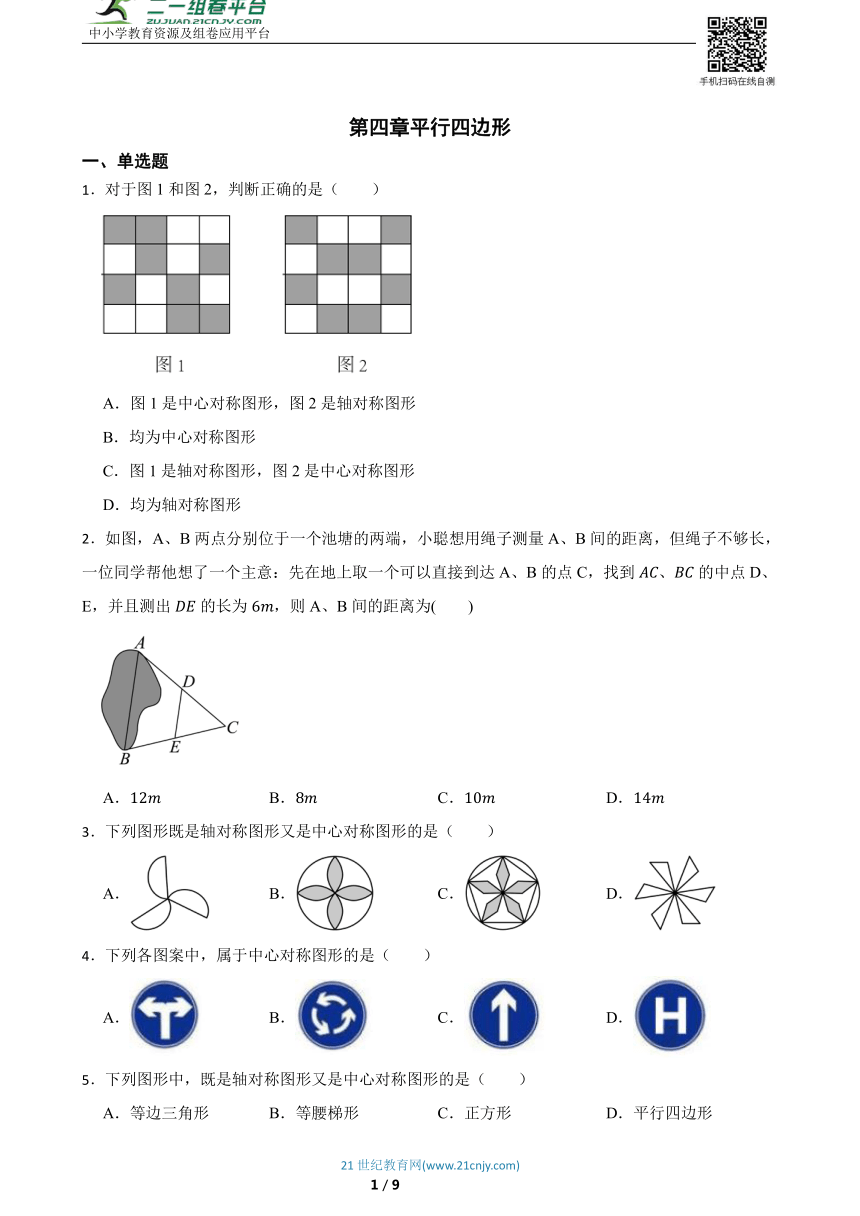
1．对于图1和图2，判断正确的是（　　）
A．图1是中心对称图形，图2是轴对称图形
B．均为中心对称图形
C．图1是轴对称图形，图2是中心对称图形
D．均为轴对称图形
2．如图，A、B两点分别位于一个池塘的两端，小聪想用绳子测量A、B间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A、B的点C，找到、的中点D、E，并且测出的长为，则A、B间的距离为(　　)
A． B． C． D．
3．下列图形既是轴对称图形又是中心对称图形的是（　　）
A． B． C． D．
4．下列各图案中，属于中心对称图形的是（　　）
A． B． C． D．
5．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A．等边三角形 B．等腰梯形 C．正方形 D．平行四边形
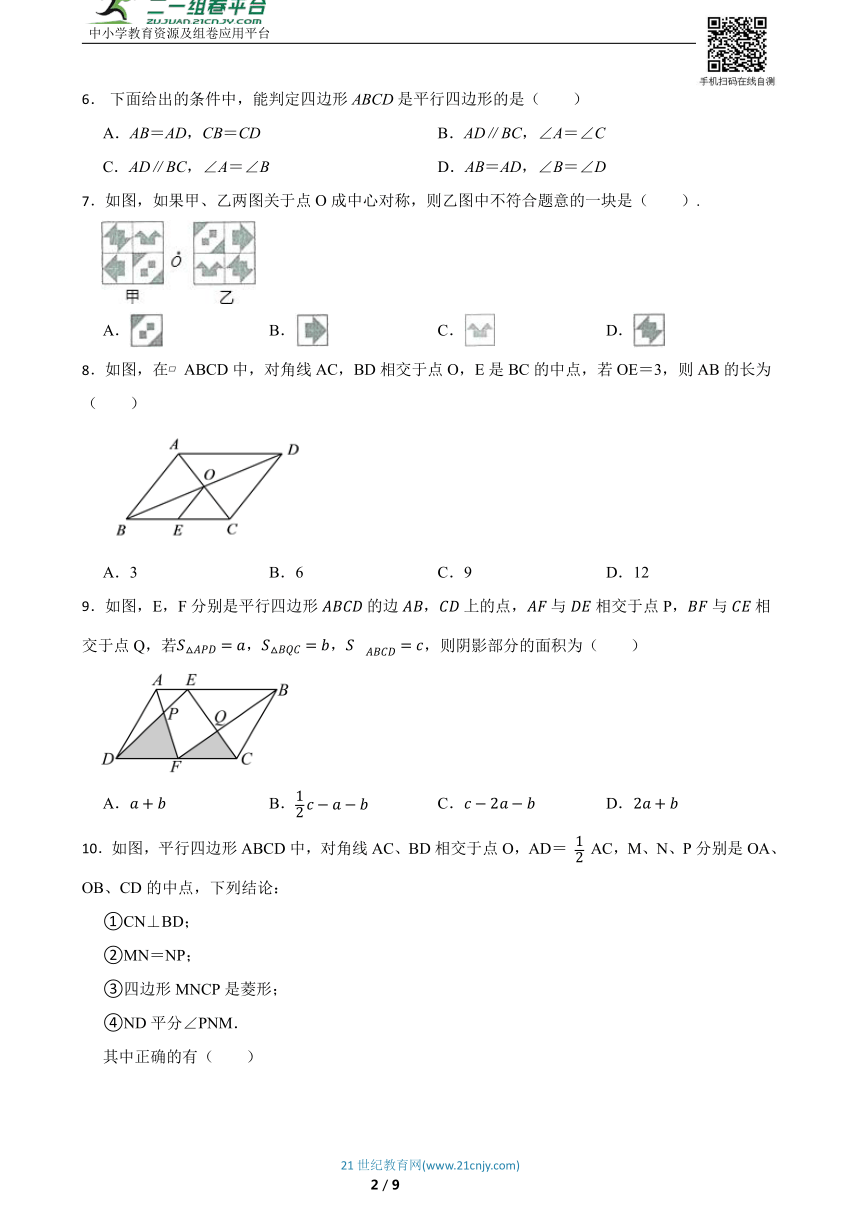
6． 下面给出的条件中，能判定四边形ABCD是平行四边形的是（　　）
A．AB＝AD，CB＝CD B．AD∥BC，∠A＝∠C
C．AD∥BC，∠A＝∠B D．AB＝AD，∠B＝∠D
7．如图，如果甲、乙两图关于点O成中心对称，则乙图中不符合题意的一块是（　　）.
A． B． C． D．
8．如图，在 ABCD中，对角线AC，BD相交于点O，E是BC的中点，若OE＝3，则AB的长为（　　）
A．3 B．6 C．9 D．12
9．如图，E，F分别是平行四边形的边，上的点，与相交于点P，与相交于点Q，若，则阴影部分的面积为（　　）
A． B． C． D．
10．如图，平行四边形ABCD中，对角线AC、BD相交于点O，AD＝ AC，M、N、P分别是OA、OB、CD的中点，下列结论：
①CN⊥BD；
②MN＝NP；
③四边形MNCP是菱形；
④ND平分∠PNM．
其中正确的有（　　）
A．1 个 B．2 个 C．3 个 D．4 个
二、填空题
11．已知一个多边形的每一个内角都相等，且每个内角都等于与它相邻的外角的9倍，则这个多边形的边数为　 　．
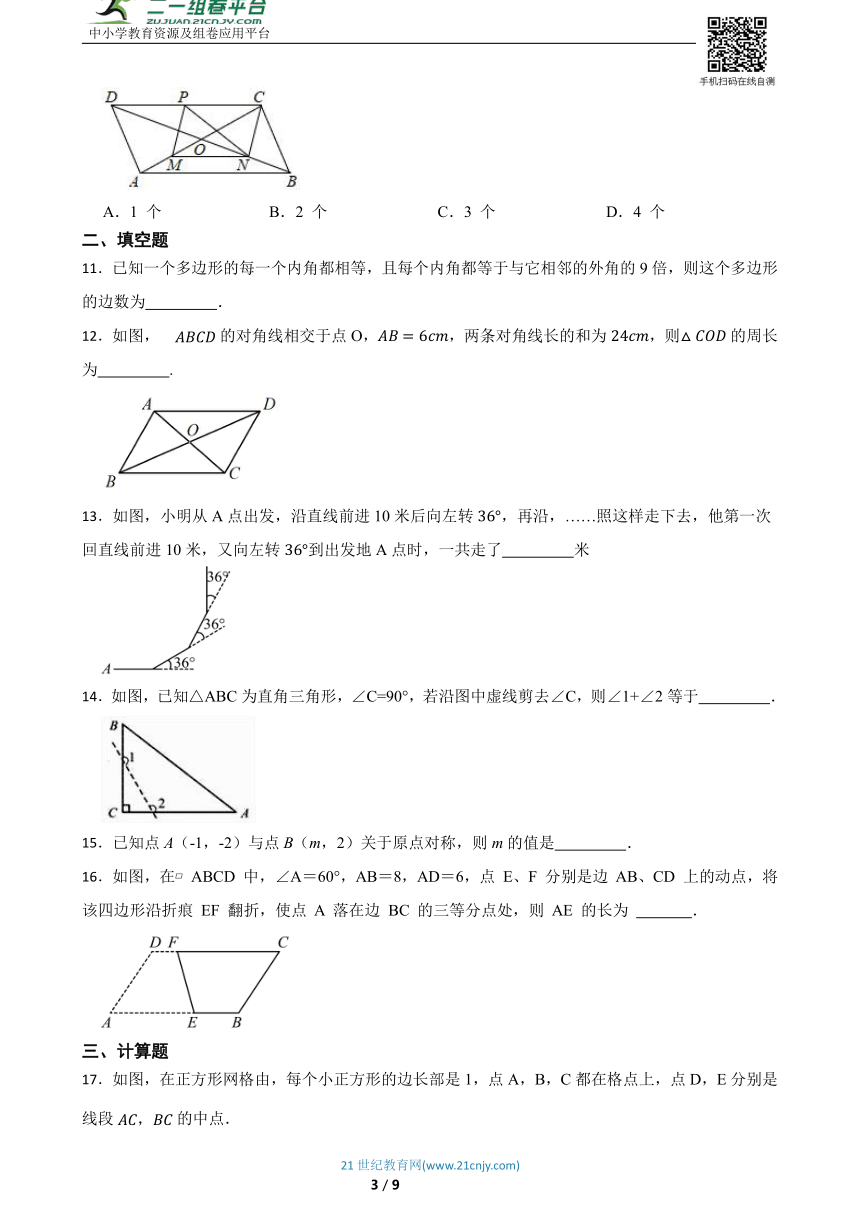
12．如图，的对角线相交于点O，，两条对角线长的和为，则的周长为　 　.
13．如图，小明从A点出发，沿直线前进10米后向左转，再沿，……照这样走下去，他第一次回直线前进10米，又向左转到出发地A点时，一共走了　 　米
14．如图，已知△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于　 　．
15．已知点A（-1，-2）与点B（m，2）关于原点对称，则m的值是　 　．
16．如图，在 ABCD 中，∠A＝60°，AB＝8，AD＝6，点 E、F 分别是边 AB、CD 上的动点，将该四边形沿折痕 EF 翻折，使点 A 落在边 BC 的三等分点处，则 AE 的长为 ．
三、计算题
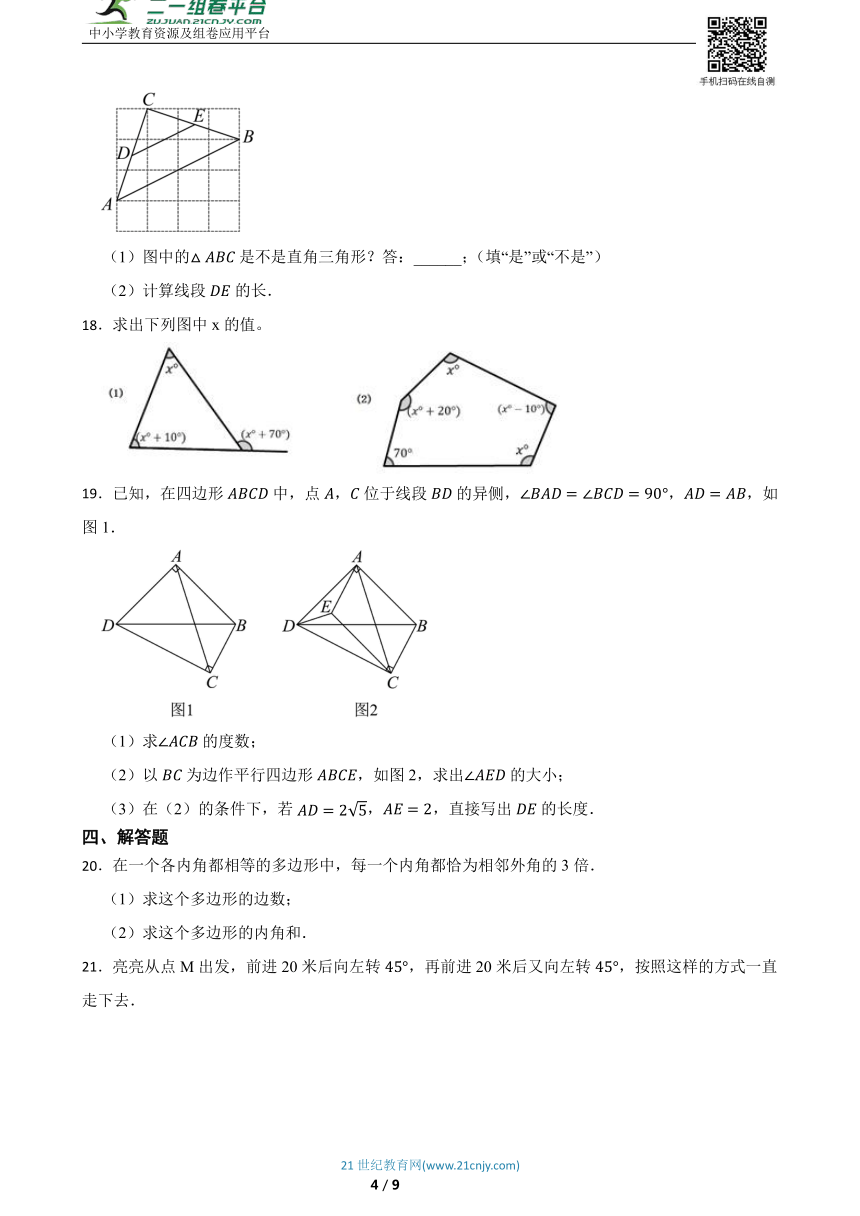
17．如图，在正方形网格由，每个小正方形的边长部是1，点A，B，C都在格点上，点D，E分别是线段的中点．
（1）图中的是不是直角三角形？答：______；（填“是”或“不是”）
（2）计算线段的长．
18．求出下列图中x的值。
19．已知，在四边形中，点，位于线段的异侧，，，如图1．
（1）求的度数；
（2）以为边作平行四边形，如图2，求出的大小；
（3）在（2）的条件下，若，，直接写出的长度．
四、解答题
20．在一个各内角都相等的多边形中，每一个内角都恰为相邻外角的3倍．
（1）求这个多边形的边数；
（2）求这个多边形的内角和．
21．亮亮从点M出发，前进20米后向左转，再前进20米后又向左转，按照这样的方式一直走下去．
（1）亮亮______（填“能”或“不能”）回到M点；
（2）亮亮走过的路线围成了______；（填详细图形名称）
（3）求（2）中图形的周长．
22．一个n边形的内角和比外角和多360度，求它的边数n．
23．如图，为等边三角形，在、上分别取点、，使，连接．
（1）求证：是等边三角形．
（2）点、分别是、的中点，连接，当绕点旋转到如图的位置时，求的度数．
（3）在(2)条件下，若，，，求的长．
答案解析部分
1．【答案】A
【知识点】轴对称图形；中心对称及中心对称图形
2．【答案】A
【知识点】三角形的中位线定理
3．【答案】B
【知识点】轴对称图形；中心对称及中心对称图形
4．【答案】D
【知识点】中心对称及中心对称图形
5．【答案】C
【知识点】轴对称图形；中心对称及中心对称图形
6．【答案】B
【知识点】平行四边形的判定
7．【答案】C
【知识点】中心对称及中心对称图形
8．【答案】B
【知识点】平行四边形的性质；三角形的中位线定理
9．【答案】B
【知识点】平行四边形的性质
10．【答案】C
【知识点】平行线的性质；平行四边形的性质；三角形的中位线定理
11．【答案】20
【知识点】一元一次方程的其他应用；多边形内角与外角
12．【答案】
【知识点】平行四边形的性质
13．【答案】100
【知识点】多边形内角与外角
14．【答案】270°
【知识点】三角形内角和定理；多边形内角与外角
15．【答案】1
【知识点】关于原点对称的点的坐标特征
16．【答案】或
【知识点】平行四边形的性质
17．【答案】（1）是
（2）
【知识点】最简二次根式；勾股定理；勾股定理的逆定理；三角形的中位线定理
18．【答案】（1）解：根据三角形外角的性质可得： ，
解得： ；
（2）解：根据五边形的内角和是 可得： ，
解得： .
【知识点】三角形的外角性质；多边形内角与外角
19．【答案】（1）
（2）
（3）
【知识点】等腰三角形的判定与性质；勾股定理；平行四边形的性质；三角形全等的判定-SAS
20．【答案】（1）解：设多边形的一个外角为，则与其相邻的内角等于，
由题意得，，
解得．
即多边形的每个外角为．
又多边形的外角和为，
∴多边形的外角个数为．
∴多边形的边数为8；
（2）解：这个多边形的内角和为．
【知识点】多边形内角与外角
21．【答案】（1）能
（2）正八边形
（3）（2）中图形的周长为160米
【知识点】多边形内角与外角
22．【答案】解：由多边形内角和公式，可得：
则此多边形的边数为：6
【知识点】多边形内角与外角
23．【答案】（1）证明：是等边三角形，
，
又，
是等边三角形；
（2）解：是等边三角形
，
，
≌
，
点、分别是、的中点，
．
，
≌，
，，
，
；
（3）解：如图，作EF⊥AB于点F，
∵，，
∴，，
∴，
点M是BE的中点，作MH⊥AB于点H，
∴，，
取AB中点P，连接MP，
则，，
∴，
∴，
∴，
在中，．
∴．
【知识点】等边三角形的判定与性质；含30°角的直角三角形；三角形全等的判定-SAS；三角形的中位线定理
21世纪教育网(www.21cnjy.com)
9 / 9