5.1矩形（含答案）

中小学教育资源及组卷应用平台
5.1矩形
一、填空题
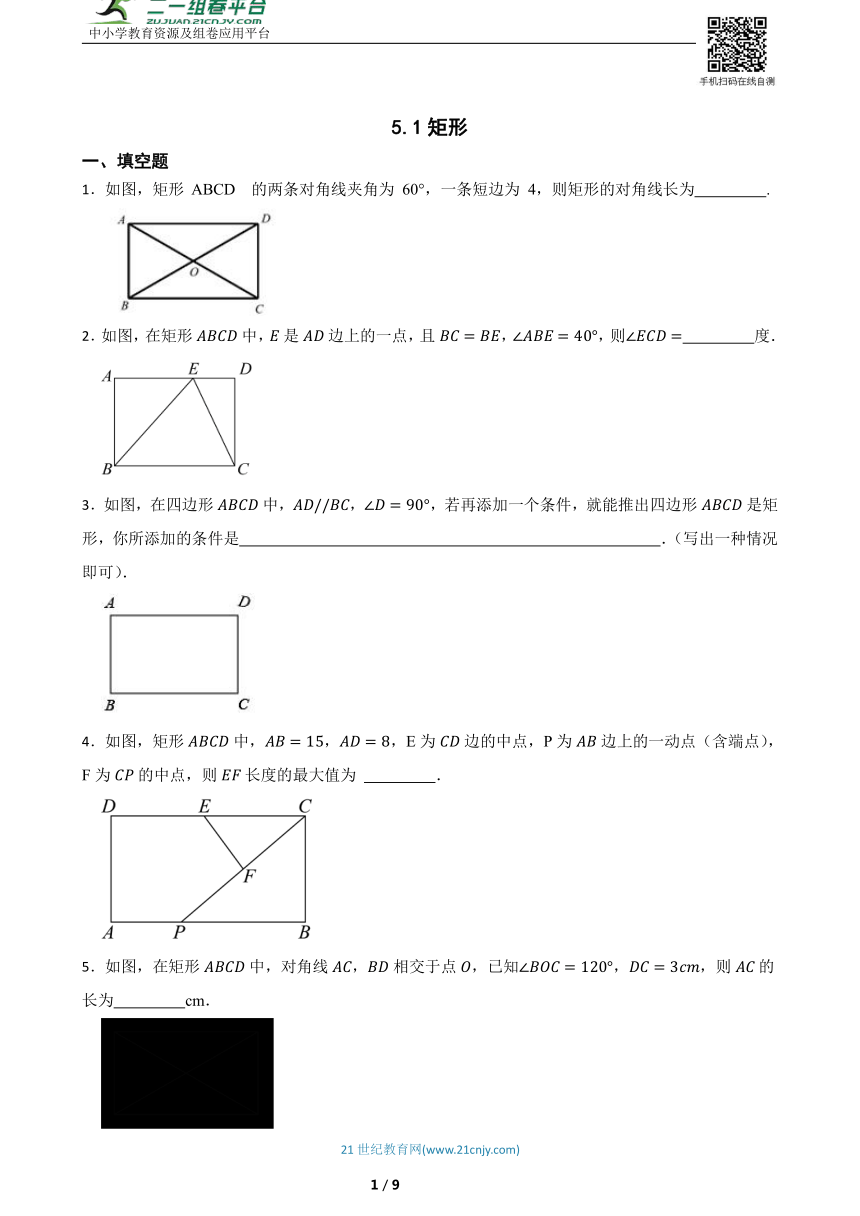
1．如图，矩形 ABCD 的两条对角线夹角为 60°，一条短边为 4，则矩形的对角线长为　 　.
2．如图，在矩形中，是边上的一点，且，，则　 　度．
3．如图，在四边形中，，，若再添加一个条件，就能推出四边形是矩形，你所添加的条件是　 　．（写出一种情况即可）．
4．如图，矩形中，，，E为边的中点，P为边上的一动点（含端点），F为的中点，则长度的最大值为 　 　．
5．如图，在矩形中，对角线，相交于点，已知，，则的长为　 　cm．
6．在平行四边形 中，若再增加一个条件　 　，使平行四边形 能成为矩形（填写一个你认为正确的即可）．
二、单选题
7．如图，将矩形沿折叠，使顶点C恰好落在边的中点上，若，折痕为，则的长为（　　）
A．5 B．4 C．3 D．
8．如图，四边形是矩形，点E在线段的延长线上，连接交于点F，，G是的中点，若，那么的长为（　　）
A． B． C．5 D．3
9．如图，矩形ABCD的对角线AC，BD相交于点O，AB＝2，∠ABO＝60°，线段EF绕点O转动，与AD，BC分别相交于点E，F，当∠AOE＝60°时，EF的长为（　　）.
A．1 B． C．2 D．4
10．如图，矩形对角线相交于点O，，，则的为（　　）
A．4 B．8 C． D．10
11．如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，AE=3，ED=3BE，则AB的值为（　　）
A．6 B．5 C． D．
三、计算题
12．如图，点是矩形的对称中心，点，点分别位于，上，且经过点，，，，点在上运动，点，在上运动，且则：
（1）周长的最小值是　 　．
（2）四边形周长的最小值是　 　．
13．如图，在矩形中，对角线，相交于点，，，点在线段上，从点至点运动，连接，以为边作等边，点和点分别位于两侧．
（1）当点运动到点时，求的长；
（2）点在线段上从点至点运动过程中，求的最小值．
14．课本再现：
（1）如图，在矩形中，，，是上不与和重合的一个动点，过点分别作和的垂线，垂足分别为，．求的值．
如图1，连接，利用与的面积之和是矩形面积的，可求出的值，请你写出求解过程；
知识应用：
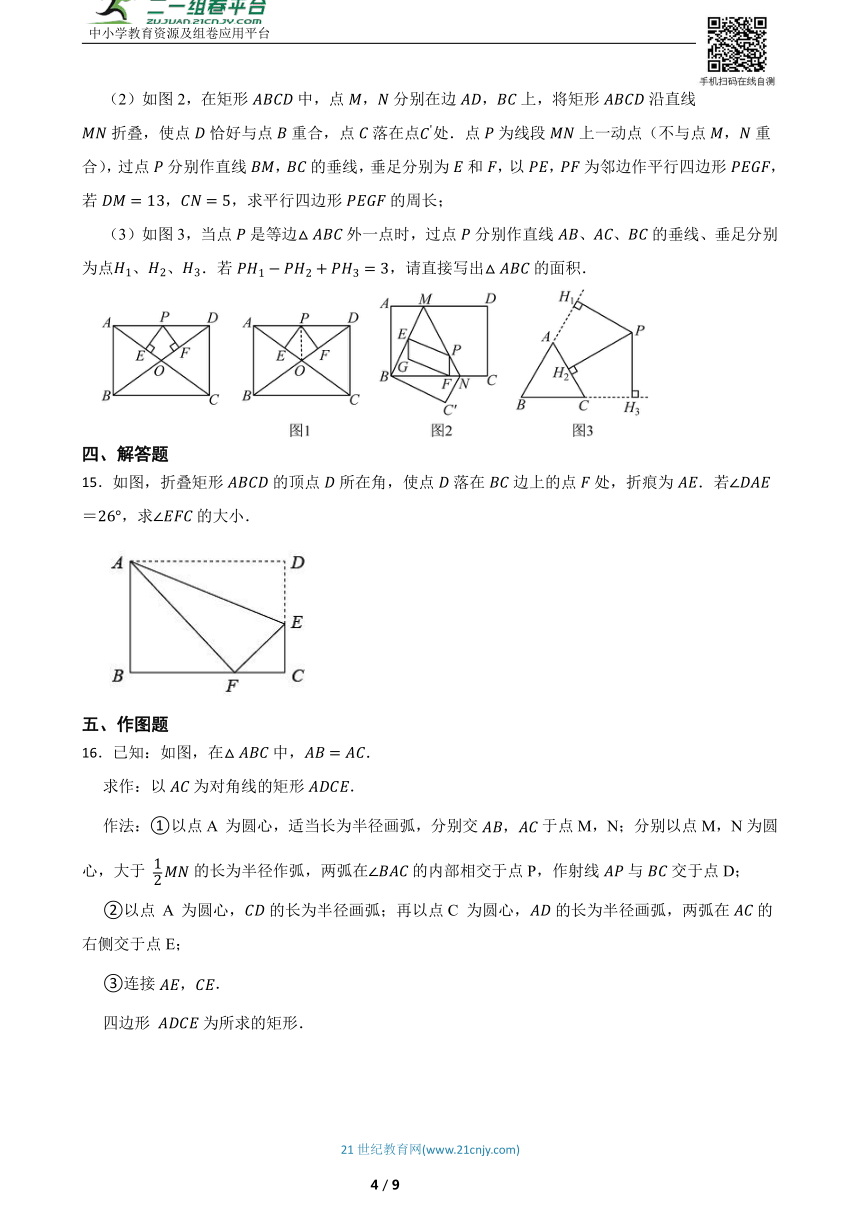
（2）如图2，在矩形中，点，分别在边，上，将矩形沿直线折叠，使点恰好与点重合，点落在点处．点为线段上一动点（不与点，重合），过点分别作直线，的垂线，垂足分别为和，以，为邻边作平行四边形，若，，求平行四边形的周长；
（3）如图3，当点是等边外一点时，过点分别作直线、、的垂线、垂足分别为点、、．若，请直接写出的面积．
四、解答题
15．如图，折叠矩形的顶点所在角，使点落在边上的点处，折痕为．若＝，求的大小．
五、作图题
16．已知：如图，在中，．
求作：以为对角线的矩形．
作法：①以点A 为圆心，适当长为半径画弧，分别交于点M，N；分别以点M，N为圆心，大于 的长为半径作弧，两弧在的内部相交于点P，作射线与交于点D；
②以点 A 为圆心，的长为半径画弧；再以点C 为圆心，的长为半径画弧，两弧在的右侧交于点E；
③连接．
四边形 为所求的矩形．
（1）根据以上作法，使用直尺和圆规补全图形(保留作图痕迹)；
（2）完成以下证明．
证明：∵，
∴四边形为平行四边形( )．(填推理的依据)
由作图可知，平分，
又∵，
∴ ( )．(填推理的依据)
∴．
∴平行四边形是矩形( )．(填推理的依据)
六、综合题
17．如图， ABCD的对角线AC、BD相交于点O，AE=CF．
（1）求证：△BOE≌△DOF；
（2）若BD=EF，连接DE、BF，判断四边形EBFD的形状，无需说明理由.
18．如图，已知点M(－2，0)点N(0，6)，A为线段MN上一点，AB⊥ 轴，垂足为B，AC⊥ 轴，垂足为点C．
（1）求直线MN的函数表达式；
（2）若点A的横坐标为－1，求矩形ABOC的面积．
19．如图，在平行四边形中，过点作于点，点在边上，且，连接，．
（1）求证：四边形是矩形；
（2）若平分，，，求的长．
答案解析部分
1．【答案】8
【知识点】等边三角形的判定与性质；矩形的性质
2．【答案】
【知识点】等腰三角形的性质；矩形的性质
3．【答案】或或（写出一种情况即可）
【知识点】矩形的判定
4．【答案】
【知识点】勾股定理；矩形的性质；三角形的中位线定理
5．【答案】6cm
【知识点】含30°角的直角三角形；矩形的性质
6．【答案】 或
【知识点】矩形的判定
7．【答案】A
【知识点】勾股定理；矩形的性质
8．【答案】B
【知识点】勾股定理；矩形的性质；直角三角形斜边上的中线
9．【答案】C
【知识点】等边三角形的判定与性质；矩形的判定与性质
10．【答案】B
【知识点】等边三角形的判定与性质；矩形的性质
11．【答案】C
【知识点】矩形的性质
12．【答案】；
【知识点】两点之间线段最短；勾股定理；矩形的性质
13．【答案】（1）2
（2）
【知识点】等边三角形的判定与性质；勾股定理；矩形的性质；三角形全等的判定-SAS
14．【答案】（1）；（2）24；（3）
【知识点】勾股定理；矩形的性质
15．【答案】
【知识点】矩形的性质
16．【答案】（1）解：如图所示，四边形ADCE即为所求；
（2）证明：∵，
∴四边形为平行四边形 (两组对边分别相等的四边形是平行四边形)，
由作图可知，平分，
又∵，
∴ (等腰三角形”三线合一“)．
∴，
∴平行四边形是矩形(有一个角是直角的平行四边形是矩形)，
故答案为：两组对边分别相等的四边形是平行四边形，等腰三角形”三线合一“，有一个角是直角的平行四边形是矩形.
【知识点】矩形的判定；尺规作图-作角的平分线；等腰三角形的性质-三线合一
17．【答案】（1）证明：∵四边形ABCD是平行四边形，
∴OA=OC，OB=OD，
∵AE=CF，∴OE=OF，
在△BOE和△DOF中，
，
∴△BOE≌△DOF（SAS）.
（2）解：四边形EBFD是矩形；
理由如下：
∵OB=OD，OE=OF，∴四边形EBFD是平行四边形，∵BD=EF，∴四边形EBFD是矩形．
【知识点】全等三角形的判定与性质；平行四边形的性质；矩形的判定
18．【答案】（1）设直线MN的表达式为 ，
把M，N坐标代入直线解析式，得，
解得
直线MN函数表达式为：
（2）把 代入 ，得 ，
点A坐标为( ，3)
AB=3，AC=1，
矩形ABOC的面积S=1×3=3
【知识点】待定系数法求一次函数解析式；矩形的性质
19．【答案】（1）证明：四边形是平行四边形，
，．
，，
，
四边形是平行四边形．
又，即，
平行四边形是矩形．
（2）解：平分，．
，，
，．
在中，由勾股定理，得．
由（1）知，四边形DEBF是矩形，
【知识点】平行四边形的性质；矩形的判定
21世纪教育网(www.21cnjy.com)
1 / 9