5.3正方形（含答案）

中小学教育资源及组卷应用平台
5.3正方形
一、填空题
1．正方形 的对角线长为 ，面积为　 　.
2．如图，点A，B，E在同一条直线上，正方形，正方形的边长分别为6，8，H为线段的中点，则的长为 　 　．
3．如图1，有甲，乙两种大小不同的正方形纸片，把正方形甲放置在正方形乙中，连结，，得到图2，再将图2这样的四个图案不重叠，无缝隙地拼成如图3所示的正方形，若正方形中阴影区域面积和为12，且，则一张正方形甲和一 张正方形乙的面积和为 　 　．
4．在正方形ABCD中，对角线AC＝2cm，那么正方形ABCD的面积为．
5．如图，菱形ABCD中，∠B＝60°，AB＝3，四边形ACEF是正方形，则EF的长为　 　．
6．面积为 的正方形的边长是　 　．
二、单选题
7．如图，已知正方形的边长为4，点M在上，，点N是上的一个动点，那么的最小值是（　　）
A．3 B．4 C．5 D．6
8．下列命题中正确的是（　　）
A．一组对边平行，另一组对边相等的四边形是平行四边形
B．对角线相等的四边形是矩形
C．对角线相互平分且垂直的四边形是菱形
D．对角线相等且相互垂直的四边形是正方形
9．已知四边形对角线，相交于点O，下列结论正确的是（　　）．
A．，
B．当，时，四边形是菱形
C．若四边形是矩形，则
D．当且时，四边形是正方形
10．下列说法正确的是（　　）
A．菱形都是相似图形
B．矩形都是相似图形
C．对角线相等的菱形是正方形
D．对角线互相垂直的四边形是菱形
11．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是（　　）
A． B． C． D．2
三、解答题
12．已知：如图，正方形，连接，E是延长线上一点，，连接交于点F．
（1）求的度数；
（2）若，求点F到的距离．
四、计算题
13．如图，在边长为4的正方形中，点是边上一点，，连结，以为斜边作等腰，点在正方形内，连接；
（1）①_________；
②_________；
（2）求的长．
14．在平面直角坐标系中，四边形为正方形，，，为线段上一点，．
（1）求直线的函数解析式；
（2）在正方形的边上有一点，若，求点坐标；
（3）作点关于轴的对称点，点为直线上一动点，在射线上是否存在点，使为等腰直角三角形，若存在，请直接写出点坐标，若不存在，请说明理由．
15．如图，在平面直角坐标系中，直线与x轴、y轴分别交于点D、C，直线与y轴交于点，与直线交于点．
（1）求直线的解析式；
（2）点E是射线上一动点，过点E作轴，交直线于点F．若以O、C、E、F为顶点的四边形是平行四边形，请求出点E的坐标；
（3）设P是射线上一点，在平面内是否存在点Q，使以B、C、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
五、作图题
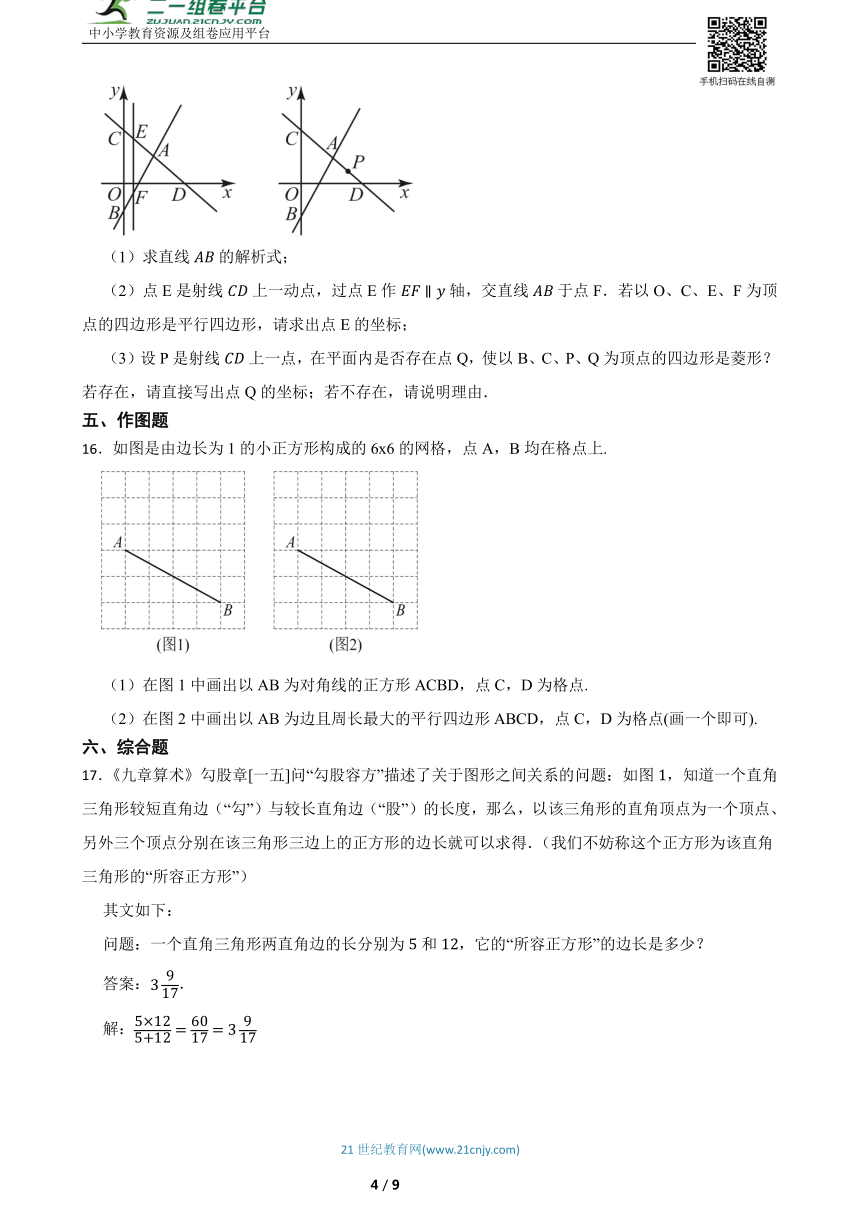
16．如图是由边长为1的小正方形构成的6x6的网格，点A，B均在格点上.
（1）在图1中画出以AB为对角线的正方形ACBD，点C，D为格点.
（2）在图2中画出以AB为边且周长最大的平行四边形ABCD，点C，D为格点(画一个即可).
六、综合题
17．《九章算术》勾股章[一五]问“勾股容方”描述了关于图形之间关系的问题：如图，知道一个直角三角形较短直角边（“勾”）与较长直角边（“股”）的长度，那么，以该三角形的直角顶点为一个顶点、另外三个顶点分别在该三角形三边上的正方形的边长就可以求得．（我们不妨称这个正方形为该直角三角形的“所容正方形”）
其文如下：
问题：一个直角三角形两直角边的长分别为和，它的“所容正方形”的边长是多少？
答案：．
解：
（1）已知：如图，在中，，若，，求“所容正方形”的边长．
（2）应用（1）中的结论解决问题：如图，中山公园有一块菱形场地，其面积为，两条对角线长度之和为．现要在这个菱形场地上修建一个正方形花圃，并且要使正方形花圃的四个顶点分别落在菱形场地的四条边上，则该正方形花圃的边长为多少？
18．如图，有一张边长为 的正方形纸板，现将该纸板的四个角剪掉，制作一个有底无盖的长方体盒子，剪掉的四个角是面积相等的小正方形，此小正方形的边长为3 .求：
（1）剪掉四个角后，制作长方体盒子的纸板的面积；
（2）长方体盒子的体积.
19．如图，在四边形AECF中， ．CE、CF分别是△ABC的内，外角平分线．
（1）求证：四边形AECF是矩形．
（2）当△ABC满足什么条件时，四边形AECF是正方形？请说明理由．
七、实践探究题
20．【问题背景】
如图，是一张等腰直角三角形纸板，，取、、中点进行第次剪取，记所得正方形面积为，如图，在余下的和中，分别剪取正方形，得到两个相同的正方形，称为第次剪取，并记这两个正方形面积和为如图.
【问题探究】
（1） ______ ；
（2）如图，再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第次剪取，并记这四个正方形面积和为继续操作下去，则第次剪取时， ______ ；第次剪取时， ______ ．
【拓展延伸】
在第次剪取后，余下的所有小三角形的面积之和为______ ．
答案解析部分
1．【答案】1
【知识点】正方形的性质
2．【答案】
【知识点】勾股定理；正方形的性质；直角三角形斜边上的中线
3．【答案】
【知识点】正方形的性质
4．【答案】2
【知识点】正方形的性质
5．【答案】3
【知识点】菱形的性质；正方形的性质
6．【答案】
【知识点】正方形的性质
7．【答案】C
【知识点】勾股定理；正方形的性质
8．【答案】C
【知识点】菱形的判定；矩形的判定；正方形的判定；真命题与假命题
9．【答案】C
【知识点】菱形的判定；矩形的性质；正方形的判定
10．【答案】C
【知识点】菱形的判定；矩形的性质；正方形的判定
11．【答案】A
【知识点】勾股定理；正方形的性质；直角三角形斜边上的中线
12．【答案】（1）
（2）2
【知识点】角平分线的性质；等腰三角形的性质；正方形的性质
13．【答案】（1）①45°②3
（2）
【知识点】等腰三角形的性质；勾股定理；正方形的性质
14．【答案】（1）
（2）或
（3）存在，或或或
【知识点】待定系数法求一次函数解析式；正方形的性质；一次函数的实际应用-几何问题
15．【答案】（1）
（2）或
（3）或或
【知识点】待定系数法求一次函数解析式；平行四边形的性质；菱形的判定与性质；正方形的判定与性质
16．【答案】（1）
（2）
【知识点】平行四边形的性质；正方形的性质
17．【答案】（1）正方形边长为；
（2）该正方形花圃的边长为．
【知识点】菱形的性质；正方形的判定与性质
18．【答案】（1）解：制作长方体盒子的纸板的面积为：
（ ）
（2）解：长方体盒子的体积：
（ ）
【知识点】正方形的性质
19．【答案】（1）证明：∵CE、CF分别是 的内、外角平分线，
， ．
，即 ．
，
∴四边形AECF是矩形．
（2）解：当 满足 时，四边形AECF是正方形．
理由：
． ．
∵四边形AECF是矩形，∴四边形AECF是正方形．
【知识点】矩形的判定与性质；正方形的判定；角平分线的判定
20．【答案】（1）；（2），；【拓展延伸】
【知识点】勾股定理；正方形的性质
21世纪教育网(www.21cnjy.com)
1 / 9