第五章特殊平行四边形【培优】(含答案)
文档属性
| 名称 | 第五章特殊平行四边形【培优】(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 472.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-26 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第五章特殊平行四边形【培优】
一、填空题
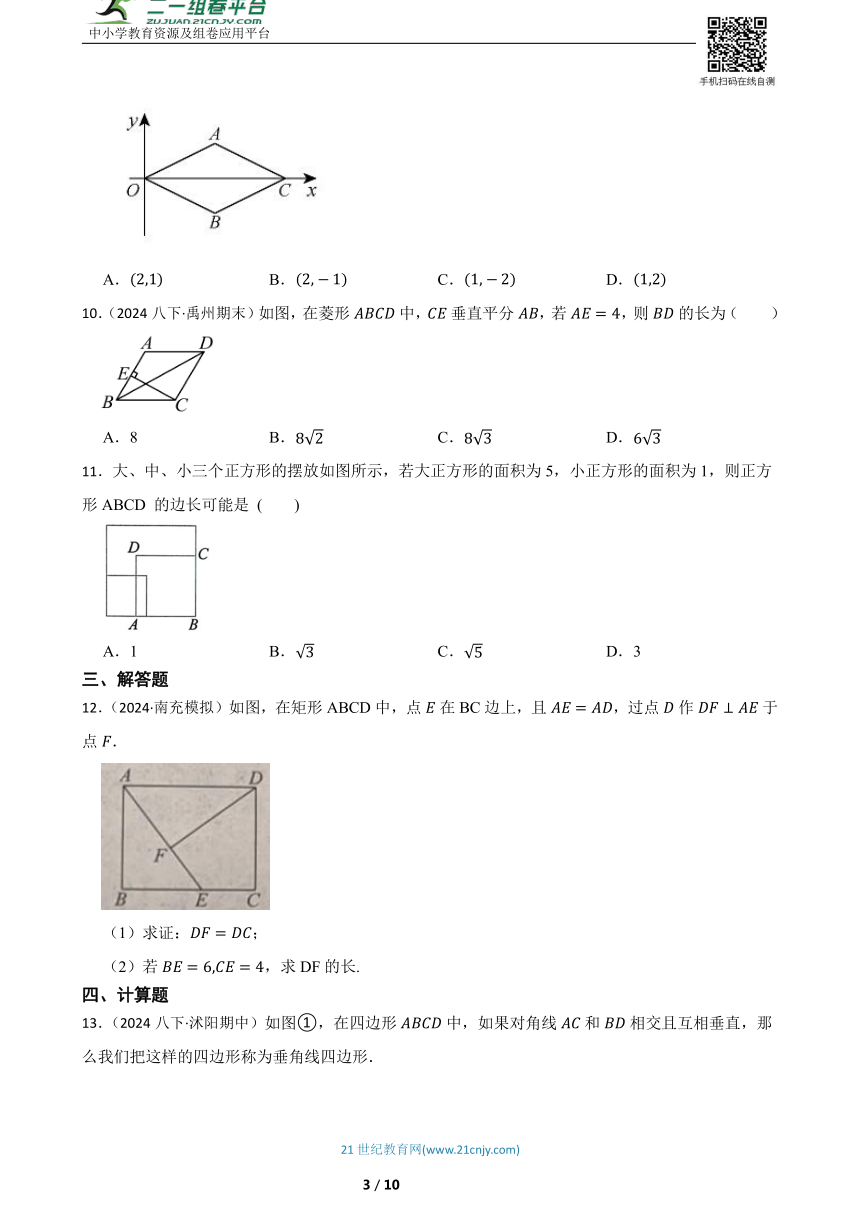
1.(2024八下·晋安期中)如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为 .
2.(2024八下·巴南月考)如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
3.(2023八下·栾城期末)如图,在矩形中,对角线相交于点O,的度数为 .
4.(2023八下·冷水滩月考)如图,在正方形中,P,Q分别为的中点,若,则大小为 .
5.(2024八下·西安期末)如图,矩形中,,,点P从B点沿向D点移动,若过点P作的垂线交于E点,过点P作的垂线交于F点,则的长度最小为 .
6.(2024八下·昌平期中)如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段,,,的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:
①存在无数个中点四边形是平行四边形;②存在无数个中点四边形是菱形;③存在无数个中点四边形是矩形;④存在两个中点四边形是正方形.所有正确结论的序号是 .
二、单选题
7.(2024九下·广阳模拟)如图,在四边形中,,,,,E、F是上的两动点,且,点E从点B出发,当点F移动到点C时,两点停止运动.在四边形形状的变化过程中,依次出现的特殊四边形是( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→菱形→正方形→平行四边形
C.平行四边形→菱形→正方形→菱形
D.平行四边形→矩形→菱形→平行四边形
8.(2024八下·诸暨期末)以下说法正确的是( )
A.菱形的对角线互相垂直且相等
B.矩形的对角线互相平分且互相垂直
C.正方形的对角线互相垂直且平分
D.平行四边形的对角线互相平分且相等
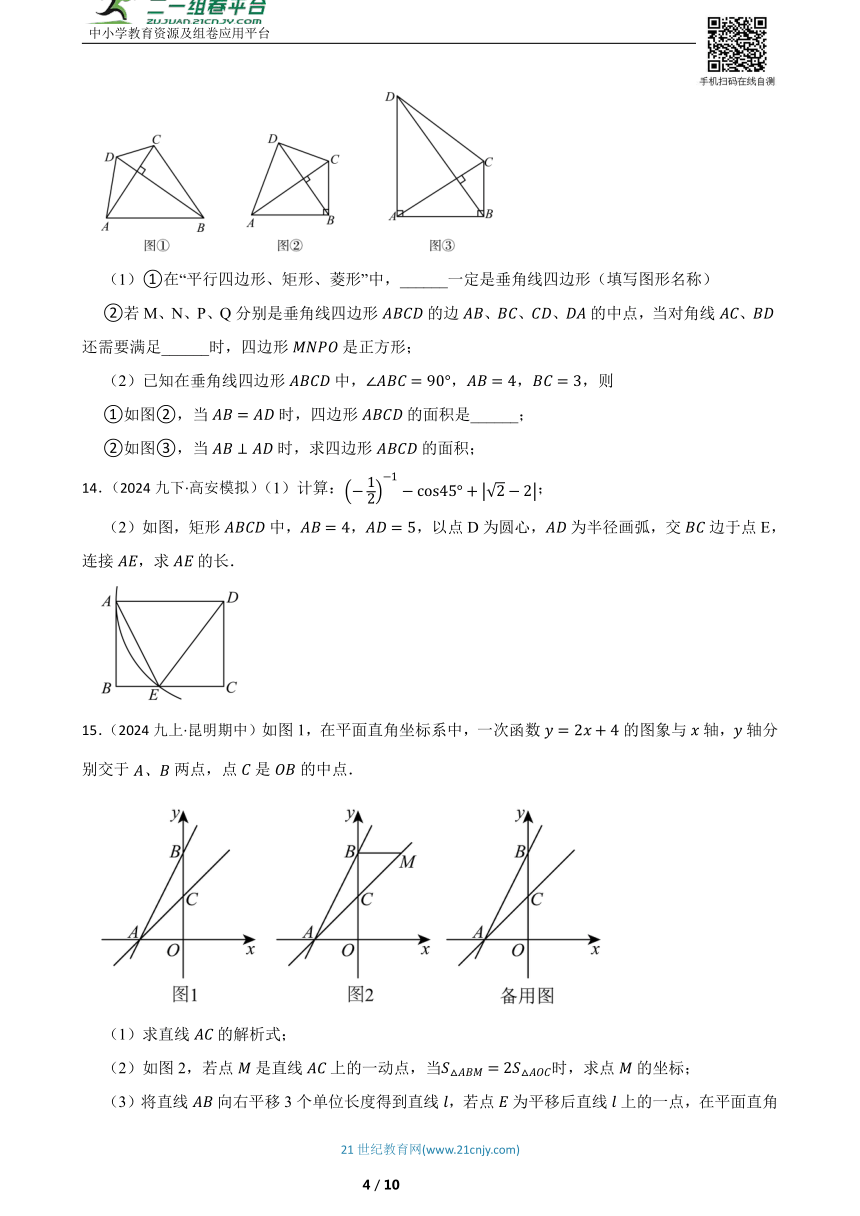
9.(2024八上·东城期中)菱形在平面直角坐标系中的位置如图所示,若点的坐标是,点的纵坐标是则点的坐标是( )
A. B. C. D.
10.(2024八下·禹州期末)如图,在菱形中,垂直平分,若,则的长为( )
A.8 B. C. D.
11.大、中、小三个正方形的摆放如图所示,若大正方形的面积为5,小正方形的面积为1,则正方形ABCD 的边长可能是 ( )
A.1 B. C. D.3
三、解答题
12.(2024·南充模拟)如图,在矩形ABCD中,点在BC边上,且,过点作于点.
(1)求证:;
(2)若,求DF的长.
四、计算题
13.(2024八下·沭阳期中)如图①,在四边形中,如果对角线和相交且互相垂直,那么我们把这样的四边形称为垂角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是垂角线四边形(填写图形名称)
②若M、N、P、Q分别是垂角线四边形的边、、、的中点,当对角线、还需要满足______时,四边形是正方形;
(2)已知在垂角线四边形中,,,,则
①如图②,当时,四边形的面积是______;
②如图③,当时,求四边形的面积;
14.(2024九下·高安模拟)(1)计算:;
(2)如图,矩形中,,,以点D为圆心,为半径画弧,交边于点E,连接,求的长.
15.(2024九上·昆明期中)如图1,在平面直角坐标系中,一次函数的图象与轴,轴分别交于两点,点是的中点.
(1)求直线的解析式;
(2)如图2,若点是直线上的一动点,当时,求点的坐标;
(3)将直线向右平移3个单位长度得到直线,若点为平移后直线上的一点,在平面直角坐标系中是否存在点,使以点为顶点,为边的四边形为菱形,若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
五、作图题
16.(2023八下·苏州工业园期末)如图,已知矩形.
(1)用直尺和圆规分别在、边上找点E、F,使得四边形是菱形;(保留作图痕迹,不写作法,并给出证明.)
(2)若,,求菱形的周长.
六、综合题
17.(2024九下·合肥期中)如图是某物理兴趣小组利用矩形模块设计的一个感光元件,平行光线从区域射入,线段为感光区域,已知,,,,则感光区域的长度之和为多少?(结果精确到,参考数据:,,,)
18.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
19.(2024八下·宜城期中)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
七、实践探究题
20.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】
【知识点】勾股定理;矩形的判定与性质;轴对称的性质
2.【答案】
【知识点】等边三角形的判定与性质;含30°角的直角三角形;矩形的性质
3.【答案】
【知识点】三角形的外角性质;矩形的性质
4.【答案】
【知识点】等腰三角形的性质;正方形的性质;三角形全等的判定-SAS
5.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质
6.【答案】①②③④
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
7.【答案】A
【知识点】平行四边形的判定;菱形的判定;矩形的判定
8.【答案】C
【知识点】平行四边形的性质;菱形的性质;矩形的性质;正方形的性质
9.【答案】B
【知识点】坐标与图形性质;菱形的性质
10.【答案】C
【知识点】线段垂直平分线的性质;等边三角形的判定与性质;勾股定理;菱形的性质
11.【答案】B
【知识点】无理数的估值;正方形的性质
12.【答案】(1)证明:,
在和中,
(2)解:
【知识点】三角形全等及其性质;勾股定理;矩形的性质;三角形全等的判定-AAS
13.【答案】(1)①菱形;②
(2)①12;②
【知识点】勾股定理;菱形的性质;三角形全等的判定-SAS;三角形的中位线定理
14.【答案】(1);(2)
【知识点】负整数指数幂;勾股定理;矩形的性质;求特殊角的三角函数值
15.【答案】(1)
(2)或
(3)点F的坐标为
【知识点】待定系数法求一次函数解析式;勾股定理;菱形的性质;一次函数图象的平移变换
16.【答案】(1)解:连接,利用直尺和圆规作线段的垂直平分线交,于点E,F,则点E,F为所求.如图,
证明如下:设与交于点O,
∵四边形为矩形,
∴,,
∴,
∵是的垂直平分线,
∴,,,
在和中,
,
∴,
∴,
∴,
∴四边形为菱形,
∴点E,F为所求作的点.
(2)解:设菱形的边长为x,则菱形的的周长为,
在中,,,,
由勾股定理得:,
即:,
解得:,
∴菱形的的周长为.
答:菱形的周长为20.
【知识点】线段垂直平分线的性质;勾股定理;菱形的判定;矩形的性质;尺规作图-垂直平分线
17.【答案】
【知识点】平行线的性质;勾股定理;矩形的判定与性质;解直角三角形的其他实际应用
18.【答案】(1)解:∵ABCD是菱形,
∴AC⊥BD,
∴直角△OCD中,OC= (cm)
(2)解:∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB OC=4×3=12(cm2)
【知识点】菱形的性质;矩形的判定与性质
19.【答案】(1)解:BD=CD.
理由如下:依题意得AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD
(2)解:当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴ AFBD是矩形.
【知识点】全等三角形的判定与性质;矩形的判定
20.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
2 / 10
第五章特殊平行四边形【培优】
一、填空题
1.(2024八下·晋安期中)如图,矩形中,,是的中点,线段在边上左右滑动;若,则的最小值为 .
2.(2024八下·巴南月考)如图,矩形纸片的对角线,相交于点,,将矩形纸片翻折,使点恰好落在点处,折痕为,点在边上,则的长为 .
3.(2023八下·栾城期末)如图,在矩形中,对角线相交于点O,的度数为 .
4.(2023八下·冷水滩月考)如图,在正方形中,P,Q分别为的中点,若,则大小为 .
5.(2024八下·西安期末)如图,矩形中,,,点P从B点沿向D点移动,若过点P作的垂线交于E点,过点P作的垂线交于F点,则的长度最小为 .
6.(2024八下·昌平期中)如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段,,,的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:
①存在无数个中点四边形是平行四边形;②存在无数个中点四边形是菱形;③存在无数个中点四边形是矩形;④存在两个中点四边形是正方形.所有正确结论的序号是 .
二、单选题
7.(2024九下·广阳模拟)如图,在四边形中,,,,,E、F是上的两动点,且,点E从点B出发,当点F移动到点C时,两点停止运动.在四边形形状的变化过程中,依次出现的特殊四边形是( )
A.平行四边形→菱形→矩形→平行四边形
B.平行四边形→菱形→正方形→平行四边形
C.平行四边形→菱形→正方形→菱形
D.平行四边形→矩形→菱形→平行四边形
8.(2024八下·诸暨期末)以下说法正确的是( )
A.菱形的对角线互相垂直且相等
B.矩形的对角线互相平分且互相垂直
C.正方形的对角线互相垂直且平分
D.平行四边形的对角线互相平分且相等
9.(2024八上·东城期中)菱形在平面直角坐标系中的位置如图所示,若点的坐标是,点的纵坐标是则点的坐标是( )
A. B. C. D.
10.(2024八下·禹州期末)如图,在菱形中,垂直平分,若,则的长为( )
A.8 B. C. D.
11.大、中、小三个正方形的摆放如图所示,若大正方形的面积为5,小正方形的面积为1,则正方形ABCD 的边长可能是 ( )
A.1 B. C. D.3
三、解答题
12.(2024·南充模拟)如图,在矩形ABCD中,点在BC边上,且,过点作于点.
(1)求证:;
(2)若,求DF的长.
四、计算题
13.(2024八下·沭阳期中)如图①,在四边形中,如果对角线和相交且互相垂直,那么我们把这样的四边形称为垂角线四边形.
(1)①在“平行四边形、矩形、菱形”中,______一定是垂角线四边形(填写图形名称)
②若M、N、P、Q分别是垂角线四边形的边、、、的中点,当对角线、还需要满足______时,四边形是正方形;
(2)已知在垂角线四边形中,,,,则
①如图②,当时,四边形的面积是______;
②如图③,当时,求四边形的面积;
14.(2024九下·高安模拟)(1)计算:;
(2)如图,矩形中,,,以点D为圆心,为半径画弧,交边于点E,连接,求的长.
15.(2024九上·昆明期中)如图1,在平面直角坐标系中,一次函数的图象与轴,轴分别交于两点,点是的中点.
(1)求直线的解析式;
(2)如图2,若点是直线上的一动点,当时,求点的坐标;
(3)将直线向右平移3个单位长度得到直线,若点为平移后直线上的一点,在平面直角坐标系中是否存在点,使以点为顶点,为边的四边形为菱形,若存在,请直接写出所有满足条件的点的坐标;若不存在,请说明理由.
五、作图题
16.(2023八下·苏州工业园期末)如图,已知矩形.
(1)用直尺和圆规分别在、边上找点E、F,使得四边形是菱形;(保留作图痕迹,不写作法,并给出证明.)
(2)若,,求菱形的周长.
六、综合题
17.(2024九下·合肥期中)如图是某物理兴趣小组利用矩形模块设计的一个感光元件,平行光线从区域射入,线段为感光区域,已知,,,,则感光区域的长度之和为多少?(结果精确到,参考数据:,,,)
18.如图,O是菱形ABCD对角线AC与BD的交点,CD=5cm,OD=3cm;过点C作CE∥DB,过点B作BE∥AC,CE与BE相交于点E.
(1)求OC的长;
(2)求四边形OBEC的面积.
19.(2024八下·宜城期中)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)线段BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
七、实践探究题
20.小惠自编一题: “如图, 在四边形 中, 对角线 交于点 . 求证: 四边形 是菱形”,并将自己的证明过程与同学小洁交流.
小惠: 小洁:
证明: , 这个题目还缺少条件, 需要补充一个条件才 能证明.
垂直平分 .
,
四边形 是菱形.
若赞同小惠的证法,请在第一个方框内打 “ √ ”;若赞成小洁的说法, 请你补充一个条件, 并证明.
答案解析部分
1.【答案】
【知识点】勾股定理;矩形的判定与性质;轴对称的性质
2.【答案】
【知识点】等边三角形的判定与性质;含30°角的直角三角形;矩形的性质
3.【答案】
【知识点】三角形的外角性质;矩形的性质
4.【答案】
【知识点】等腰三角形的性质;正方形的性质;三角形全等的判定-SAS
5.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质
6.【答案】①②③④
【知识点】平行四边形的判定;菱形的判定;矩形的判定;正方形的判定
7.【答案】A
【知识点】平行四边形的判定;菱形的判定;矩形的判定
8.【答案】C
【知识点】平行四边形的性质;菱形的性质;矩形的性质;正方形的性质
9.【答案】B
【知识点】坐标与图形性质;菱形的性质
10.【答案】C
【知识点】线段垂直平分线的性质;等边三角形的判定与性质;勾股定理;菱形的性质
11.【答案】B
【知识点】无理数的估值;正方形的性质
12.【答案】(1)证明:,
在和中,
(2)解:
【知识点】三角形全等及其性质;勾股定理;矩形的性质;三角形全等的判定-AAS
13.【答案】(1)①菱形;②
(2)①12;②
【知识点】勾股定理;菱形的性质;三角形全等的判定-SAS;三角形的中位线定理
14.【答案】(1);(2)
【知识点】负整数指数幂;勾股定理;矩形的性质;求特殊角的三角函数值
15.【答案】(1)
(2)或
(3)点F的坐标为
【知识点】待定系数法求一次函数解析式;勾股定理;菱形的性质;一次函数图象的平移变换
16.【答案】(1)解:连接,利用直尺和圆规作线段的垂直平分线交,于点E,F,则点E,F为所求.如图,
证明如下:设与交于点O,
∵四边形为矩形,
∴,,
∴,
∵是的垂直平分线,
∴,,,
在和中,
,
∴,
∴,
∴,
∴四边形为菱形,
∴点E,F为所求作的点.
(2)解:设菱形的边长为x,则菱形的的周长为,
在中,,,,
由勾股定理得:,
即:,
解得:,
∴菱形的的周长为.
答:菱形的周长为20.
【知识点】线段垂直平分线的性质;勾股定理;菱形的判定;矩形的性质;尺规作图-垂直平分线
17.【答案】
【知识点】平行线的性质;勾股定理;矩形的判定与性质;解直角三角形的其他实际应用
18.【答案】(1)解:∵ABCD是菱形,
∴AC⊥BD,
∴直角△OCD中,OC= (cm)
(2)解:∵CE∥DB,BE∥AC,
∴四边形OBEC为平行四边形,
又∵AC⊥BD,即∠COB=90°,
∴平行四边形OBEC为矩形,
∵OB=0D,
∴S矩形OBEC=OB OC=4×3=12(cm2)
【知识点】菱形的性质;矩形的判定与性质
19.【答案】(1)解:BD=CD.
理由如下:依题意得AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD
(2)解:当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD(三线合一),
∴∠ADB=90°,
∴ AFBD是矩形.
【知识点】全等三角形的判定与性质;矩形的判定
20.【答案】解:赞成小洁的说法, 补充条件: ,
证明如下:
,
四边形ABCD是平行四边形.
又
∴ 平行四边形 是菱形.
【知识点】菱形的判定
21世纪教育网(www.21cnjy.com)
2 / 10
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
