6.3反比例函数的应用（含答案）

中小学教育资源及组卷应用平台
6.3反比例函数的应用
一、填空题
1．某新能源汽车每小时充电3kW h，充满电量需要7h，1kW h的电量可行驶8km，则充满电后平均每天行驶的里程数s（km）与可行驶天数n（天）之间的关系式为　 　．
2．数学实验课上，小明同学用自制“密度计”测量液体的密度．密度计悬浮在不同的液体中时，浸在液体中的高度h（单位：cm）是液体的密度（单位：）的反比例函数，当密度计悬浮在密度为的水中时，，当密度计悬浮在另一种液体中时，，则该液体的密度　 　．
3．长方形的面积为60cm2，如果它的长是ycm，宽是xcm，那么y是x的　 　函数关系，y写成x的关系式是　 　.
4．已知闭合电路的电压为定值，电流I（单位：A ）与电路的电阻R单位：Ω）是反比例函数关系，根据表格 则　 　．
10 2.4 2 1.2
a 50 60 100
5．当灯泡两端电压恒定时，通过灯泡的电流与其电阻成反比例，关于的函数图象如图所示，当电流时，电阻的取值范围是　 　．
6．菱形的面积为12cm2，两条对角线分别为x(cm)和y(cm)，则y关于x的函数表达式为 　 　，当其中一条对角线x=6cm时，另一条对角线y=　 　cm．
二、单选题
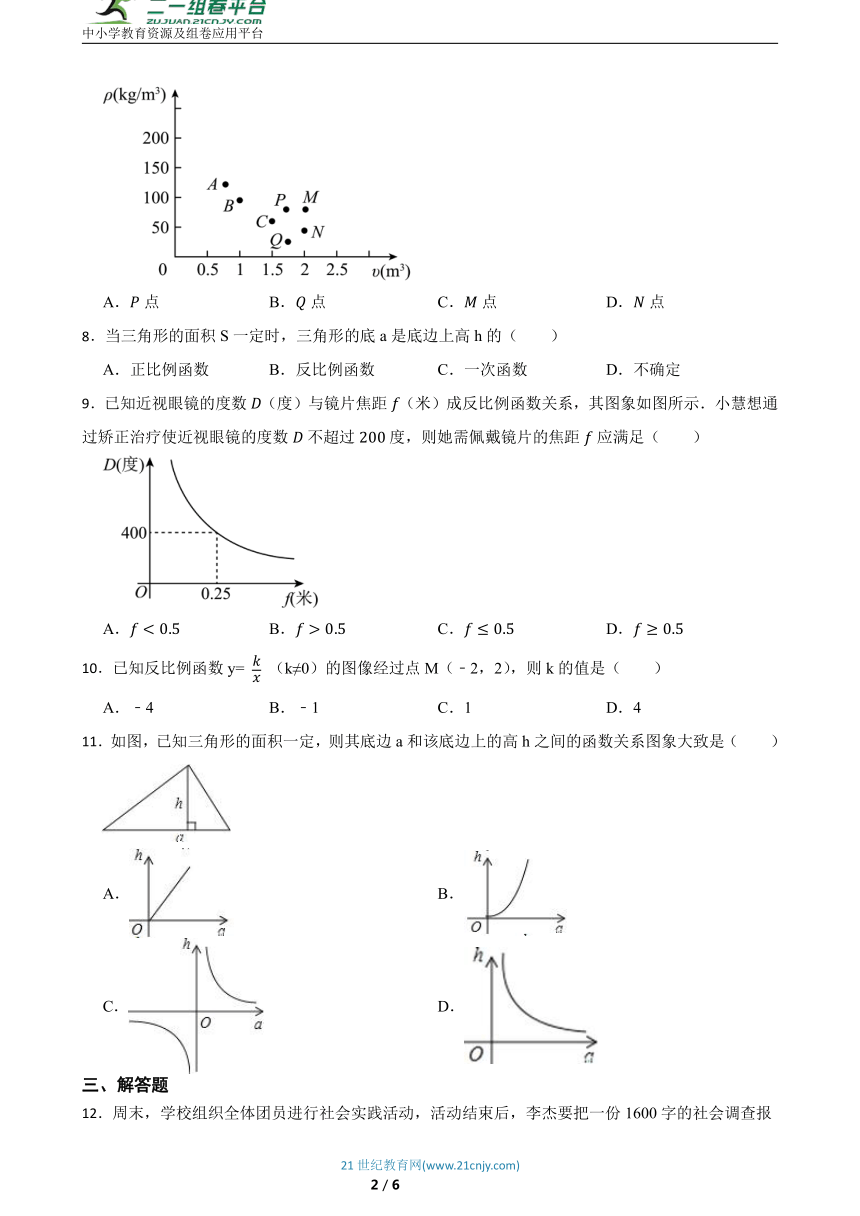
7．在恒温实验室里，有充满一定质量气体的密闭气球，现三次改变气球的体积并测得球内气体的密度，体积与密度的三对对应值分别用右图所示的点、点、点表示，若第四次改变体积，得到体积与密度的对应值可以表示成的点是（　　）
A．点 B．点 C．点 D．点
8．当三角形的面积S一定时，三角形的底a是底边上高h的（　　）
A．正比例函数 B．反比例函数 C．一次函数 D．不确定
9．已知近视眼镜的度数（度）与镜片焦距（米）成反比例函数关系，其图象如图所示．小慧想通过矫正治疗使近视眼镜的度数不超过度，则她需佩戴镜片的焦距应满足（　　）
A． B． C． D．
10．已知反比例函数y= （k≠0）的图像经过点M（﹣2，2），则k的值是（　　）
A．﹣4 B．﹣1 C．1 D．4
11．如图，已知三角形的面积一定，则其底边a和该底边上的高h之间的函数关系图象大致是（　　）
A． B．
C． D．
三、解答题
12．周末，学校组织全体团员进行社会实践活动，活动结束后，李杰要把一份1600字的社会调查报告录入电脑.设他录入文字的速度为字/分，完成录入所需的时间为分钟.
（1）求与之间的函数关系式；
（2）当李杰录入文字的速度为100字/分，完成录入的时间为多少？
四、计算题
13．新冠疫情下的中国在全世界抗疫战斗中全方位领跑．某制药公司生产3支单针疫苗和2支双针疫苗需要19min；生产2支单针疫苗和1支双针疫苗需要11min．
（1）制药公司生产1支单针疫苗和1支双针疫苗各需要多少时间？
（2）小明选择注射双针疫苗，若注射第一针疫苗后，体内抗体浓度y（单位：min/ml）与时间x（单位：天）的函数关系如图所示：疫苗注射后体内抗体浓度首先y与x成一次函数关系，体内抗体到达峰值后，y与x成反比例函数关系．若体内抗体浓度不高于50min/ml时，并且不低于23min/ml，可以打第二针疫苗，刺激记忆细胞增殖分化，产生大量浆细胞而产生更多的抗体．请问：小明可以在哪个时间段内打第二针疫苗？请通过计算说明．
五、作图题
14．王芳同学在一次做电学实验时，记录下电流与电阻的一些对应值，通过描写连线，画出了关于的函数图象如图，求与之间的函数关系式，并求当电阻为时，电流的值是多少．
六、综合题
15．某电厂有5000吨电煤．
（1）求：这些电煤能够使用的天数x(单位：天)与该厂平均每天用煤吨数y(单位：吨)之间的函数关系；
（2）若平均每天用煤200吨，则这批电煤能用多少天？
（3）若该电厂前10天每天用200吨，后因各地用电紧张，每天用电煤300吨，则这批电煤共可用多少天？
16．某空调生产厂的装配车间计划在一段时期内组装一批空调，计划是每天组装的数量y（台/天）与组装的时间x（天）之间的关系如下表：
组装的时间x（天） 30 45 60
每天组装的数量y（台/天） 300 200 150
（1）求y关于x的关系式；
（2）某商场以进货价为每台2500元购进这批空调．调查发现，当销售价为2900元时，平均每天能售出8台；当销售价每降低100元时，平均每天就能多售出4台．商场要想这批空调的销售利润平均每天达到3500元，且让顾客得到最大优惠，每台空调的定价为多少元？
17．一辆汽车匀速通过某段高速公路，所需时间（单位：与行驶速度（单位：）满足函数关系式：，其图象为如图所示的一段曲线，且端点为，．
（1）求与的值；
（2）受天气影响，若行驶速度不得超过，则汽车通过该路段最少需要多长时间？
七、实践探究题
18．综合与实践
如图，某校数学兴趣小组取一根长为的匀质木杆，把细绳绑在木杆的中点处并将其吊起．在中点左侧距离中点处挂一个重的物体，在中点右侧用一个弹簧秤向下拉，使木杆处于水平状态．改变弹簧秤与中点的距离（单位：），观察弹簧秤的示数（单位：）有什么变化，得到下表：
5 10 15 20 25 30 35 40
16
指导老师发现其中有一组数据明显是错误的．
（1）当 时，所对应的的值明显是错误的；
（2）写出与之间的函数关系式，并求当弹簧秤的示数是时，弹簧秤与中点之间的距离．
答案解析部分
1．【答案】
2．【答案】
3．【答案】反比例函数；
4．【答案】12
5．【答案】
6．【答案】y=；4
7．【答案】D
8．【答案】B
9．【答案】D
10．【答案】A
11．【答案】D
12．【答案】（1）解：由题意，得与之间的函数关系式为
（2）解：将字/分代入上式，得（分），
答：完成录入所需的时间为16分钟．
13．【答案】（1）生产1支单针疫苗需要3min；生产1支双针疫苗需要5min；
（2）小明应在打第二针疫苗的时间段为打第一针后的第13天到第27天内．
14．【答案】，当电阻为时，电流的值
15．【答案】（1）解：y＝ .
（2）解：把x＝200代入y＝ ，
得y＝25.
故这批电煤能用25天
（3）解：前10天后还剩下5000－10×200＝3000(吨)电煤，可以用 ＝10(天)，故共可用20天
16．【答案】（1）y关于x的关系式为；
（2）每台空调的定价为2750元．
17．【答案】（1），
（2）汽车通过该路段最少需要
18．【答案】（1）
（2）
21世纪教育网(www.21cnjy.com)
2 / 7