第六章反比例函数（含答案）

中小学教育资源及组卷应用平台
第六章反比例函数
一、单选题
1．已知点，，都在反比例函数的图象上，则的大小关系为（　　）
A． B． C． D．
2．关于反比例函数，下列说法中正确的是（　　）
A．它的图象分在在第二、四象限
B．它的图象过点
C．当时，y的值随x的增大而减小
D．与y轴的交点是
3．下列函数是反比例函数的是（　　）
A． B． C． D．
4．如图所示，一次函数的图象和反比例函数的图象交于A（1，2），B（-2，-1）两点，若，则x的取值范围是 ( )
A．x<1 B．x<-2
C．-21 D．x<-2 或 05．关于函数的图象，下列说法错误的是（　　）
A．经过点
B．当时，随的增大而增大
C．当时，
D．是中心对称图形，且对称中心为原点
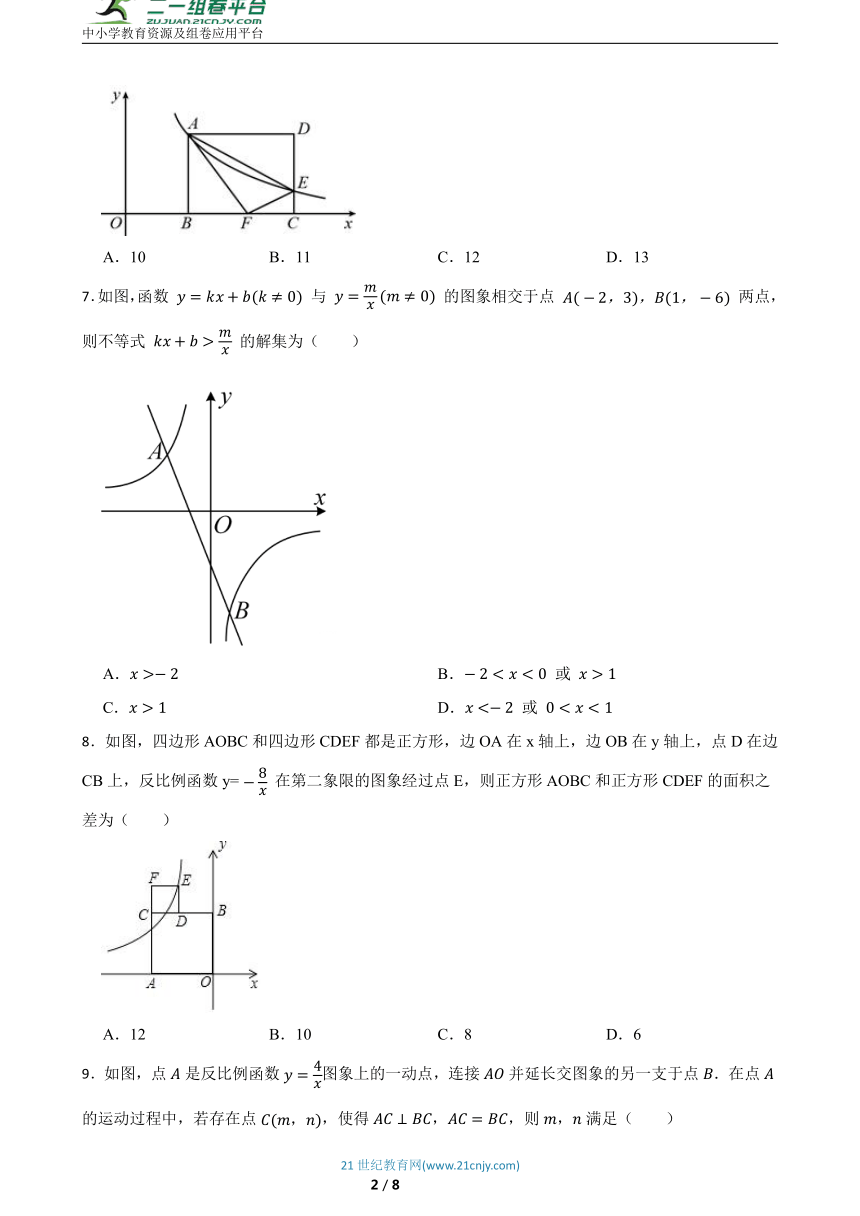
6．如图，已知矩形 的边 在 轴上， ， ，双曲线 与矩形相交于点 ， ，沿 折叠 ，点 恰好落在 上的点 处，则 的值为（　　）
A．10 B．11 C．12 D．13
7．如图，函数 与 的图象相交于点 两点，则不等式 的解集为（　　）
A． B． 或
C． D． 或
8．如图，四边形AOBC和四边形CDEF都是正方形，边OA在x轴上，边OB在y轴上，点D在边CB上，反比例函数y= 在第二象限的图象经过点E，则正方形AOBC和正方形CDEF的面积之差为（　　）
A．12 B．10 C．8 D．6
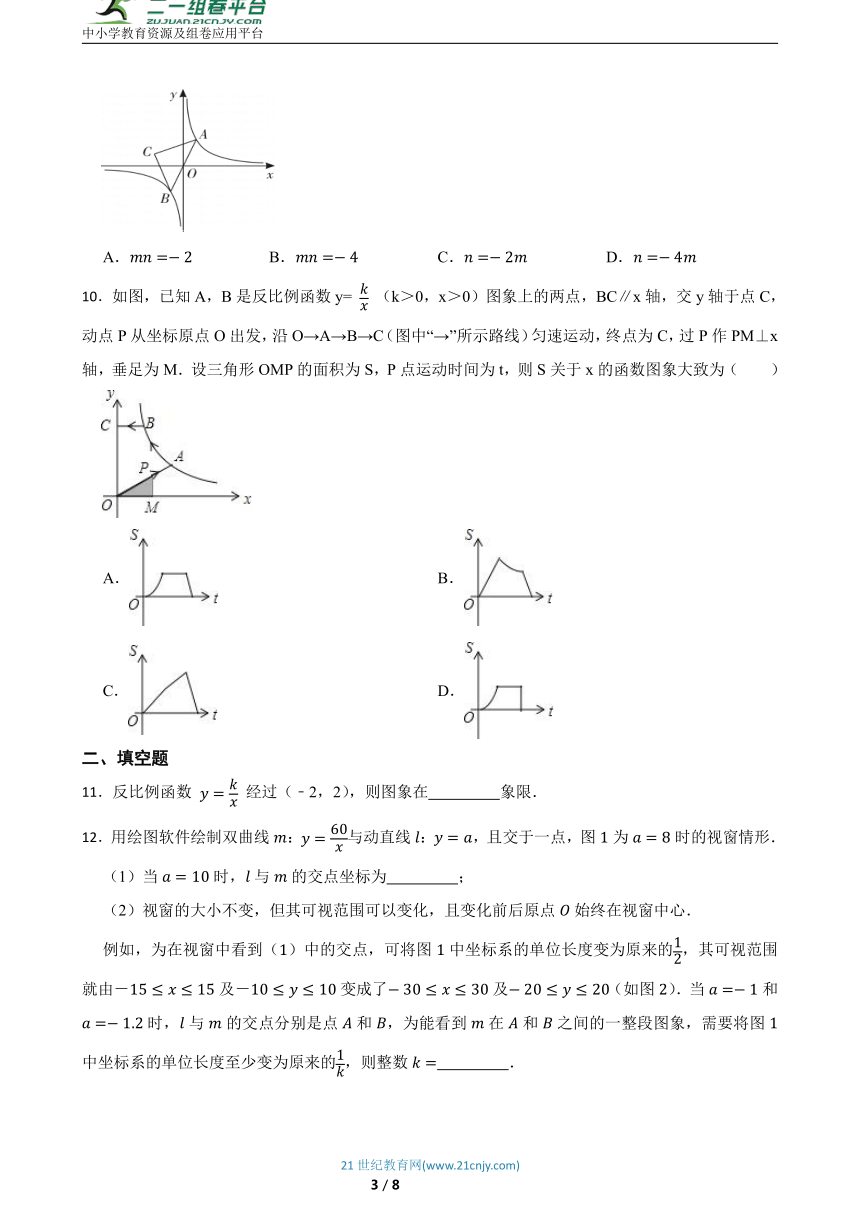
9．如图，点是反比例函数图象上的一动点，连接并延长交图象的另一支于点．在点的运动过程中，若存在点，使得，，则，满足（　　）
A． B． C． D．
10．如图，已知A，B是反比例函数y= （k＞0，x＞0）图象上的两点，BC∥x轴，交y轴于点C，动点P从坐标原点O出发，沿O→A→B→C（图中“→”所示路线）匀速运动，终点为C，过P作PM⊥x轴，垂足为M．设三角形OMP的面积为S，P点运动时间为t，则S关于x的函数图象大致为（　　）
A． B．
C． D．
二、填空题
11．反比例函数 经过（﹣2，2），则图象在　 　象限．
12．用绘图软件绘制双曲线：与动直线：，且交于一点，图为时的视窗情形．
（1）当时，与的交点坐标为　 　；
（2）视窗的大小不变，但其可视范围可以变化，且变化前后原点始终在视窗中心．
例如，为在视窗中看到（）中的交点，可将图中坐标系的单位长度变为原来的，其可视范围就由－及－变成了及（如图）．当和时，与的交点分别是点和，为能看到在和之间的一整段图象，需要将图中坐标系的单位长度至少变为原来的，则整数　 　．
13．若反比例函数的图象经过第二、四象限，则m的取值范围是 　 　．
14．如图，反比例函数的图象与直线相交于A，B两点，过点作轴于，连接AC，则的面积是　 　.
15．在平面直角坐标系中，点A（﹣2，1），B（3，2），C（﹣6，m）分别在三个不同的象限.若反比例函数y＝ （k≠0）的图象经过其中两点，则m的值为　 　.
16．如图，矩形 的顶点A在y轴的正半轴上，顶点C在x轴的正半轴上，反比例函数 在第一象限内的图象分别与边 、 相交于点D、E.连结 ， ，恰有 ， ，若 ，则k的值是　 　.
三、计算题
17．已知反比例函数与一次函数的图象交于点和点．
（1）求这两个函数的表达式；
（2）在同一坐标系中画出上述两个函数图象，观察图象：当时，直接写出自变量x的取值范围．
18．如图，在平面直角坐标系中，正比例函数的图象与反比例函数的图象都经过点．
（1）求反比例函数解析式；
（2）若这两个函数图象的另一个交点为C，点B在x轴上，且，求点B的坐标；
（3）若点在该反比例函数图象上，且它到x轴距离小于3，请根据图象直接写出m的取值范围．
19．一次函数 与反比例函数的图象交于A，B两点，与x轴交于点C，其中．
（1）求反比例函数表达式；
（2）结合图象，直接写出时，x的取值范围；
（3）若点P在x轴上，且是直角三角形，求点P的坐标．
四、解答题
20．为了预防流感，某学校在休息天用药熏消毒法对教室进行消毒．已知药物释效过程中，室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例；药物释放完毕后，y与x成反比例，如图所示．根据图中提供的信息，解答下列问题：
（1）写出从药物释放开始，y与x之间的两个函数关系式及相应的自变量取值范围；
（2）据测定，当空气中每立方米的含药量降低到0.9毫克以下时，学生方可进入教室，那么从药物释放开始，至少需要经过多少小时后，学生才能进入教室
21．已知反比例函数的图象位于第二、四象限．
（1）求的取值范围；
（2）若点是该反比例函数图象上的两点，试比较函数值的大小．
22．已知反比例函数的图象位于第一、三象限．
（1）求的取值范围；
（2）若，反比例函数的图象过点，求的值．
23．如图，在平面直角坐标系中，将一块等腰直角三角板放在第二象限，斜靠在两坐标轴上，点坐标为，点的坐标为，一次函数的图象经过点，，反比例函数图象也经过点．
（1）分别求出一次函数和反比例函数的解析式；
（2）直接写出当时，的解集；
（3）点是平面直角坐标系上任意一点，点是轴上一动点，当以点A、C、P、Q为顶点的四边形是菱形时，请直接写出点的坐标．
答案解析部分
1．【答案】B
2．【答案】C
3．【答案】B
4．【答案】D
5．【答案】C
6．【答案】C
7．【答案】D
8．【答案】C
9．【答案】B
10．【答案】A
11．【答案】二、四
12．【答案】；
13．【答案】
14．【答案】2
15．【答案】-1
16．【答案】
17．【答案】（1）反比例函数的表达式为 ，一次函数的表达式为
（2） 或
18．【答案】（1）
（2）或
（3）或
19．【答案】（1）
（2）
（3）或
20．【答案】（1）（），（）；（2）2小时．
21．【答案】（1）
（2）
22．【答案】（1）解：由题意，k﹣4＞0，
解得：k＞4；
（2）解：∵k＝6，
∴反比例函数的表达式为，
把点A（2，m）代入，得：，
∴m＝1．
23．【答案】（1），
（2）
（3）点坐标为或或或
21世纪教育网(www.21cnjy.com)
2 / 8