第六章反比例函数【培优】（含答案）

中小学教育资源及组卷应用平台
第六章反比例函数【培优】
一、填空题
1．（2017·中山模拟）反比例函数y= 的图象经过点（2，3），则k=　 　．
2．（2023九上·新城月考）如图，已知双曲线经过直角三角形斜边的中点D，且与直角边相交于点C．若点B的坐标为，则的面积为　 　．
3．（2024八下·射洪期中）在函数的图象上有三个点的坐标分别为、、，则、、的大小关系是　 　．
4．（2023·惠民模拟）如图，四边形OABC是平行四边形，点O是坐标原点，点C在y轴上，点B在反比例函数y=（x＞0）的图象上，点A在反比例函数y=（x＞0）的图象上，若平行四边形OABC的面积是7，则k=　 　．
5．（2023·秀洲模拟）已知点 在反比例函数 的图象上，且 .则 的取值范围为　 　.
6．（2023·兴宁模拟）如图，点，在反比例函数的图象上，延长与轴负半轴交于点，连接，若点是的中点，的面积等于，则的值为　 　．
二、单选题
7．（2021·顺城模拟）下列函数中，y是x的反比例函数的是（　　）
A． B． C． D．
8．（2024九下·万载月考）如图，点A在反比例函数的图象上，点B在反比例函数的图象上，连接，与y轴交于点C，且轴，D是x轴正半轴上一点．连接，，则的面积为（　　）
A．2 B．3 C．4 D．6
9．（2023九上·平山月考） 反比例函数的图象在（　　）
A．第一、三象限 B．第二、四象限
C．第一、二象限 D．第三、四象限
10．（2020八下·邓州期中）如果反比例函数y＝ 的图象在每个象限内，y随着x的增大而增大，则m的最小整数值为（　　）
A．﹣1 B．0 C．1 D．2
11．（2023九上·义乌开学考）以下四个点中，不在反比例函数图象上的是（　　）
A． B． C． D．
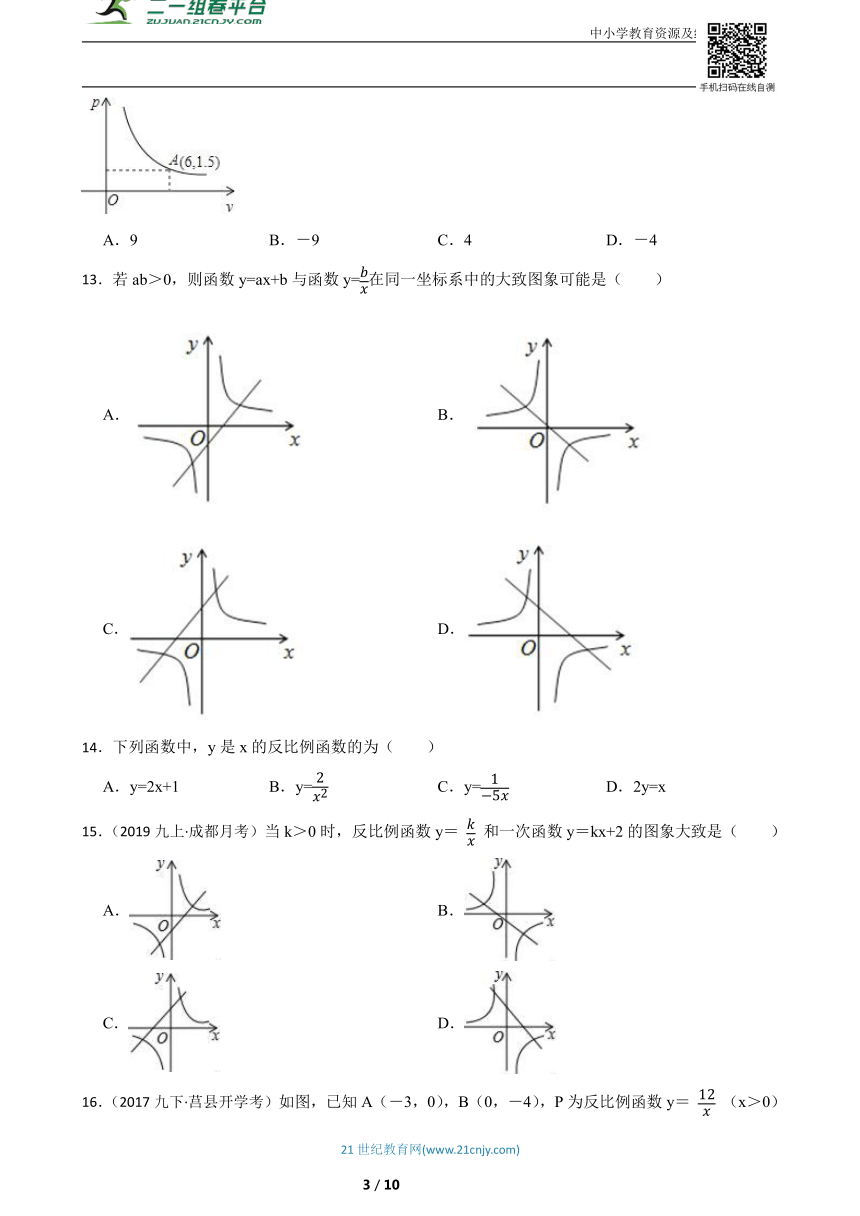
12．在一个可以改变体积的密闭容器内装有一定质量的某种气体，当改变容器的体积时，气体的密度也会随之改变，密度ρ（单位：kg/m3）与体积v（单位：m3）满足函数关系式ρ=（k为常数，k≠0）其图象如图所示，则k的值为(　　）
A．9 B．－9 C．4 D．－4
13．若ab＞0，则函数y=ax+b与函数y=在同一坐标系中的大致图象可能是（　　）
A． B．
C． D．
14．下列函数中，y是x的反比例函数的为（　　）
A．y=2x+1 B．y= C．y= D．2y=x
15．（2019九上·成都月考）当k＞0时，反比例函数y＝ 和一次函数y＝kx+2的图象大致是（　　）
A． B．
C． D．
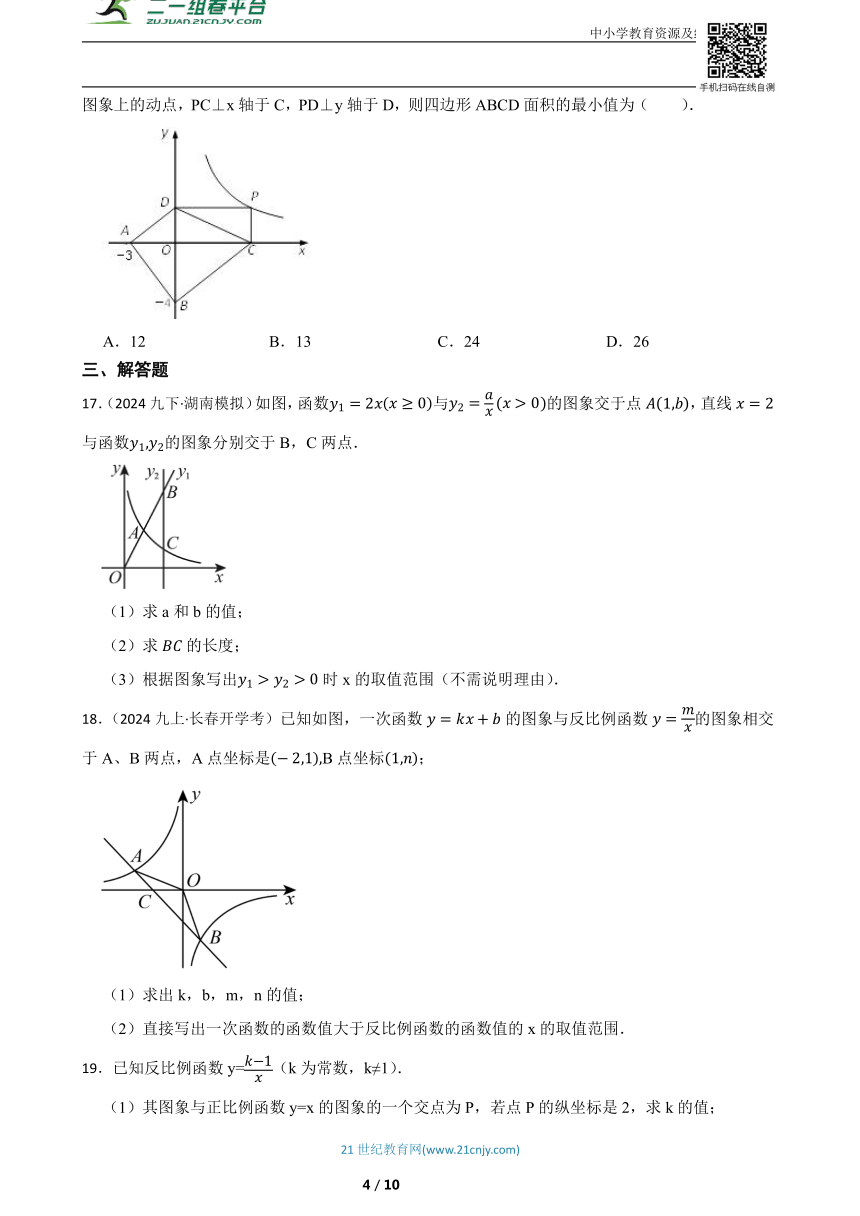
16．（2017九下·莒县开学考）如图，已知A（－3，0），B（0，－4），P为反比例函数y＝ （x＞0）图象上的动点，PC⊥x轴于C，PD⊥y轴于D，则四边形ABCD面积的最小值为（　　）．
A．12 B．13 C．24 D．26
三、解答题
17．（2024九下·湖南模拟）如图，函数与的图象交于点，直线与函数的图象分别交于B，C两点．
（1）求a和b的值；
（2）求的长度；
（3）根据图象写出时x的取值范围（不需说明理由）．
18．（2024九上·长春开学考）已知如图，一次函数的图象与反比例函数的图象相交于A、B两点，A点坐标是B点坐标；
（1）求出k，b，m，n的值；
（2）直接写出一次函数的函数值大于反比例函数的函数值的x的取值范围．
19．已知反比例函数y=（k为常数，k≠1）．
（1）其图象与正比例函数y=x的图象的一个交点为P，若点P的纵坐标是2，求k的值；
（2）若在其图象的每一支上，y随x的增大而减小，求k的取值范围；
（3）若其图象的一支位于第二象限，在这一支上任取两点A（x1、x2）、B（x2、y2），当y1＞y2时，试比较x1与x2的大小；
（4）若在其图象上任取一点，向x轴和y轴作垂线，若所得矩形面积为6，求k的值．
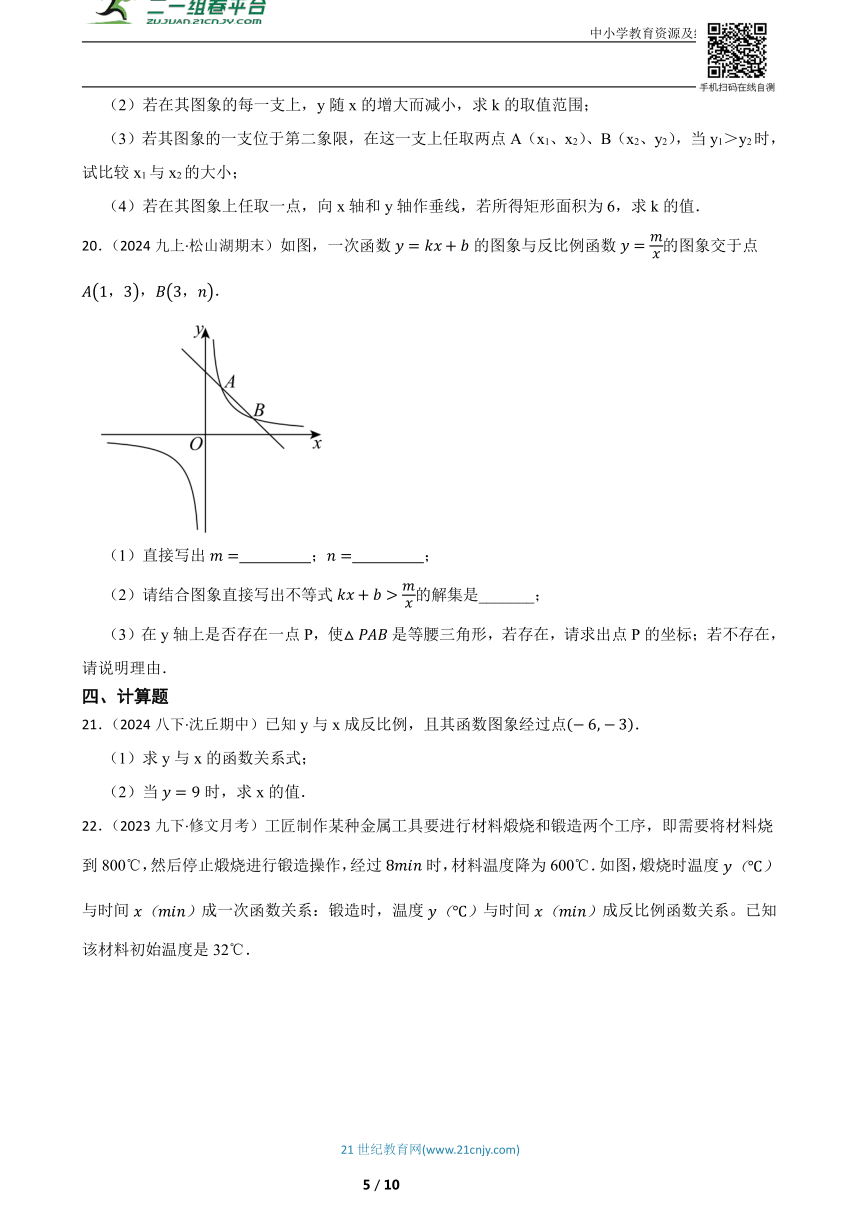
20．（2024九上·松山湖期末）如图，一次函数的图象与反比例函数的图象交于点，．
（1）直接写出　 　；　 　；
（2）请结合图象直接写出不等式的解集是_______；
（3）在y轴上是否存在一点P，使是等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．
四、计算题
21．（2024八下·沈丘期中）已知y与x成反比例，且其函数图象经过点．
（1）求y与x的函数关系式；
（2）当时，求x的值．
22．（2023九下·修文月考）工匠制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800℃，然后停止煅烧进行锻造操作，经过时，材料温度降为600℃．如图，煅烧时温度与时间成一次函数关系：锻造时，温度与时间成反比例函数关系。已知该材料初始温度是32℃．
（1）分别求出材料煅烧和锻造时与的函数关系式，并且写出自变量的取值范围；
（2）根据工艺要求，当材料温度低于400℃时，须停止操作．那么锻造的操作时间最多有多长？．
（3）如果加工每个零件需要锻造12分钟，并且当材料温度低于400℃时，需要重新煅烧．通过计算说明加工第一个零件，一共需要多少分钟．
23．（2024八下·新吴期末）如图，已知在平面直角坐标系中，其中，，且、、．
（1）求点坐标；
（2）将沿轴的正方向平移，在第一象限内、两点的对应点、正好落在某反比例函数图象上．请求出这个反比例函数和此时的直线的解析式；
（3）在（2）的条件下，直线交轴于点．若存在轴上的点和反比例函数图象上的点，使得由、、、四点构成的四边形是平行四边形．请直接写出点和点的坐标；若不存在满足题意的平行四边形，请说明理由．
答案解析部分
1．【答案】7
【知识点】反比例函数图象上点的坐标特征
2．【答案】3
【知识点】待定系数法求反比例函数解析式
3．【答案】
【知识点】反比例函数的性质
4．【答案】-4
【知识点】反比例函数系数k的几何意义；平行四边形的性质
5．【答案】-2＜m＜2
【知识点】反比例函数的性质
6．【答案】-6
【知识点】反比例函数的性质
7．【答案】A
【知识点】反比例函数的概念
8．【答案】B
【知识点】反比例函数系数k的几何意义
9．【答案】A
【知识点】反比例函数的图象
10．【答案】C
【知识点】反比例函数的性质
11．【答案】D
【知识点】反比例函数的图象
12．【答案】A
【知识点】反比例函数的实际应用
13．【答案】C
【知识点】反比例函数的图象
14．【答案】C
【知识点】反比例函数的概念
15．【答案】C
【知识点】反比例函数的性质；一次函数图象、性质与系数的关系
16．【答案】C
【知识点】反比例函数系数k的几何意义
17．【答案】（1），
（2）
（3）
【知识点】待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
18．【答案】（1），，
（2）或
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
19．【答案】解：（1）由题意，设点P的坐标为（m，2）
∵点P在正比例函数y=x的图象上，
∴2=m，即m=2．
∴点P的坐标为（2，2）．
∵点P在反比例函数y=的图象上，
∴2=，解得k=5．
（2）∵在反比例函数y=图象的每一支上，y随x的增大而减小，
∴k﹣1＞0，解得k＞1．
（3）∵反比例函数y=图象的一支位于第二象限，
∴在该函数图象的每一支上，y随x的增大而增大．
∵点A（x1，y1）与点B（x2，y2）在该函数的第二象限的图象上，且y1＞y2，
∴x1＞x2．
（4）∵在其图象上任取一点，向两坐标轴作垂线，得到的矩形为6，
∴|k|=6，
解得：k=±6．
【知识点】反比例函数的性质；反比例函数系数k的几何意义；反比例函数图象上点的坐标特征
20．【答案】（1）3；1
（2）或；
（3）解：在y轴上存在一点P，使是等腰三角形；
理由如下：
∵，，
∴，
设点P坐标为，
①当时，得：，
解得：或，
此时点P坐标为或；
②当时，得：，此时无解；
③当时，得：，
解得：，
此时点P坐标为，
综上，点P的坐标为或或．
【知识点】待定系数法求反比例函数解析式；反比例函数与一次函数的交点问题
21．【答案】（1）
（2）
【知识点】待定系数法求反比例函数解析式
22．【答案】（1），；（2）锻造一次操作时间为6分钟；（3）加工第一个零件一共需要分钟．
【知识点】反比例函数的实际应用；一次函数的其他应用
23．【答案】（1）
（2）反比例函数解析式为，此时的直线的解析式
（3）存在点、点使得、、、四个点构成的四边形是平行四边形，点的坐标为，点的坐标为或点的坐标为，点的坐标为
【知识点】待定系数法求一次函数解析式；待定系数法求反比例函数解析式；平行四边形的性质
21世纪教育网(www.21cnjy.com)
1 / 10