浙教版第四章4.4平行四边形的判定(2)
文档属性
| 名称 | 浙教版第四章4.4平行四边形的判定(2) |

|
|
| 格式 | zip | ||
| 文件大小 | 244.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-25 00:00:00 | ||
图片预览




文档简介
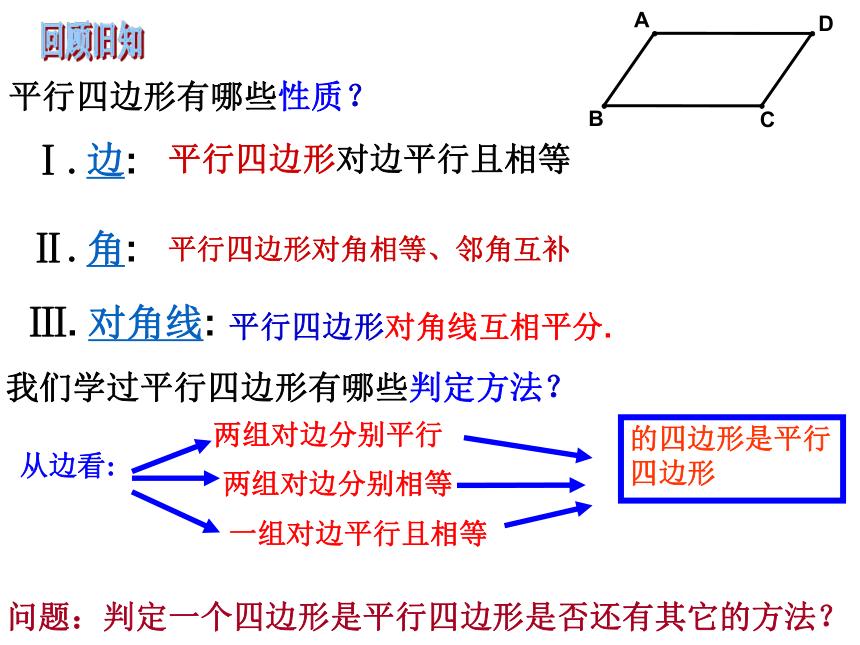
课件15张PPT。4.4平行四边形的判定定理(2)回顾旧知平行四边形有哪些性质? 平行四边形对角线互相平分.我们学过平行四边形有哪些判定方法? 从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 问题:判定一个四边形是平行四边形是否还有其它的方法?平行四边形对边平行且相等平行四边形对角相等、邻角互补 学习了平行四边形后,小明回家用细木棒钉制了一个。第二天,小明拿着自己动手做的平行四边形向同学们展示。
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙情境引入 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
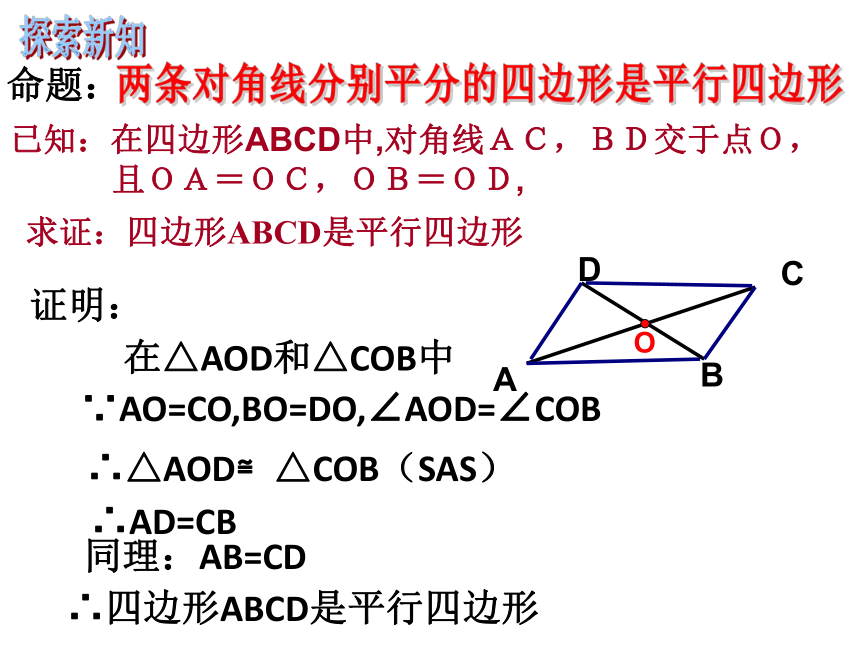
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?探索新知两条对角线分别平分的四边形是平行四边形OBD已知:在四边形ABCD中,对角线AC,BD交于点O,
且OA=OC,OB=OD,求证:四边形ABCD是平行四边形命题:证明:在△AOD和△COB中∵AO=CO,BO=DO,∠AOD=∠COB∴△AOD≌△COB(SAS)∴AD=CB同理:AB=CD∴四边形ABCD是平行四边形平行四边形判定定理:
两条对角线互相平分的四边形是平行四边形.几何语言:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形
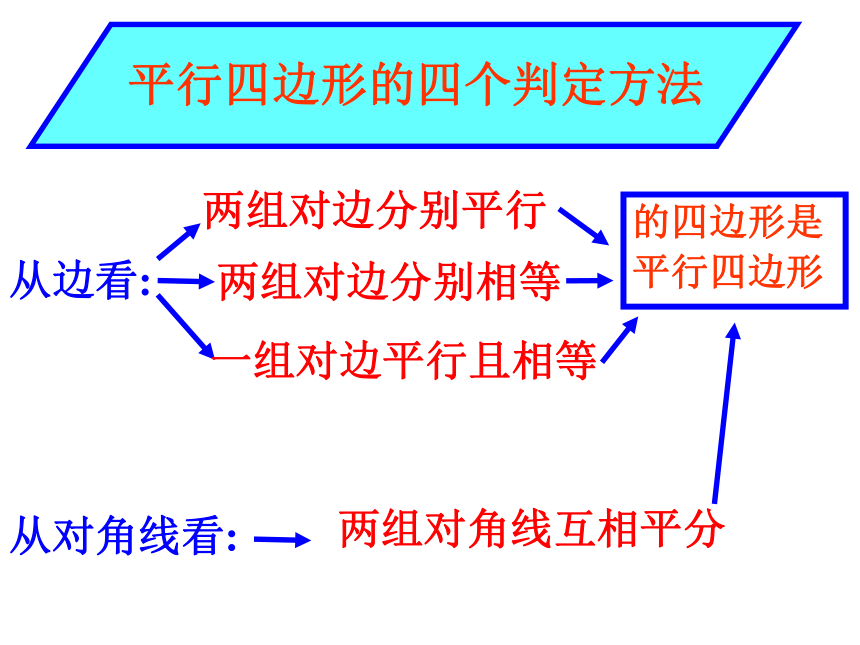
从边看: 平行四边形的四个判定方法两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形
从对角线看: 两组对角线互相平分 如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,____,则得 ABCD补充一个合适的条件结论成立:例1 已知:如图,在 ABCD中,E,F是对角线BD
上的两点,且BE=DF.
求证:四边形AECF是平行四边形O讨论:根据现有条件,说说你准备选用哪种方法证明?
大概的步骤是怎样的?证明:在 ABCD中连结AC交BD于点O∵对角线AC,BD交于点O ∴ AO=CO BO=DO ∵BE=DF ∴BO-BE=DO-DF即EO=FO∴四边形AECF是平行四边形例题讲解O证明:连结AC,交BD于点O∵AB∥CD∴∠ABE=∠CDF又∵∠BAE=∠CDF,AB=CD∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF,即EO=FO∴四边形AECF是平行四边形变式训练巩固练习2.已知线段a,b,∠α(如图),请用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a,b,两条对角线的夹角等于∠αα3.如图四边形ABCD是不是平行四边形?请给出证明.ABCDxyo-1-111∴O平分AC,O平分BD连接对角线AC,BD则有
OA=OC,OB=OD∴四边形ABCD是平行四边形 任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现。发现:三角形一条边上的中线的2倍小于另两条边的和。E已知:如图,AD是⊿ABC的中线,求证:2ADAE,∴AB+AC>2AD,即2AD
小辉却问:你凭什么确定这四边形就是平行四边形呢?
大家都困惑了……请你帮忙情境引入 小丽却说:“我可以不用任何作图工具,只要两条细绳就能判断它是不是平行四边形。”
只见小丽用两条细绳做四边形的对角线,并在两条对角线的交点处作了个记号。然后分别把两条对角线沿记号点对折,发现它们被记号点分成的两段线段都能重合,小丽高兴地说:“这的确是个平行四边形!”你认为小丽的做法有根据吗?探索新知两条对角线分别平分的四边形是平行四边形OBD已知:在四边形ABCD中,对角线AC,BD交于点O,
且OA=OC,OB=OD,求证:四边形ABCD是平行四边形命题:证明:在△AOD和△COB中∵AO=CO,BO=DO,∠AOD=∠COB∴△AOD≌△COB(SAS)∴AD=CB同理:AB=CD∴四边形ABCD是平行四边形平行四边形判定定理:
两条对角线互相平分的四边形是平行四边形.几何语言:
∵OA=OC,OB=OD,
∴四边形ABCD是平行四边形
从边看: 平行四边形的四个判定方法两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形
从对角线看: 两组对角线互相平分 如图,四边形ABCD对角线AC、BD相交于点O
⑴若AB∥CD,______,则得 ABCD;
⑵若AB=CD,______,则得 ABCD;
⑶若AC=8,BD=10,AO=4,____,则得 ABCD补充一个合适的条件结论成立:例1 已知:如图,在 ABCD中,E,F是对角线BD
上的两点,且BE=DF.
求证:四边形AECF是平行四边形O讨论:根据现有条件,说说你准备选用哪种方法证明?
大概的步骤是怎样的?证明:在 ABCD中连结AC交BD于点O∵对角线AC,BD交于点O ∴ AO=CO BO=DO ∵BE=DF ∴BO-BE=DO-DF即EO=FO∴四边形AECF是平行四边形例题讲解O证明:连结AC,交BD于点O∵AB∥CD∴∠ABE=∠CDF又∵∠BAE=∠CDF,AB=CD∴△ABE≌△CDF∴BE=DF∴BO-BE=DO-DF,即EO=FO∴四边形AECF是平行四边形变式训练巩固练习2.已知线段a,b,∠α(如图),请用直尺和圆规作一个平行四边形,使它的两条对角线长分别等于线段a,b,两条对角线的夹角等于∠αα3.如图四边形ABCD是不是平行四边形?请给出证明.ABCDxyo-1-111∴O平分AC,O平分BD连接对角线AC,BD则有
OA=OC,OB=OD∴四边形ABCD是平行四边形 任意画一个三角形和三角形一边上的中线。比较这条中线的二倍与三角形另外两边的和的大小,你发现了什么?再画几个三角形试一试,你发现的规律仍然成立吗?试证明你的发现。发现:三角形一条边上的中线的2倍小于另两条边的和。E已知:如图,AD是⊿ABC的中线,求证:2AD
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
